多介質工況下液壓挖掘機斗桿動態特性分析

吳玉文，呂彭民，向清怡

1陜西工業職業技術學院機械工程學院 陜西咸陽 712000

2長安大學工程機械學院 陜西西安 710064

液 壓挖掘機的工作環境惡劣，工作裝置上的負荷也非常復雜，因此，工作裝置的疲勞性能直接影響液壓挖掘機的使用壽命和工作效率[1]。斗桿是液壓挖掘機最主要的工作裝置之一，研究其實際挖掘過程的動態特征十分關鍵。在以往研究中，經常采用的方法是基于虛擬樣機的動力學仿真[2-3]。S.?alinic 等人[4]給出了剛性和柔性地基條件下的液壓挖掘機運動微分凱恩方程，該方程適用于挖掘過程動力學分析。任志貴等人[5]通過試驗測得各組液壓缸壓力和位移數據后，計算出了各鉸接點的動載荷，進而對工作裝置零部件進行了瞬態分析。姜濤等人[6]通過實測到的各液壓缸壓力和位移的時域變化曲線，結合模型，得到挖掘機動臂各鉸點載荷時域譜，進而進行疲勞分析。上述文獻中，液壓挖掘機工作裝置的各鉸點載荷的計算理論上較為準確，但是部分文獻缺乏真實試驗數據的支撐和驗證。即使存在試驗過程，但試驗介質較為單一且近似理想，代表性不強。

筆者主要依托國家科技支撐計劃項目，在液壓挖掘機 4 種真實介質下進行實際挖掘，實測了工作裝置各組液壓缸的壓力和位移數據，從而計算出了斗桿各鉸點的載荷時間歷程 (動載荷)，進而對斗桿進行了瞬態動力學分析。分析結果與實測的大應力位置的應力時間歷程基本一致，證明瞬態動力學可用于斗桿動態特性的分析。

1 瞬態動力學理論

瞬態動力學分析是動力學的一部分，是研究變約束下結構動力響應的技術[7]，可以應用于分析承受各種沖擊載荷的結構和承受各種隨時間變化載荷的結構。液壓挖掘機在挖掘過程中，工作裝置承受的載荷復雜多變，滿足瞬態動力學的應用條件。非線性瞬態動力學的控制方程為

式中：M為結構質量矩陣；C為構阻尼矩陣；K為結構剛性矩陣；F為結構外載荷矢量矩陣；為節點加速度；為節點速度；u為節點位移矢量；F(t) 為作用力。

求解上述方程，可以用直接積分法 (隱式積分、顯式積分) 或者模態疊加法。筆者采用隱式積分法中的完全法就可以解決非線性問題，且適用于施加各種類型的載荷。在考慮慣性力、阻尼力的條件下，在任何給定的時間點，將方程轉換為一系列的靜態平衡方程，而施加在各鉸點的動載荷的準確性是保證瞬態動力學分析可靠的基本條件。向清怡等人[8]通過試驗研究發現，采用基于液壓缸壓力的間接測量法獲取工作裝置鉸點載荷，可以滿足工程需要。

2 液壓缸壓力、位移及大應力點測試

本文所用試驗樣機的技術參數如表 1 所列。斗桿材料為 Q345，其屈服極限為 345 MPa。液壓挖掘機的挖掘過程分為挖掘、提升回轉、卸載和空斗返回 4 個階段[8]。參考標準[9-10]中的規定，確定 4 種工作介質為Ⅰ類松散土，Ⅱ類原生土，Ⅲ類壓實的含小石塊黏土，Ⅳ類石塊、粗卵石或含石塊的黏土。利用壓力傳感器、位移傳感器分別測量液壓缸壓力和位移，并由具有 8 個 AD24 位動態采集通道、采樣率為 200 ks/s串行了的 DEWE-43 數據采集器采集數據。由電阻應變片測量大應力點的應變，由DEWE-2601 動態應變測試儀采集數據。斗桿應變片粘貼位置以及應變片 2的具體位置如圖 1 所示，試驗現場如圖 2 所示。采集到信號后，進行如去除零漂、去除噪聲和去除奇異值的處理。另外，試驗得到的是應變片應變時間歷程信號，還應轉化為應力時間歷程信號。其中，應變片處測點的當量應力σY4根據第四強度理論計算。

表1 某中型液壓挖掘機試驗樣機技術參數Tab.1 Technical parameters of a medium-sized hydraulic excavator

圖1 應變片粘貼位置Fig.1 Location of strain gauge

圖2 試驗現場Fig.2 Test field

基于達朗貝爾動靜法原理，在考慮鉸點力、慣性力和重力的條件下，求解動載荷，具體步驟在文獻[5，8] 中已經給出。另外，為了提升瞬態動力學分析的準確性，動載荷應分解到斗桿局部坐標系下，其水平分力與斗桿局部坐標系x軸 (鉸點A、E連線) 平行。其中，Ⅰ類介質下動臂與斗桿的鉸點A的動載荷變化曲線如圖 3 所示，FAx為水平分力，FAy為豎直分力。

圖3 Ⅰ類介質下動臂與斗桿鉸點 A 的動載荷變化曲線Fig.3 Variation curves of dynamic load at hinge point A of boom and bucket rod in medium I mode

3 斗桿瞬態動力學分析

ANSYS 是美國 ANSYS 公司研發的有限元分析軟件，通過 APDL 語言可以進行二次開發，設計形成具有特定功能的分析模塊。為了更高效地進行分析，基于 VB 對 ANSYS 進行了二次開發，制作了瞬態動力學分析模塊，如圖 4 所示。

圖4 瞬態動力學分析模塊Fig.4 Transient dynamics analysis module

在建立參數化模型時，根據斗桿特點對其結構進行簡化，忽略螺紋孔、運輸吊耳等一些對結構強度影響很小的特征，且焊縫連續，材料與母材相同。為了提高計算精度，選用高階單元 Solid187 單元。基于單元類型及斗桿實際結構，選用自由網格劃分方式。

在約束和加載時，應注意以下幾個方面：

(1) 要在 5 個鉸點的中心建立結構質點 (選用六自由度結構質點 Mass21 單元)，并使鉸孔內表面形成剛性區；

(2) 約束與加載均在結構質點上，使其可以傳導到鉸孔上；

(3) 瞬態動力學分析時，約束方式的選擇也較為重要，在進行了多種約束方式的對比后發現，在鉸點A全約束時，仿真值與實測值更為一致；

(4) 鉸點力實際上是載荷時間歷程，在ANSYS加載鉸點力，最方便的方式就是將鉸點力數據賦值給 Table 表，形成表載荷 (第 1 列是時間，第2 列是力)；

(5) 在進行瞬態動力學分析時，積分步長設定為與動載荷頻率一致，即20 Hz，分析時間與實測采樣時間范圍一致。

4 仿真與測試對比分析

圖5 給出了Ⅰ類介質下各測點瞬態動力學仿真值與實測值的差異。通過對比發現，仿真值與實測值變化規律基本一致。應變片 1 處仿真值與實測值的相關系數為 0.983 026，差值的平均數為 0.797 MPa，標準差為 6.137 5；應變片 2 處仿真值與實測值的相關系數為 0.931 926，差值的平均數為 3.11 MPa，標準差為7.251 2。由于距離應變片 1 較近的鉸點B的約束形式更接近實際，因此應變片 1 處仿真值與實測值更為接近，其差值的標準差也更小。繼續對比其他介質下兩者的差值，Ⅲ類介質下應變片 1 處仿真值與實測值的相關系數為 0.944 115，差值的平均數為 1.26 MPa，標準差為 6.514 7。

圖5 Ⅰ類介質下各測點仿真值與實測值對比Fig.5 Comparison of simulation results and test results at various test points in medium I mode

通過數值比對發現，仿真值與實測值相關性都較高，證明瞬態動力學仿真結果可信，也證明了有限元模型建立和相關處理的合理性。另外，仿真值比實測值波動小，其原因在于，瞬態動力學分析時施加的動載荷，其計算信號經過了去除零漂、去除噪聲等處理，更為穩定。

對 4 種介質下液壓挖掘機一個挖掘循環的多個時刻的斗桿應力云圖進行觀察。在挖掘階段，斗桿應力較大的位置在動臂與斗桿鉸點右側和下蓋板靠近動臂與斗桿鉸點處。在提升回轉階段，在耳板前部位置和上蓋板中部斗桿應力較大。圖 6 給出了Ⅰ類介質下在提升回轉階段t=7 s 時斗桿應力云圖，應力最大值為55.7 MPa，而該時刻應變片 1、2 處實測值均未超過20 MPa，說明僅靠應變片實測很難檢測到最大應力位置。瞬態動力學分析結果可以觀察任意時刻斗桿的應力分布，對斗桿的設計改進有重要的意義。

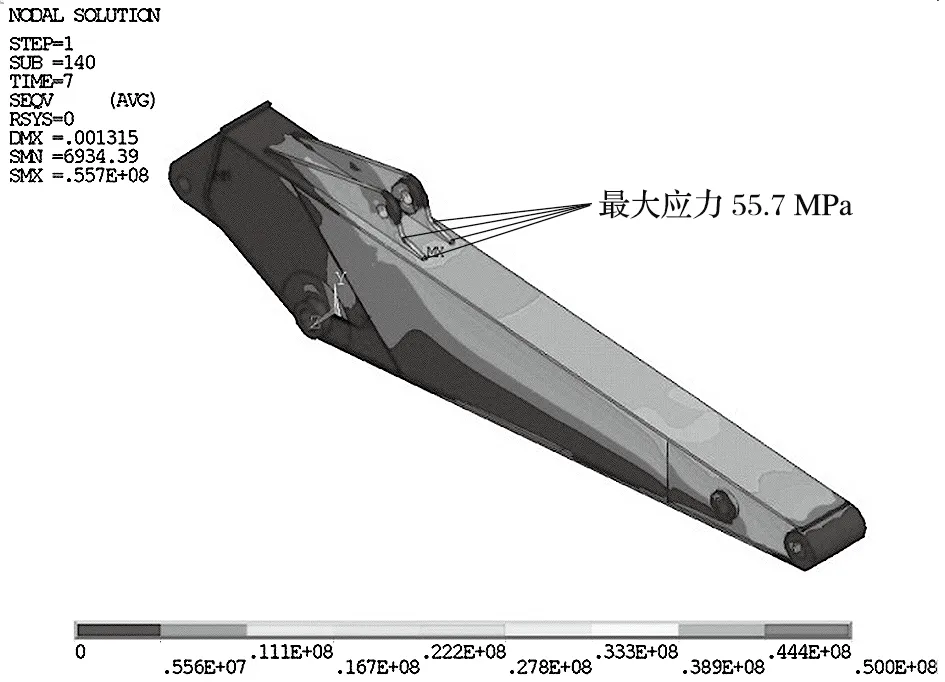
圖6 Ⅰ類介質下在提升回轉階段 t=7 s 時斗桿應力云圖Fig.6 Stress contours of bucket rod at t =7 s of hoisting and rotating stage in medium I mode

5 結論

基于瞬態動力學對液壓挖掘機斗桿進行了動態特性分析，得出了以下結論：

(1) 建立合適的有限元模型，并施加正確的約束條件，可以使得瞬態動力學分析結果與實測結果相關系數達到 0.9 以上。另外，瞬態動力學分析時施加在鉸點的動載荷要準確，該動載荷可以用實測液壓缸壓力和位移后計算獲得。

(2) 實地挖掘試驗中應變片粘貼位置有限，且由于挖掘過程是動態的，斗桿危險位置難以判斷，而瞬態動力學分析結果可以顯示斗桿在任意時刻、任意點位的力學特性。根據該結果，不僅能夠判別實際挖掘過程中的斗桿動應力分布規律和危險點位置，還可以獲得試驗中未粘貼應變片位置的應力時間歷程，為下一步研究提供可信的數據。

(3) 本研究所提的有限元模型建立、動載荷獲取與分解、瞬態動力學分析等方法為研究斗桿及其他工程機械工作裝置類似的關鍵零部件的動態特性提供了思路，也為其后續的設計改進提供了依據。