穩中見變務實創新 題簡義豐培能選賢*
?四川省雙流中學 鄧 明 趙一凡 曹軍才
1 試卷分析
2022年全國甲卷(理科)試卷落實高考改革的總體要求,貫徹德智體美勞全面發展的教育方針,聚焦核心素養,突出閱讀理解、信息整理、語言表達、批判性思維四項關鍵能力的考查,體現了高考數學的科學選拔功能和全面育人導向作用.試題體現以下特點.
1.1 構建豐富情境,發揮育人功能
1.1.1 統計圖表——創設生活情境
如第2題考查統計圖表.統計圖表在生產與生活中應用非常廣泛,前些年是高考熱點,沉寂兩年之后,又出現在了高考試卷中.高考對統計圖表的考查不局限于頻率分布直方圖、莖葉圖,生產與生活中的折線圖、柱形圖、扇形圖、雷達圖在高考中都考查過.本題以社區環境建設中的“垃圾分類”為背景考查學生的數據分析能力,對數據處理與數學運算素養也作了相應的考查.
1.1.2 扇形弧長——浸潤數學文化
如第8題取材于我國古代科學家沈括的杰作《夢溪筆談》,以沈括研究的圓弧長計算方法“會圓術”為背景,以中華優秀傳統文化為情境材料設置試題,讓學生直觀感受我國古代科學家探究問題和解決問題的過程,讓學生領略中華民族的智慧和數學研究成果,進一步樹立民族自信心和自豪感,培育愛國主義情感.
1.1.3 概率統計——體現應用價值
如第19題以校園體育比賽為背景考查隨機事件的概率計算、隨機變量的概率分布列和期望.考查學生在現實情境下解決實際問題的能力,在試題的設計引導中加強體育鍛煉、勞動教育的理念.統計概率解答題注重知識的綜合應用與實際應用,作為考查實踐能力的重要載體,命題者要求考生會收集、整理、分析數據,能從大量數據中抽取對研究問題有用的信息,并作出判斷,進而做到由樣本數據估計總體特征.
1.2 重視基礎知識,考查關鍵能力
1.2.1 立體幾何——回歸基礎模型
如第18題,從題干來看,為常見的四棱錐模型,且底面特殊,對初中平面幾何的考查是本題的關鍵.設問為證明兩條直線垂直和求線面角的正弦值,主要考查基礎知識、基本方法,難度不大,屬于得分題.利用空間向量求空間角,運算錯誤是失分主要原因.
1.2.2 壓軸小題——狠抓關鍵方法
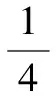
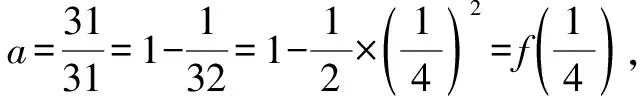
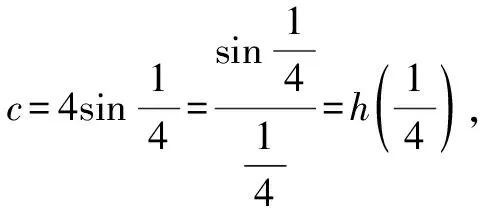
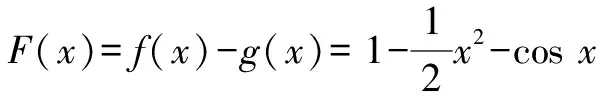
以往比較大小的問題,常表現為某函數當自變量取不同值時,比較函數值的大小.例如2021年新高考全國Ⅱ卷第7題:
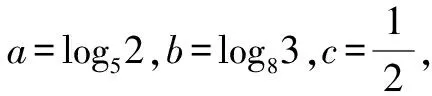
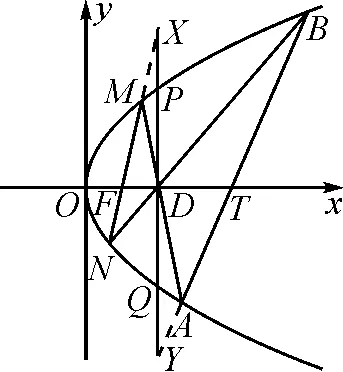
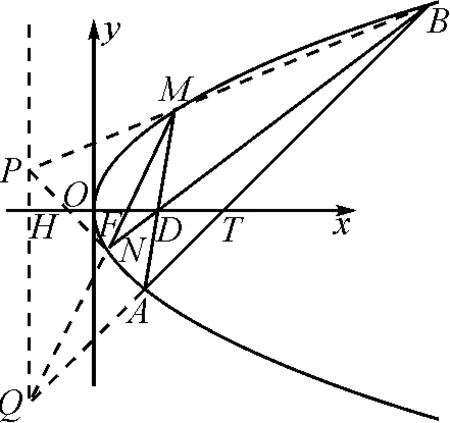
A.c C.a 高考不斷推陳出新,在這類問題中增加了放縮的成分,所比較的數據結構不完全一致,但可以通過放縮達到一致.例如2020年全國高考Ⅰ卷第12題: 若2a+log2a=4b+2log4b,則( ). A.a>2bB.a<2b 煙支重量是衡量香煙質量的一個重要指標[1],隨著人們對香煙質量要求不斷提高,煙支重量控制就顯得越來越重要;同時嚴格控制香煙平均重量,并保證煙支的重量標準差,能夠有效地控制煙草用量,有利于煙廠生產管理,降低成本,因此煙支重量控制引起了各煙草企業的高度重視[2]。 C.a>b2D.a 本題中,2a+log2a=22b+log2b=22b+log2(2b)-1<22b+log2(2b),結合函數y=2x+log2x在(0,+∞)上是增函數,可知a<2b.該題仍然沒有走出上述表現形式. 直到2021年全國乙卷理科第12題,其比較大小的理念發生了變化,添加了新的思想,即不同函數當自變量取同一值時的函數值的大小關系,這樣構造函數的難度有所提升,并且函數單調性的判斷難度也顯著升高.例如2021年全國乙卷理科第12題: A.a C.b 本題中,a,b大小關系的判斷仍可根據a=2ln 1.01=ln (1.012),利用y=lnx的單調性,轉化為比較1.012與1.02的大小關系,就可以判斷a與b的大小關系.但c與對數函數沒有關系,不得不采用以下策略: 2022年全國甲卷的第12題,明顯繼承了2021年全國乙卷的第12題的上述思想,事實上,2022新高考Ⅰ卷第7題亦如此.比較大小作為高考熱門題型,幾乎每年都會命制.甚至同一年中好幾套卷子都會命制,看似屢見不鮮的比較大小,實際上其中蘊含的方法和思想已經發生了變化,體現了高考題穩中見變,務實創新的命題風格. 1.2.3 關鍵位置——落實計算基礎 1.3.1 函數導數——突出轉化思想 1.3.2 解析幾何——檢驗綜合能力 如第20題(2)問,設拋物線C:y2=2px(p>0)的焦點為F,點D(p,0),過F的直線交C于M,N兩點.當直線MD垂直于x軸時,|MF|=3.設直線MD,ND與C的另一個交點分別為A,B,記直線MN,AB的傾斜角分別為α,β.當α-β取得最大值時,求直線AB的方程. 具體而言,由F,D均為定點,以及拋物線的性質可知直線AB與x軸的交點T也為定點,從而本題綜合了定值、定點問題;如圖1,直線XY垂直x軸于點D,交直線MN于點X,交直線AB于點Y,交拋物線于P,Q兩點.由蝴蝶定理知XD=YD,可據此簡化運算.如圖2,直線MN與AB交于點Q,直線PQ是點D的極線,從而本題綜合了配極變換;由D為定點得PQ為定直線,從而本題綜合了米勒問題. 圖1 圖2 全國甲卷連續三年以直線和拋物線為載體考查解析幾何的基礎知識以及基本思想方法,且分別以阿基米德三角形、彭賽列閉合定理、蝴蝶定理和米勒問題為問題背景,不僅豐富了高考試題的文化背景,也體現了穩中見變,務實創新的命題風格. 總之,2022年高考數學甲卷(理科)試題穩步過渡新、舊高考,繼續推進題型和試卷結構的改革,注重對基礎知識、基本能力的考查,對數學抽象、直觀想象、邏輯推理等核心素養都有較高的要求. 高考試卷中大量的試題考查四基,因此,儲備基礎知識,掌握基本方法,熟練基本題型,仍是備考工作永恒不變的首要任務.從本次考卷中呈現出的全集與補集、扇形弧長公式、分式函數值域問題等,都是高中階段最基本的數學知識,但是以往的考卷中并不多見,導致教學中對此不夠重視.因此備考時,特別需要注意對基礎知識查漏補缺. 近年來的高考試卷,都表現出比較大小、極值點偏移、函數同構是高考的熱點,它們雖然年年都考,但由于其綜合性強,學生掌握起來還是很有挑戰性.通過強化訓練可以克服這種困難,做到有備無患,這對于考場發揮和考試信心都有積極的作用. 試卷中第12題比較大小,第20題解析幾何問題,第21題導數問題作為試卷中的關鍵題目,它們呈現的共同規律就是轉化化歸、數形結合、函數與方程的思想和方法.數學作為解決問題的工具學科,其基本做法就是對問題進行轉化,把復雜問題簡單化,陌生問題熟悉化,而各種各樣的數學概念、公式、定理就是實現轉化的工具.因此,有必要提升學生轉化化歸的思想和能力,并且掌握常見的轉化技巧. 高考試卷雖然年年保持穩定性,但是總有局部創新的地方.本試卷中第12題比較大小就一反往日套路,其比較大小的思路與模式可謂“出乎意料之外,又在情理之中”.比較大小這類題小巧靈活,其創新的突破口更為多樣.又比如第20題解析幾何問題,把蝴蝶定理和米勒問題融入之中,這也是以往的試題所未見到的.因此,有必要精研考題,尋找考法的變化點與創新點,把握考向動態,融入更多元的考試素材,命制更具有選拔功能的模擬試題,這對于培養并發掘創新型人才大有裨益. 高考試卷的關鍵題目往往集中為幾個比較綜合的問題.比如該卷中第20題解析幾何問題,除通性通法外,又可以用蝴蝶定理、米勒問題的視角欣賞此題,此題雖然題面表現為最值問題,實際上其中蘊含著不少的定值、定點、定直線,深入研究不難發現其綜合性很強.又如第21題導數問題,除了通性通法外,又可以從極值點偏移、函數同構等視角欣賞并解答,綜合性可見一斑.因此,培養學生的綜合能力,提高學生的核心素養,是提升學生關鍵競爭力所必需的.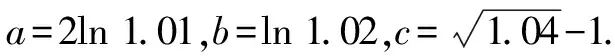
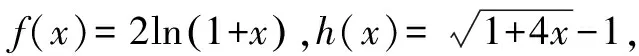

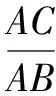

1.3 突出理性思維,考查學科素養
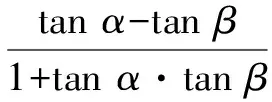
2 反思教學,指導備考
2.1 查漏補缺,夯實基礎
2.2 關注熱點,強化訓練
2.3 思想引領,理論提升
2.4 推陳出新,開拓進取
2.5 素養導向,綜合培育

