圓錐曲線最值問題的不同思路分析
?重慶市秀山高級中學校 胡 紅
1 定義法求最值
所謂定義法,主要是從幾何圖形的定義和性質著手找到其中的關系進而求最值的解題方法.運用定義法求解圓錐曲線最值問題,解題思路大致為:①找到與所求值相關的平面幾何定義或性質,如三角形兩邊之和大于第三邊等;②列出相關的不等式并求解,綜合考慮即可得到所求最值.如以下例1所示.
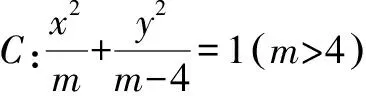
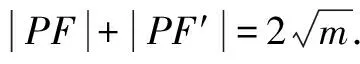
解:由題意可得,橢圓C的右焦點為F(2,0),則左焦點為F′(-2,0).
由|PA|+|PF|=8,可得
結合||PA|-|PF′||≤|AF′|=2,可得
解得9≤m≤25.
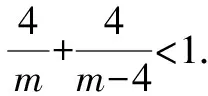
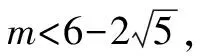
故m的最大值為25.
2 函數法求最值
運用函數法求與圓錐曲線有關的最值問題,主要是圍繞所求變量構造函數進而求出相關最值.用該方法解答圓錐曲線最值問題的大致思路為:①假設與所求問題相關的點的坐標為(x,y),建立所求量與假設變量的關系;②借助圓錐曲線方程和點到直線的距離公式,使問題轉化為以唯一變量表達的函數解析式;③判斷變量范圍進一步確定最值[1].具體解題步驟如例2所示.
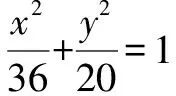
分析:本題包含許多未知點,需要按部就班求出相關點.首先設點P的坐標,根據題意列出與之相關的方程組,得到具體坐標;然后根據點M到直線AP的距離等于|MB|,得到|MB|的值與點M的坐標.由于問題是求橢圓上的點到點M距離的最小值,假設橢圓上任意一點為(x0,y0),根據兩點間距離公式得到函數解析式,進而求出所求距離的最小值.
解:設P(x1,y1)(y1>0).
由A(-6,0),B(6,0),F(4,0),可得
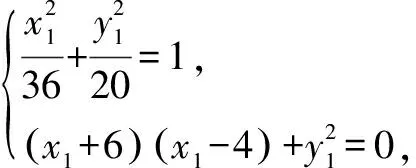
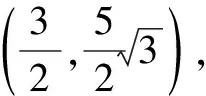
設M(m,0)到直線AP的距離為d,則
解得m=2,則點M(2,0).
設橢圓上任意一點N(x0,y0)到點M距離為d′,則
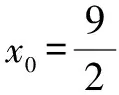
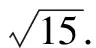
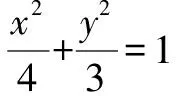
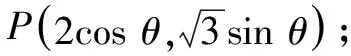
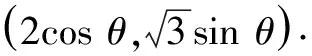
由題意可得F(-1,0),于是有
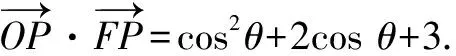
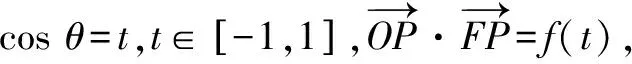
f(t)=t2+2t+3,t∈[-1,1].
因為函數f(t)的對稱軸為t=-1,所以函數f(t)在[-1,1]上單調遞增.
因此f(t)的最大值為f(1)=6.
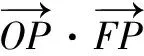
3 不等式法求最值
不等式法也是求解圓錐曲線最值問題常見的一種方法,主要借助基本不等式或柯西不等式求出相關最值[2].解題的大致思路為:①設出問題所涉及的元素的坐標或方程;②聯立圓錐曲線方程化簡得到只含有一個變量的方程,利用韋達定理求出x1+x2,x1x2的表達式,③將所求問題表達為與x1+x2,x1x2有關的式子,運用基本不等式或柯西不等式求出最值.具體解題思路和步驟如例3所示.
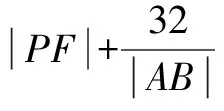
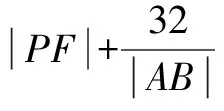
解:由題意得F(0,1).
設直線l:y=kx+1,A(x1,y1),B(x2,y2).
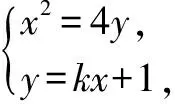
由韋達定理,得x1+x2=4k,x1x2=-4.
于是y1+y2=k(x1+x2)+2=4k2+2,
|AB|=y1+y2+2=4k2+4.
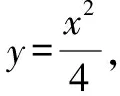
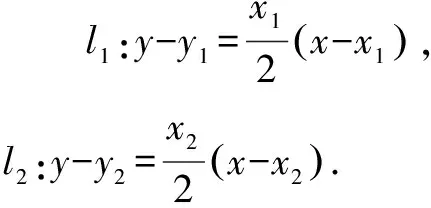
聯立l1,l2得到方程組并求解,得
所以點P(2k,-1),于是
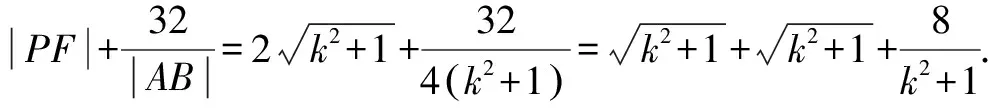
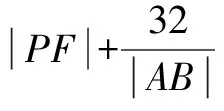
總之,根據上述不同的圓錐曲線求最值問題的例題分析,可以得到定義法、函數法以及不等式法的具體解題思路.針對不同類型的問題,采取相對應的方法進行解答.在解題過程中,應加強對已知條件的分析和應用,借助已知條件和相關性質構建不等式或函數.

