正態分布曲線在軸類零件生產線FTT的應用
肖 芝 凌 旭 戴俊良
(湖南化工職業技術學院機電工程學院,湖南 株洲 412000)
0 引言
首次合格率(First-Time-Through,FTT)是目前國際上監控生產線產品質量的一項重要的精益生產指標,是指一次性完成一個生產過程滿足質量要求的零件的百分率。例如,某一機加線包括工序1車、工序 2 銑、工序 3 鉆、工序 4 磨這四道工序,那么該線體的總體首次合格率為每道工序的首次合格率的乘積,可表示為FTT總=FTT1×FTT2×FTT3×FTT4,要注意的是,返工返修后的合格品不計入合格數。提升生產線的FFT 能有效降低生產過程的質量成本。正態分布即正常狀態下的隨機變量分布,影響隨機變量取值的各個因素都不起主要作用,且各個因素相互獨立,則該隨機變量服從的是正態分布。例如,人的身高體重、某班級期末考試成績、田里水稻的產量等。在機械制造業中,正態分布的應用也比較廣泛,特別是在質量管理方面,如零件加工尺寸分析、檢驗員的測量誤差分析、測量系統的誤差分析等。通過正態分布曲線不僅能預算批量生產加工零件的FTT、判定加工設備的工序能力,還可分析機械制造過程中加工誤差的性質,從而提升加工質量。
1 FTT的計算與分析
某渦輪增壓器轉子軸的機械加工生產線共有10 道工序,即工序1(鉆中心孔)、工序2(雙刀架粗車加工)、工序3(小徑磨削加工)、工序4(密封槽的磨削加工)、工序5(大徑磨削加工)、工序6(渦輪輪廓磨削)、工序7(去毛刺)、工序8(動平衡)、工序9(激光打標)、工序10(檢驗入庫)。其中,工序3、工序6為關鍵工位。
對現場收集到的當日報表數據進行統計,當天共投入毛坯215 件,產出合格件214 件,合格率為99.53%。在各工序中,工序1、工序2、工序4、工序6、工序 7、工序 9、工序10 的 FTT 均為 100%,工序 3 返工10件,工序5返工1件,工序8報廢1件。根據FTT的計算方法,則FFT=100%×100%×95.35%×100%×99.53% ×100%×10總0%×99.53%×100%=94.45%。合格率與首次合格率間的差異在于返工數,大量的返工零件不僅增加整個流水線的時間節拍、降低生產效率,還在一定程度上擾亂整個生產節奏,使生產管理的難度進一步提高。從上述分析可以看出,工序3(小徑磨削加工)是制約FTT 提升的關鍵工序。
2 數據收集及正態分布曲線分析
2.1 數據收集
工序3 為軸徑尺寸的磨削精加工,其尺寸要求為?4.11+00.005,精度等級高,直接影響產品的性能及可靠性。因此,對該工位的尺寸質量進行嚴格管控,通過通止規進行百檢。為了提升工序3 的FTT指標,從庫房中隨機選取首次合格的50件203零件進行尺寸測量,并隨機從工序3返工的10件零件中抽取2 件返工前測量記錄的尺寸數據,共52 組數據,見表1。

表1 工序3軸徑尺寸測量值
2.2 正態分布曲線
正態分布的函數形式見式(1)。
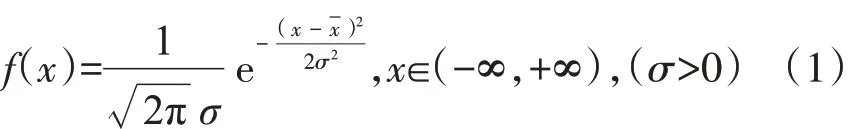
式中:σ 為樣本標準差;x 為樣本均值;x 為隨機變量;f(x)為發生xn隨機變量的概率。
其中,樣本均值x 和樣本標準差σ 的計算公式見式(2)、式(3)。

由正態分布函數的表達式可知,正態分布曲線是由平均值x 與標準差σ 來決定的,令f(x)=y,以y為縱坐標,x為橫坐標,正態分布曲線見圖1。
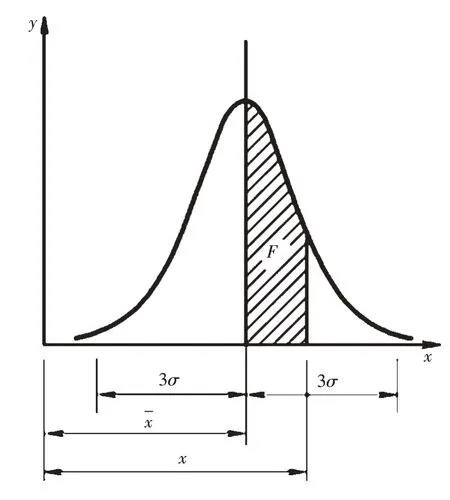
圖1 正態分布曲線圖
正態分布曲線與x軸所包含的圖形面積為全部隨機變量出現的概率,其總面積為100%,見式(4)。
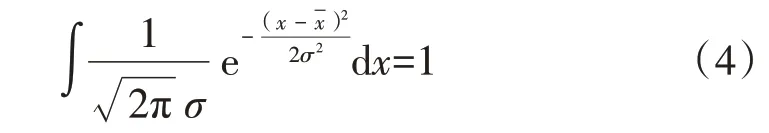
在圖1 中,F 區域的面積表示某隨機變量x 測量值到總樣本平均值x 之間數值區域出現的概率值,計算公式見式(5)。

計算出Z 值,通過標準正態分布概率表即可得出F值。
2.3 正態性檢驗
在對數據進行正態分析前,要檢驗收集到的數據的正態性。本研究使用質量統計分析軟件Minitab 對表1 中數據的正態性進行檢驗。將52 組測量值作為被檢驗的隨機變量,檢驗方法選擇Ryan-Joiner。檢驗結果P值>0.05,可認定該數據服從正態分布。其中,數據樣品的均值x=4.114 17、標準差σ=0.000 785 2,如圖2 所示。如果出現數據類型不服從正態分布的,可檢查數據樣本量是否過少或數據中存在隨機誤差[1]。
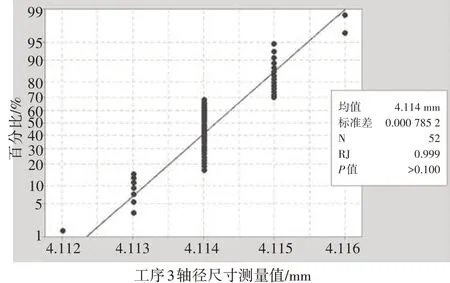
圖2 正態性檢驗
2.4 工序能力判定
工序能力指數是判明工序的實際加工精度能否滿足公差要求的程度指標,用Cp來表示。Cp=控磨床的工序能力。工序3 中所加工零件的尺寸公差為0.005 mm,根據2.3 中所得標準差σ=0.000 785 2,可得工序3 的工序能力指數Cp=1.061。根據表2可判定工序3臥式數控磨床設備的工序能力一般,屬二級工藝,基本能滿足軸徑磨削的加工精度[2]。

表2 工序能力等級
2.5 整體樣本合格率預測
根據正態分布的特征,限值為4.110~4.115 mm(工序3 加工軸徑的尺寸下上偏差值)的正態分布曲線與x 軸所圍成的區域面積即為整體樣本的合格率[3]。可將整體樣本合格率以平均值x為界分為左右兩部分區域,分別計算二者的面積,如圖3所示。
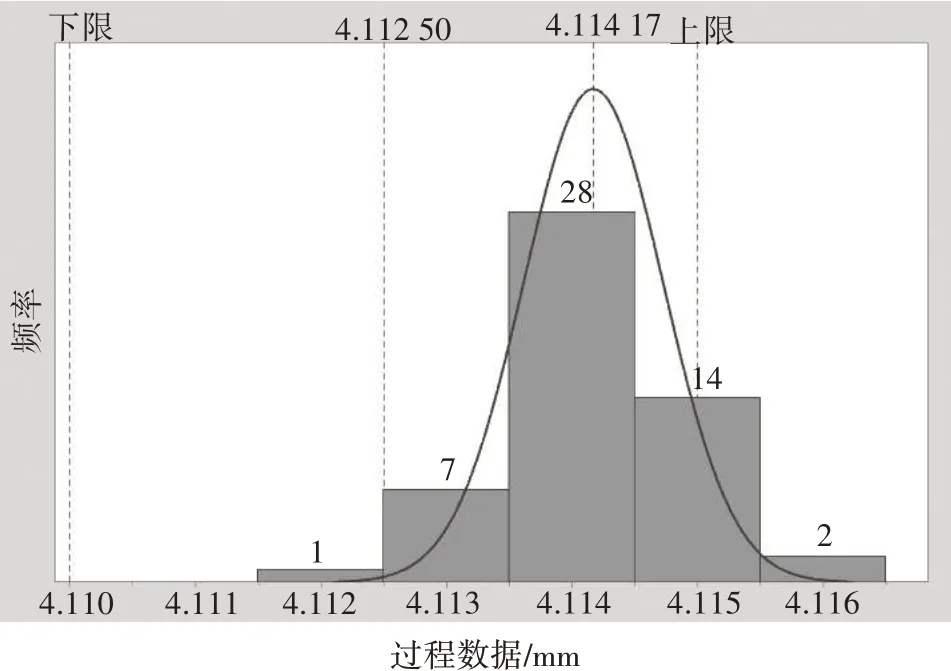
圖3 工序3測量數據正態分布曲線
4.114 17~4.115 mm(上偏差至x)的區域面積可通過公式(6)計算得到,即Z=(4.115-4.11417)/σ=1.057,查詢標準正態分布概率表可得右邊區域面積=0.7109/2=0.355 45,合格率即為35.55%。同理可計算出左邊區域面積為0.5,合格率即為50%,整體樣本的合格率等于左右兩部分區域面積之和,即整體樣本合格率為85.55%,即為整體樣本FTT 預測值,這與2.1 中的FTT 計算值95.35%有差異,這跟FTT 樣本數據量的大小有關,只要FTT 的樣本量足夠大,其值一定趨于95.35%。
2.6 問題排查及改進措施
從圖2正態分布曲線圖可以看出,實際尺寸測量平均值x=4.114 17 mm,與理論平均值4.112 5 mm相差0.00167 mm,實際分布曲線向左偏移了0.00167 mm。如果正態分布曲線未發生偏移,FTT 計算值為99.72%。因此,導致FTT數據指標下降的直接原因為平均值數據發生了偏移。
出現偏移的主要原因有2 個。一是加工過程中砂輪的徑向進給量過于保守,二是砂輪的修正頻次(每10件修正1次)過低。由于企業生產任務緊,考慮生產效率,暫不對砂輪的頻次改進修正。因此,提升FTT 的改進措施為適當增加磨削徑向進給量[4]。
3 問題跟蹤及驗證
根據2.5 中正態分布曲線偏移量0.001 67 mm,將改進措施中的參數設定為在原有磨削徑向進給量增加0.001 5 mm,并試驗跟線一天,統計FTT值。
3.1 數據統計
據現場統計的數據,當天共投入試驗毛坯218件,產出合格件216 件,合格率為99.08%,FTT=98.63%123總。在各工序中,工序 、工序 、工序 、工序4、工序6、工序7、工序9、工序10的FTT均為100%,工序 5 返工 1 件,工序 8 報廢 2 件。可得出工序 3 的FTT=100%,跟實施改進措施前有較大的提升,達到預期效果。為得到進一步數據進行理論驗證,隨機抽檢52件零件,并對工序3加工的軸徑尺寸進行測量,測量數據見表3。

表3 改進后工序3軸徑尺寸測量值
3.2 正態性檢驗
根據2.3 中的步驟,可得出正態性檢驗結果,P 值>0.05,可認定該數據服從正態分布,其中數據樣品的均值x=4.113 25,標準差σ=0.000 789 0,如圖4所示。
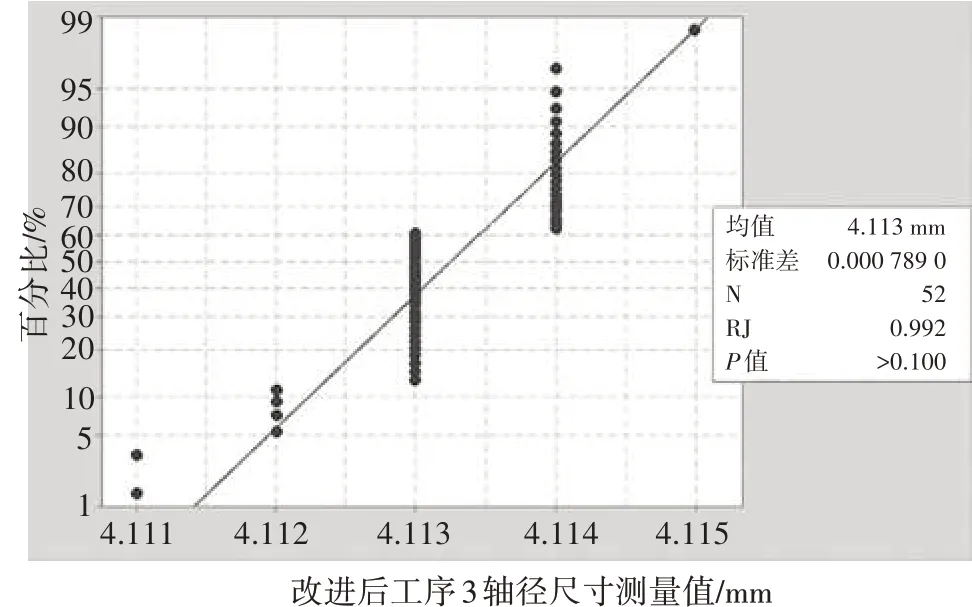
圖4 改進后尺寸數據的正態性檢驗
3.3 改進后整體樣本合格率預測
圖5 為改進后測量數據的正態分布曲線,其均值相對理論正態分布曲線中心4.112 5 mm,向左偏移0.000 75 mm。根據2.4 中的計算過程,整體樣本合格率為98.65%,即FTT=98.65%,相比改進前提升了近13個百分點,取得良好效果[5]。
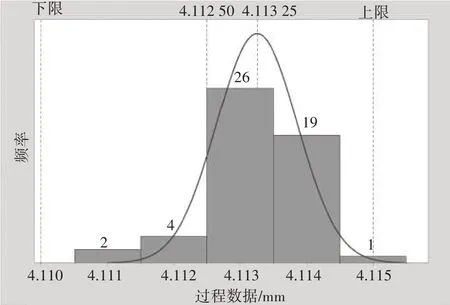
圖5 改進后測量數據正態分布曲線
4 結語
本研究通過對正態分布曲線進行分析,可有效提升某渦輪增壓器轉子軸機械加工生產線的FTT值,可大幅度降低大批量生產線的質量成本。為正態分布曲線在解決實際生產過程中的產品質量問題提供理論與實踐依據。質量管理要以實際生產數據為依據,運用數理統計等相關理論知識對生產過程中各個要素進行分析,從而不斷提升產品質量。對工序3 的工序能力Cp值,可根據企業實際情況進行提升,由于影響產品質量的因素復雜,一旦某個因素發生變異,出現不合格品的風險將增加。適當提高砂輪的修正頻次是不錯的提升措施。

