運用題組式教學優化學生知識結構的策略研究

☉高曉發

所謂的題組式教學是由一些題型結構相同、解題方法存在聯系的若干道題目共同組成的。在數學課堂上運用題組式教學，不僅可以讓學生“練一組題”“通一類題”，提高他們解同類題的能力，而且還有利于讓學生以數學的思維來觀察世界，促進其數學素養的形成和穩步提升。［1］因此，教師要做的就是從復雜的習題中精心挑選題目，盡可能地選三到五個題目來構成一組，引導學生在題組式練習中形成科學的思維，構建完善的數學知識結構，最終獲得綜合性的發展。

一、題組式教學的功能與作用

（一）激發學生的能動性

學生是一切學習活動的“主體”，自主探究是新課程標準所倡導的一種學習方式，要想進一步優化學生的知識結構，就要充分發揮題組式教學的作用，想辦法提高學生自主分析、獨立解題的興趣。題組式教學是對傳統單一習題的優化設計，避免了讓學生進行機械、重復性的練習，在一定程度上減輕了他們做練習的負擔，同時還能強化練習的效果。此外，題組式教學還克服了以往“一題一練”的弊端，能夠讓學生的數學練習變得更多彩、更輕松，從而激發他們的能動性。

（二）促進知識的系統性

做許多練習的目的就是為了讓學生能夠把在課堂上學到的比較零碎的知識“串聯”起來，讓頭腦中過于分散的知識變得更集中、更系統。而題組式教學是經過教師系統規劃的，其中的多道練習題也是由教師精心挑選的，在設置題型的時候，教師必須全面考慮知識間是否具備聯系，盡可能地捕捉到新、舊知識間的“銜接點”，在知識間搭建一個穩固的“橋梁”，從而讓學生在練習的過程中掌握知識間的縱橫聯系。而且，題組式教學具有層次性、系統性，可以對瑣碎、零散的知識進行串聯，起到“化零為整”的作用，有助于學生系統知識網絡的構建。

（三）提高思維的邏輯性

題組式教學有著結構性強、思維含量高的特點，通過大量的題組練習有利于學生的思維獲得由淺至深的發展，促使學生通過自己的思維來分析、建構題組練習，在處理這些題組的過程中，學生需要搞清楚它們之間的邏輯聯系，并分析習題之間的規律，他們思考問題時也會更加有序、更加嚴謹。所以說，開展題組式教學對于訓練學生思維的邏輯性有著較大的作用。

二、運用題組式教學的基本原則

（一）典型性原則

在構建題組時不能隨意、盲目，應精心挑選具有典型性的數學題目，盡可能地選擇那些與教學內容互相貼合的練習題來組成題組，使學生在典型的練習題中習得要點知識、挖掘知識間的聯系，從而深化他們對知識的掌握。［2］因此，在運用題組式教學時教師要遵循“典型性”的基本原則，力求讓學生達到“會一題會一類題”的最佳效果。

（二）循序漸進原則

在具體的教學中，教師必須充分考慮小學階段學生思維發展的具體規律，根據他們的思維水平來實施題組式教學，題組應該從易到難地給學生呈現，這樣才能符合他們的認知規律，讓學生的思維從淺層向深層逐步發展。與此同時，這樣還有利于顧及數基金項目：甘肅省教育科學“十四五”規劃2021 年度一般課題《運用題組式教學幫助小學生構建數學知識脈絡的策略研究》（GS［2021］GHB0271）的研究成果之一。學基礎不同、接受能力存在差異的學生，保證題組練習面向所有學生，從而促進班里學生的共同發展。［3］

（三）多樣性原則

多樣性的原則是指，教師必須擺脫以往單一、枯燥的練習模式，根據復習課的類型以及學生的實際情況來調整題組式教學，在具體的教學中，題組的類型也不是固定不變的，可以圍繞知識點的難易程度來設計多種類型的題組，這樣才能適應學生的多元需求，通過多樣化的題組練習來鍛煉學生的思維力。因此，教師要遵循“多樣性”的原則來實施題組式教學。

三、運用題組式教學優化學生知識結構的策略

（一）編擬“題組”的策略

1.在知識易混處，設計“對比性”題組

烏申斯基提出，比較是讓學生深入理解某件事物的重要方式，人們也是通過一系列的比較活動來了解周圍世界的。［4］因此，教師可以針對學生容易混淆的知識來開展題組式教學，圍繞學生的實際水平設計“對比性”題組，讓學生對題組中所呈現的不同題目展開對比、分析，進一步把握題目之間的區別，從而達到深化記憶、強化知識掌握的目的。

例如，在組織學生學習北師大版二年級《倍的認識》這部分內容時，教師就圍繞學生的發展水平設計了一組具有系統性的練習題：

（1）紅色花的數量是黃色花的（ ）倍；（黃花2 朵，紅花6 朵）

（2）紅色花的數量是黃色花的（ ）倍；（黃花2 朵，紅花8 朵）

（3）紅色花的數量是黃色花的（ ）倍。（黃花3 朵，紅花6 朵）

學生在分析的過程中逐步列出相應的式子：（1）2×3 ＝6；（2）2×4 ＝8；（3）3×2 ＝6。然后對這三個式子對比、觀察，從中得出3 倍、4 倍、2 倍的結果。因為二年級的學生對于“倍”這個概念認識不夠深，所以在教學中教師運用到生活中“比較花朵數量”的例子，讓學生在列式、分析的過程中感知到倍數的存在。通過這組練習題，學生能夠初步理解“倍”的概念，即使今后教師再給學生出示類似的習題，他們也可以分辨出另一份是這一份的幾倍。

2.在知識關鍵處，設計“針對性”題組

針對某個關鍵的知識點，教師可以設計相應的題組練習，幫助學生在練習的過程中逐步內化這個關鍵點，掌握知識的本質。在具體的教學中，如果教師還是采取傳統孤立解答一道題的練習方式，就算學生解決得再好，也不過是完成了對單個問題的解決，不利于促進他們邏輯思維的形成。所以教師可以精心挑選一些類似的、有聯系的題目，設計“針對性”的題組，變成“一題多用”，讓學生的思路逐步拓寬，使他們在解決多個問題的過程中掌握更靈活的數學思維。

例如，為了讓學生掌握“歸納”這個重要的思想，教師向學生出示了四個算式：

（1）1 ＋3 ＝

（2）1 ＋3 ＋5 ＝

（3）1 ＋3 ＋5 ＋7 ＝

（4）1 ＋3 ＋5 ＋7 ＋9 ＝

……

這個題組剛好包含了歸納的方法，需要學生進一步觀察這幾個算式間的聯系，尋找共同點，通過分析就能看出“這幾個相加的數字都是奇數”“計算出來的和都是平方數，如4、9、16 等”，接著學生繼續往后展開計算，并嘗試總結這一題組的本質特點，最后得出“從1 開始，連續奇數的和都是平方數”這一結論。通過針對性題組的練習，可以讓學生實現思維水平的提升，并掌握數學學習的重要思想——歸納。

3.科學“變”題，設計“變式性”題組

題組式教學不能光停留在表層，教師要對現行教材的內容進行認真研讀，在此基礎上根據本班學生的學情來設計“變式性”題組，科學“變”題，以此來開拓學生的思維。可見，通過對“變式性”題組的練習有利于讓學生在形成知識結構的過程中進行思維發散，從而提高他們思維的廣度與深度，讓學生在題組練習中獲得綜合性的發展。

例如，在組織學習“加與減”的過程中，教師設計了以下題組：

（1）三年二班的男生19 人，女生比男生要多8 人，請問女生有多少呢？

（2）有一輛小汽車每個小時可以行進50 公里，而火車每個小時比它快40 公里，請問火車的速度是多少？

（3）在一個停車場一共有42輛自行車，而自行車的數量要比轎車少12 輛，請問一共有多少轎車？

第一道練習題是讓學生用“正推”的方式來求大數，到了第二道題就換成了“速度”的形式，但本質上也是計算大數，第三個練習題則是考驗學生的“逆推”能力，需要學生改變自己的思維。在這個題組練習中，可以讓學生明白，不是看到誰比誰“多”就要用加法，同樣的，不是看到誰比誰“少”就要用減法，必須要認真讀題來分析大數、小數之間的關系。在解決題組的過程中可以讓學生發現這三道題目形式雖然靈活、多樣，但是結構還是一樣的。通過這樣的方式可以更好地訓練學生的思維。

（二）典型案例的分析

筆者在講授《有余數的除法》一課時，嘗試了科學運用題組式教學來優化學生的知識結構。

首先，通過游戲的形式來引入本課。

1.請同學們思考在括號內最大可以填數字幾。

（ ）×5＜31

（ ）×4＜22

（ ）×3＜20

6×（ ）＜34

5×（ ）＜38

7×（ ）＜24

導入環節的題組練習主要是為了考查學生對于乘法口訣的掌握情況，讓學生體驗“最大試商”的具體過程，一方面是為了激活學生已學知識，另一方面是為了接下來有余數的除法學習做好鋪墊，通過題組的形式來打開學生的思維。

其次，共同探究有余數的除法。

2.張三今天帶來14 根香蕉，想把它們分給班里的好伙伴，請你們來幫幫他，想一想可以怎么分？例如分給幾個小伙伴，每個人可以分到幾根香蕉，是否還會有剩余的香蕉？

最后，把分香蕉的情況以表格的形式呈現出來，見表1。

3.你們是否可以把表1 中的這些分法來分分類呢？

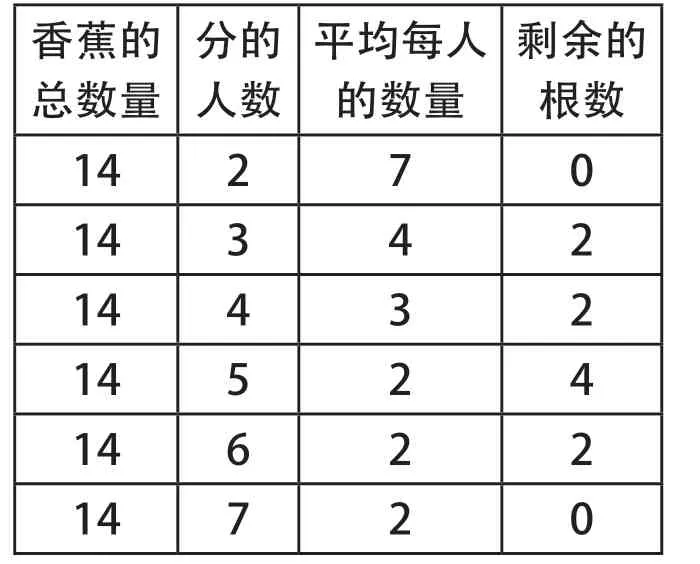
表1 香蕉分配情況表

讓學生分成兩類，有余數的是一類，沒有余數的是一類，并列出相應的算式。例如沒有剩余的算式是：（1）14÷2 ＝7；（2）14÷7 ＝2。有剩余數量的算式是：（1）14÷3 ＝4……2；（2）14÷4 ＝3……2；（3）14÷5＝2……4；（4）14÷6 ＝2……2。這時，教師引導學生對余數和除數進行細致觀察，說一說從中可以發現什么。例如，有的學生對二者的大小關系進行了對比，發現“余數小、除數大”的共同點。在整個過程中，教師給學生提供了充分的思維空間，讓他們根據題組形式的算式來分析除數、余數的關系，從而得出相應的結論。

4.接下來我們檢驗下列式子哪些是正確的。

（1）判斷題

①16÷3 ＝4……4（ ）

②24÷5 ＝4……4（ ）

③18÷3 ＝5……3（ ）

（2）選擇題

①15÷6 ＝2……？，它的余數是多少？

A.6 B.3 C.7

②32÷9 ＝3……？，它的余數是多少？

A.5 B.8 C.2

③下面幾個算式正確的是：

A.14÷7 ＝1……7

B.19÷8 ＝2……2

C.27÷4 ＝6……3

D.17÷8 ＝1……9

教師在課堂練習環節中也使用了題組式教學，第一道判斷題主要是讓學生利用“余數比除數小”的原則來進行判斷；第二道選擇題主要是讓學生通過計算來得出最終的答案。與第一題相比，第二題具有一定的坡度，學生需要進行多道有余數除法的練習，從而綜合運用本節課所學到的知識。像這樣具有層次的題組練習設計可以讓學生的思維獲得由淺至深的發展，幫助學生更牢固地掌握本節課的知識，促進其知識結構的優化。

綜上所述，題組式教學在一定程度上可以解決傳統數學教育“遍布題海”的弊端，為提高練習的效率提供有效的途徑，所以教師要加強對題組式教學的利用，充分結合小學階段學生身心發展規律以及思維特點來設計多種類型的題組，讓學生對精選的習題進行分析和解決，在此過程中形成比較靈活的思維，掌握解決類似數學問題的方法，讓每一個題組都能達到應有的效果，最終幫助學生構建完整的數學知識網絡。