基于優勢關系的畢達哥拉斯模糊三支決策模型①
趙杰, 萬仁霞, 苗奪謙
1.北方民族大學 數學與信息科學學院,銀川 750021;2.同濟大學 電子與信息工程學院,上海 201804
三支決策(Three-Way Decision)是由文獻[1]提出的一種決策理論,該理論深刻地刻畫了決策者對不確定事物的決策行為. 在實際決策過程中,對具有充分把握做出判斷的事物采取接受或拒絕決策,對不能立即做出判斷的事物,采取延遲決策,即通過分治模型和序貫策略,采取三分而治和化繁為簡的方法來分析和解決復雜決策問題[2],由于三支決策符合人們的決策思維,它一經提出便受到國內外學者的廣泛關注. 文獻[3]將三支決策與形式概念分析結合,提出了三支形式概念分析,拓展了三支決策理論. 此外,文獻[4]將半概念與三支概念分析結合,提出了必然-可能半三支概念,拓展了三支概念分析理論. 文獻[5]將三支決策思想引入到概念簇中,提出了三支概念簇的概念,使其能夠檢索到更加符合需求的對象.
模糊集(Fuzzy Sets)是由文獻[6]提出的. 該理論將經典集合進行了擴充、 推廣[7],準確地闡述了模糊性的含義. 然而非隸屬度同樣發揮著重要作用,文獻[8]提出并定義了直覺模糊集的概念及其運算,從而能夠細膩地刻畫客觀世界的模糊性本質,進一步拓展了模糊集. 文獻[9]基于隸屬度與非隸屬度的平方和不超過1的假設,提出了畢達哥拉斯模糊集,畢達哥拉斯模糊集相較于直覺模糊集具有更強的表達模糊性的能力并且受到廣泛關注,文獻[10]在沖突分析中利用畢達哥拉斯模糊數來表達局中人對議題的態度,并進一步應用到群體決策中. 文獻[11]對具有多參數的畢達哥拉斯集,提出了新的相似性度量,并將其應用到模式識別.
本文在畢達哥拉斯模糊集的優勢關系下,建立了畢達哥拉斯模糊三支決策模型,相較于文獻[12],計算方法簡單,實用性強,并且不需要求解條件概率. 根據現實需要,構建了區間畢達哥拉斯模糊三支決策模型. 另外,根據決策者的風險偏好,討論了樂觀型畢達哥拉斯模糊三支決策和悲觀型畢達哥拉斯模糊三支決策.
1 預備知識
定義1[12]設U={x1,x2,…,xn}是一個有限非空集合,則U上的一個畢達哥拉斯模糊集為
P={〈x,uP(x),vP(x)〉:x∈U}
(1)
其中uP(x),vP(x)∈[0,1]表示U中的元素x屬于畢達哥拉斯模糊集P的隸屬度和非隸屬度,并且滿足
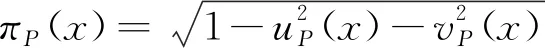
定義2[13-14]設U={x1,x2,…,xn}是一個有限非空集合,對于任意的X?U,X上的一個區間畢達哥拉斯模糊集A被定義為

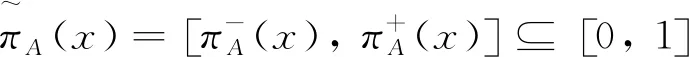

定義3[12]設p(x)=〈uP(x),vP(x)〉為畢達哥拉斯模糊數,其得分函數與精確函數分別為
假設p1(x)=〈uP1(x),vP1(x)〉,p2(x)=〈uP2(x),vP2(x)〉為兩個畢達哥拉斯模糊數,則:
(a) 如果Score(p1(x)) (b) 如果Score(p1(x))=Score(p2(x))且Accuracy(p1(x)) 定義4[15]假設四元組S=(U,A,VPF,f)為一個畢達哥拉斯模糊信息系統,對于?x1,x2∈U,?a∈A,x1,x2在屬性a下對應的畢達哥拉斯模糊數分別為 f(x1,a)=〈ua(x1),va(x1)〉 f(x2,a)=〈ua(x2),va(x2)〉 稱 R1={(x1,x2):f(x1,a)≤f(x2,a),?a∈A} 為畢達哥拉斯模糊信息系統的優勢關系,記[x]R1為包含元素x的優勢類,則S是一個具有優勢關系的畢達哥拉斯模糊信息系統. 定義5[15]設U是一個非空集合,R1為定義在非空集合U上的優勢關系,記apr=(R1,U)為優勢空間,對?X?U,其下近似和上近似被分別定義為 下近似和上近似將論域劃分為3個部分,即 定義6[1]設三元組(U,AT,f)為一個信息系統,其中U為所有對象的有限非空集合,AT是所有屬性的有限非空集合,f表示U與AT之間的關系. 狀態空間Θ={X,X}表示對象x是否屬于集合X.aP,aB,aN分別表示對象x確定屬于、 可能屬于、 確定不屬于X的行動,不同狀態下對應的3種不同行動的風險代價函數如表1所示. 表1 不同行動下的風險代價函數 當一個對象x屬于X時,采取aP,aB,aN所需的代價分為λPP,λBP,λNP. Pr(X|[x])表示對象x所在的等價類屬于集合X的條件概率,對于特定的對象x,采取一個決策行動的期望損失為R(ai|[x]) (i=P,B,N),如(2)式所示: R(aP|[x])=λPPPr(X|[x])+λPNPr(X|[x]) R(aB|[x])=λBPPr(X|[x])+λBNPr(X|[x]) (2) R(aN|[x])=λNPPr(X|[x])+λNNPr(X|[x]) 由Bayes風險決策理論,給出最小決策代價規則: (P) 如果R(aP|[x])≤R(aB|[x])且R(aP|[x])≤R(aN|[x])成立,那么x∈POS(X); (B) 如果R(aB|[x])≤R(aN|[x])且R(aB|[x])≤R(aP|[x])成立,那么x∈BND(X); (N) 如果R(aN|[x])≤R(aP|[x])且R(aN|[x])≤R(aB|[x])成立,那么x∈NEG(X). 另外還需考慮兩個因素: Pr(X|[x])+Pr(X|[x])=1;λPP≤λBP≤λNP,λNN≤λBN≤λPN. 因此得到簡化的最小決策代價規則: (PP) 如果Pr(X|[x])≥α且Pr(X|[x])≥γ成立,那么x∈POS(X); (PB) 如果Pr(X|[x])≤α且Pr(X|[x])≥β成立,那么x∈BND(X); (PN) 如果Pr(X|[x])≤β且Pr(X|[x])≤γ成立,那么x∈NEG(X). 其中 對于優勢空間,根據定義6,采取aP,aB和aN這3種決策行動的期望損失分別為 R(aP|[x]R1)=λPPPr(X|[x]R1)+λPNPr(X|[x]R1) R(aB|[x]R1)=λBPPr(X|[x]R1)+λBNPr(X|[x]R1) (3) R(aN|[x]R1)=λNPPr(X|[x]R1)+λNNPr(X|[x]R1) 在畢達哥拉斯模糊集中,隸屬度u與非隸屬度v之和等于1是不定的,因此本文參考文獻[16]的方法,設置糾偏參數ε(-1≤ε≤1),使得u2+v2+ε2=1,對于特定對象x的第i個畢達哥拉斯模糊數〈ui(x),vi(x)〉,采取接受、 延遲、 拒絕決策的期望損失分別如(4)式所示 Ri(aP|[x]R1)=λPPui(x)+λPNvi(x) Ri(aB|[x]R1)=λBPui(x)+λBNvi(x) (4) Ri(aN|[x]R1)=λNPui(x)+λNNvi(x) (PP′) 如果采取接受決策,則有 (5) 進一步整理(5)式后得 (PB′) 類似于(PP′),若采取延遲決策,則經化簡后可得 (PN′) 類似于(PP′),若采取拒絕決策,則經化簡后可得 為保證邊界域有解空間,令αi(x)>βi(x),從而有 因此 0≤βi(x)<γi(x)<αi(x)≤1 當ui(x)≥αi(x)時,采取接受決策;當βi(x) 決策規則1設S=(U,A,VPF,f)為畢達哥拉斯模糊信息系統,對于?X?U,?x∈X, (i) 當ui(x)≥αi(x)時,采取接受決策; (ii) 當βi(x) (iii) 當ui(x)≤βi(x)時,采取拒絕決策. 其中 當隸屬度與非隸屬度為區間值時,決策者采取aP,aB和aN這3種決策行動的期望損失分別為 定義7[17]對于任一區間[a,b],風險參數θ∈[0,1],有 fθ=(1-θ)a+θb (i) 對于規則(PP″), (6) (6)式化簡為 (ii) 類似于(i),對于規則(PB″),經化簡后得 (iii) 類似于(i),對于規則(PN″),經化簡后得 決策規則2在畢達哥拉斯模糊系統S=(U,A,VPF,f)中,對于任意的x∈U,有: 其中 由定義7知,當風險參數θ=0時,決策時要求隸屬度最小,將集合元素劃分到正域、 負域或邊界域的期望損失最小;當θ=1時,決策時要求隸屬度最大,將集合元素劃分到正域、 負域或邊界域的期望損失最大. 由此,進一步可以得到上述模型的兩類重要類型: 例1U1中含有8個數據對象,如表2所示. 表2 U1中的數據信息 不同狀態下對應的3種不同行動的代價損失函數取值分別為λPP=0.6,λPN=2.2,λBP=1.3,λBN=1.4,λNP=2.2,λNN=0.4. 在畢達哥拉斯模糊三支決策模型中,根據決策規則1,所得決策結果如表3所示. 表3 決策結果 例2U2中含有7個數據對象,如表4所示. 表4 U2中的數據信息 不同狀態下對應的3種不同行動的代價損失函數的取值分別為λPP=0.3,λPN=3.0,λBP=1.1,λBN=1.4,λNP=3.0,λNN=0.6. 樂觀型決策者 當風險參數θ=0時,根據樂觀型區間畢達哥拉斯模糊三支決策模型的決策規則,相應的決策結果如表5所示. 表5 θ=0時的決策結果 悲觀型決策者 當風險參數θ=1時,由悲觀型區間畢達哥拉斯模糊三支決策模型的決策規則,相應的決策結果如表6所示. 表6 θ=1時的決策結果 本文基于畢達哥拉斯模糊集的優勢關系,構建了集合優勢類,對論域進行了劃分. 根據Bayes最小風險決策理論,構建了畢達哥拉斯模糊三支決策模型,并對閾值進行了討論. 進一步構建了區間畢達哥拉斯模糊三支決策模型,討論了該模型的樂觀型和悲觀型兩類特殊情況. 本文是對三支決策理論的有益補充,細膩地刻畫了不同風險偏好下的決策問題. 畢達哥拉斯模糊集具有較強的處理不確定信息的能力,用畢達哥拉斯模糊數表示對象與屬性之間的關系具有重要意義. 然而在現實決策中,并不能確定對象與屬性關系的真假,換言之,在這種形式背景下會出現真、 假隸屬度,如何確定對象與屬性間的真實關系并進行決策將是我們未來所研究的內容.
2 基于優勢關系的畢達哥拉斯模糊三支決策模型

3 區間畢達哥拉斯模糊三支決策模型
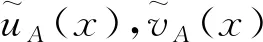
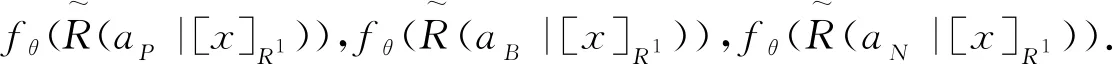
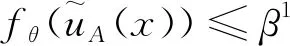

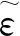
3.1 樂觀型區間畢達哥拉斯模糊三支決策
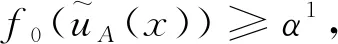
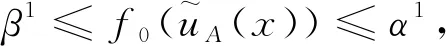
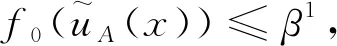
3.2 悲觀型區間畢達哥拉斯模糊三支決策


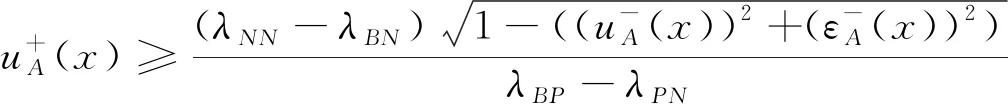
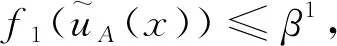
4 案例分析

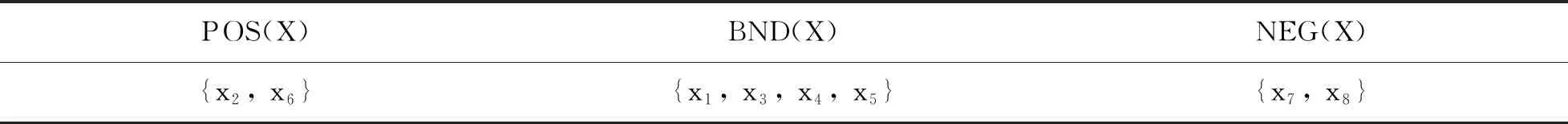

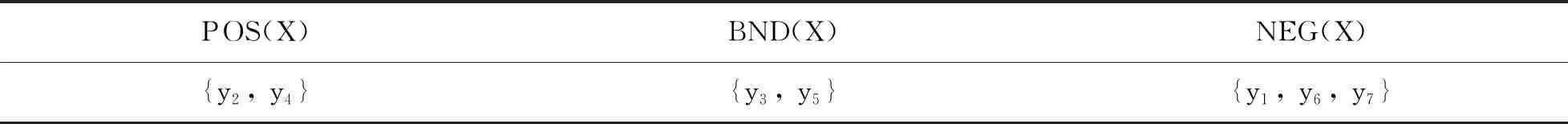
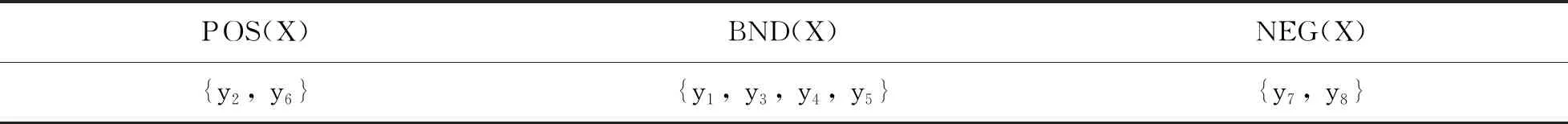
5 總結

