面向空間目標相對軌道確定的編隊優化方法

李佳興，袁 利,2，張 聰，張斯航，孫 棟

(1.北京控制工程研究所，北京 100094；2.空間智能控制技術重點實驗室，北京 100094)

0 引 言

以可見光相機為代表的被動式測量裝置廣泛應用于空間監視和空間碰撞預警等任務[1]。通過對空間目標非分辨點成像數據的處理，可獲得其相對航天器的視線測量信息，基于視線測量信息的空間目標相對軌道確定方法成為保證航天器在軌安全運行的重要手段[2]。

單視線測量信息缺少航天器與空間目標的相對距離信息，可觀測度差，造成相對軌道確定算法收斂慢甚至不收斂[3]；而利用多航天器對空間目標的視線信息可顯著提高系統可觀測度，進而提高空間目標軌道確定精度。文獻[4-5]利用兩個航天器的雙視線測量信息以及兩個航天器之間的距離信息，通過集中式濾波方法確定空間目標相對軌道，并且說明系統可觀測度與雙視線夾角相關。考慮到采用集中式濾波方法時系統狀態估計維數高，高學海等[6]采用分布式濾波方法完成空間目標相對軌道確定，龔柏春等[7]則考慮多個航天器場景，通過多個航天器間的位置約束，采用一致性擴展卡爾曼濾波方法，提高了空間目標相對軌道確定精度。以上研究都需要航天器間基線信息，Li等[8]考慮無法獲取基線信息的場景，僅利用兩個航天器對空間目標的視線測量信息，確定空間目標軌道，Hippelheuser等[9]則將此方法拓展到多航天器測量場景中，并設計了多視線測量信息選擇策略。由于Li等和Hippelheuser等的方法未引入航天器間距離信息，空間目標相對軌道確定誤差收斂慢。空間目標軌道確定精度受觀測平臺和空間目標的幾何布局影響，文獻[10-11]通過選擇兩個航天器對空間目標的視線夾角為指標函數，分別采用人工勢場法和粒子群優化方法對編隊航天器接近空間目標過程中的軌跡進行優化，有效避免了編隊內航天器對空間目標測量視線重合的情況。黃靜琪等[12]則通過對觀測節點的合理布局設計，提高了軌道確定的精度以及收斂速度。

以上研究均對航天器編隊進行優化設計，以提高空間目標相對軌道確定精度，但是還存在以下兩個問題：首先，現有研究假設編隊內航天器的軌道均可設計，并未考慮部分或者全部航天器軌道運動受限的情況，與實際工程存在較大差別；其次，根據指標函數進行編隊優化的方法，多選擇以燃料消耗和視線夾角為指標函數，以編隊內航天器位置為優化變量，其指標函數和優化變量并未明確與航天器編隊幾何布局之間的關系，存在優化變量冗余和耦合的問題，進而造成優化過程求解復雜。

本文在現有研究的基礎上，重點分析主、輔航天器和空間目標三者的幾何布局與空間目標定位誤差的變化規律，得到減小空間目標定位誤差的角度條件。通過建立輔航天器相對軌道要素與該角度條件的關系，在主航天器軌道受限時，設計輔航天器初始相對軌道，結合空間目標初始相對軌道信息，采用遺傳算法對輔航天器相對軌道要素取值進行優化，提高空間目標相對軌道確定精度。

本文首先建立基于雙視線測量的空間目標相對軌道確定方法，然后研究空間目標定位誤差變化規律，之后根據這一規律設計并采用遺傳算法優化輔航天器相對軌道，最后采用數值仿真對編隊設計和優化方法進行驗證、對比和分析。

1 雙視線測量相對軌道確定方法

本文建立的雙視線測量相對軌道確定方法原理如圖1所示，主航天器C1和輔航天器C2采用光學相機分別獲取空間目標的視線信息l1和l2，主航天器通過激光雷達測量與輔航天器的基線信息r21。根據上述測量信息并結合相對軌道動力學模型，采用擴展卡爾曼濾波(Extended Kalman filter,EKF)方法，在主航天器C1的軌道坐標系下，完成空間目標相對位置和相對速度的估計。

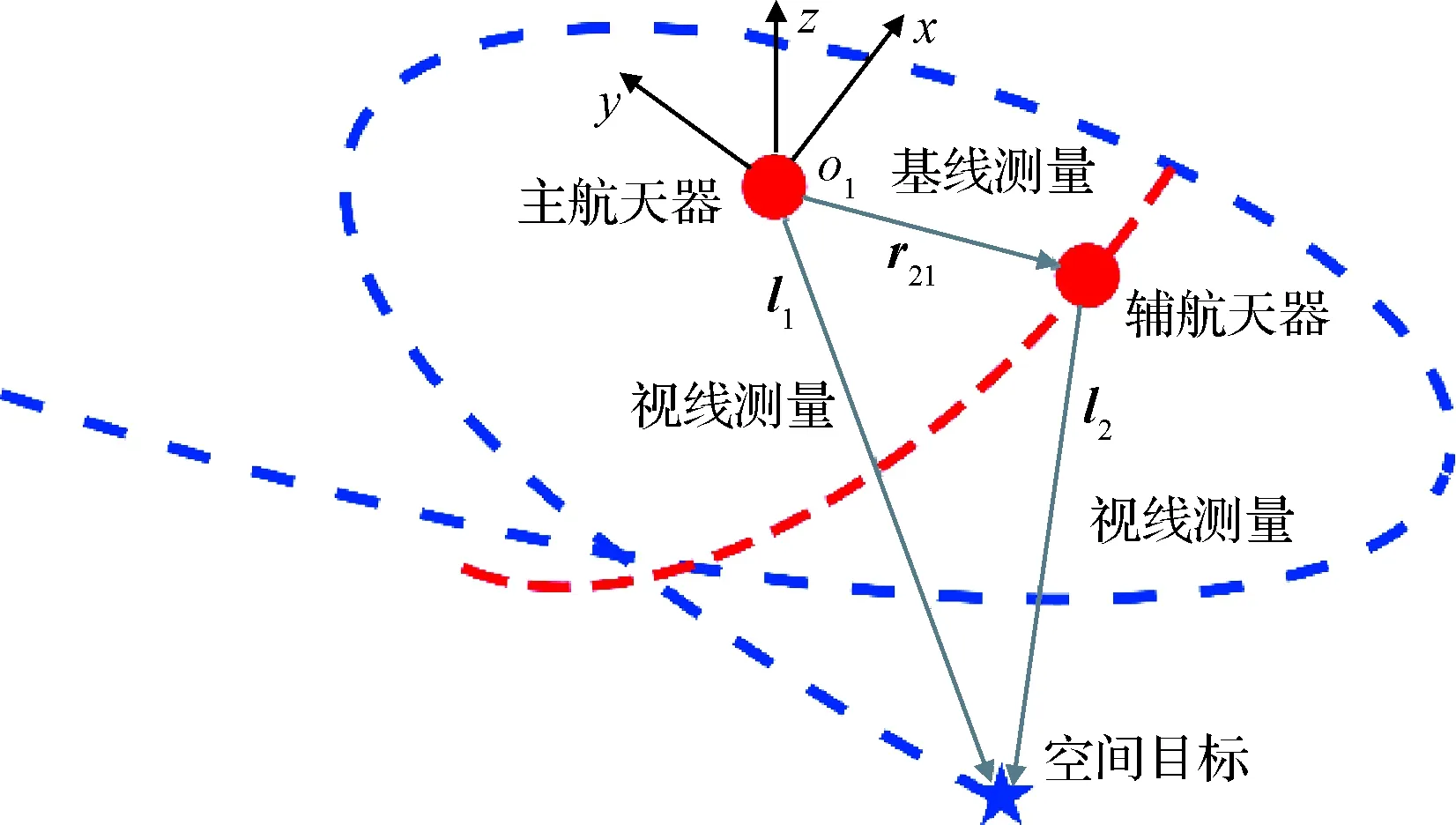
圖1 雙視線測量相對軌道確定示意圖Fig.1 Schematic of relative orbit determination by double line-of-sight measurement

在主航天器軌道坐標系中，采用CW方程描述輔航天器和空間目標的運動[6]，系統的狀態方程為

(1)

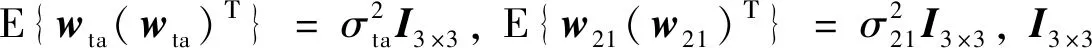
(2)

式中：n是已知的主航天器平均軌道角速度。

視線測量信息采用空間目標在主、輔航天器光學相機像平面坐標l1=[u1,v1]Τ和l2=[u2,v2]Τ表示為

(3)

式中：f1,f2為主、輔航天器搭載光學相機的焦距；[x1,y1,z1]Τ與[x2,y2,z2]Τ分別表示空間目標在主、輔航天器相機坐標系下的坐標，其與系統估計狀態之間關系為

(4)

定義系統的測量方程為

(5)

由式(1)和式(5)組成的相對軌道確定系統采用EKF方法進行融合[13]。本文接下來分析空間目標位置確定誤差與主、輔航天器和空間目標三者幾何布局之間的關系。

2 空間目標位置確定誤差分析

圖2 主、輔航天器與空間目標幾何布局Fig.2 Geometric layout of the main and auxiliary spacecraft and the space target

當主航天器與空間目標連線和基線的夾角α1，輔航天器與空間目標連線和基線的夾角α2和基線長度r21已知時，空間目標位置可表示為

(6)

式(6)說明空間目標位置確定誤差受基線測量誤差δr21和角度測量誤差δα1和δα2影響。考慮到激光雷達測距精度優于米級[14]，基線測量誤差δr21較小，并且δr21對位置確定誤差的影響遠小于δα1和δα2的影響，故可忽略基線存在的測量誤差[15]。本文中主、輔航天器基線長度r21保持1～3 km，空間目標到基線距離L在20～70 km變化，L和r21之比k在7～70之間變化，此時通過仿真和理論分析可知空間目標沿視線方向的距離不確定度要遠大于垂直視線方向的距離不確定度，可采用距離L的確定誤差來近似空間目標的位置確定誤差。綜上所述，當僅考慮角度測量誤差δα1和δα2時，有空間目標位置確定誤差

(7)

假設角度測量誤差δα1和δα2相互獨立且服從零均值高斯分布，其標準差均為σα，則有位置確定標準差σL

(8)

式(8)說明當α1+α2趨向0°或180°時，主、輔航天器和空間目標趨向于共線，雙視線測量退化為單視線測量，此時單次測量位置確定誤差σL趨向無窮。

對于某一確定的L和r21比值k，定義S(α1,α2)為誤差放大系數，表示角度測量誤差和位置確定誤差傳遞關系，與主、輔航天器和空間目標幾何布局相關，其值越小說明由角度測量誤差造成的空間目標位置確定誤差越小，有

(9)

為求解S(α1,α2)取極小值時的α1和α2之值，考慮式(6)的等式約束，建立約束優化問題

(10)

當α1=α2=α時，由式(6)可得tanα=2k，對式(9)進一步化簡有

(11)

式(11)說明，L和r21比值k越大，空間目標位置確定誤差越大。圖3表示k取不同值時，函數S(α1,α2)以α1,α2為自變量的曲線，可知對于本文中L和r21比值在7～70之間變化的場景，函數S(α1,α2)極小值點均在α1=α2處，并且k值越大其極小值越大。

圖3 不同k值下的函數S(α1,α2)曲線Fig.3 Curve of the function S(α1,α2) with different k values

綜上所述，為提高空間目標定位精度，一方面要避免主、輔航天器和空間目標共線的情況；另一方面應盡可能使空間目標與主、輔航天器基線中點連線和基線的夾角φ接近90°，并且適當增加主、輔航天器基線長度r21以減小L和r21比值k。

3 輔航天器初始相對軌道設計與優化

前文通過對雙視線測量下空間目標定位誤差變化的分析，說明在相對軌道確定過程中主、輔航天器和空間目標需滿足一定角度條件。另外，考慮到主航天器軌道運動受限，僅可對輔航天器軌道進行設計，同時為節省燃料、滿足基線測量的距離約束，輔航天器采用自然繞飛方式與主航天器保持1～3 km距離。本節通過建立輔航天器相對軌道要素與角度條件之間關系，設計滿足以上多種約束的輔航天器初始相對軌道，并采用遺傳算法對初始相對軌道進行優化。

3.1 輔航天器初始相對軌道設計

采用相對軌道要素(Relative orbital elements,ROE)描述輔航天器和空間目標在主航天器軌道坐標系中的運動[8]。相對軌道要素為[ae,xd,yd,zd,β,θ]六元數組，在主航天器軌道坐標系中，給定時間t，目標位置[x,y,z]滿足

(12)

式(12)說明，當xd=0時，目標在主航天器軌道坐標系xy平面的運動為橢圓，橢圓中心為(xd,yd)，半長軸為2ae，半短軸為ae，起始相位為β；當xd≠0，目標在主航天器軌道坐標系xy平面的投影比較復雜，可看作是一系列運動橢圓的拼接，橢圓中心(xd,yd)以速率-1.5nxd隨時間沿y軸正方向移動；目標在主航天器軌道坐標系z軸的運動是振幅為zd，初始相位為θ的簡諧振動，如圖4所示。

圖4 近圓參考軌道中的相對運動Fig.4 Example of the relative motion in a near-circular reference orbit

根據圖2中的幾何關系，空間目標與主、輔航天器基線中點連線和基線的夾角φ滿足

(13)

(14)

首先，根據空間目標運動起始時刻三軸分量特征，可將式(14)展開并化簡為

cos2φ=

(15)

式(15)說明：

1)夾角φ僅與輔航天器相對主航天器的軌道運動相關，與空間目標運動無關，因此在主航天器軌道運動受限時，可通過設計輔航天器初始相對軌道來改變夾角φ；

結合式(12)，輔航天器x，z軸分量可表示為

(16)

為保證輔航天器對主航天器形成自然繞飛軌跡，需滿足xd=0，此時輔航天器沿主航天器y軸飄移速率為0，根據三角函數公式，式(16)可化簡為

sin(2nt+λ1)

(17)

式中：

(18)

式(17)說明：

1)當ae=zd=0時，輔航天器在主航天器軌道坐標系xz平面內投影為零，主、輔航天器和空間目標共線；

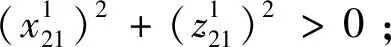
3)特別地，當cos[2(β-θ)]=1時，有

sin(2nt+λ1)

(19)

根據三角函數關系有

(20)

同理，當空間目標在主航天器下方時，式(14)可展開為

(21)

輔航天器在yz平面的投影滿足

sin(2nt+λ2)

(22)

式中：

(23)

式(22)說明：

2)特別地，當cos[2(β-θ)]=-1時，有

(24)

綜合式(17)和式(22)結論，為避免在空間目標接近過程中主、輔航天器與空間目標共線的情況，要求主、輔航天器基線在xz，yz平面投影不為零，輔航天器初始相位應滿足不等式cos[2(β-θ)]≠±1。

綜上所述，為滿足軌道確定過程中的角度條件，輔航天器相對軌道元素需滿足ae≠0,zd≠0,cos[2(β-θ)]≠±1；同時為保證主、輔航天器編隊保持穩定，輔航天器相對軌道元素應滿足xd=0，而ae,zd,yd根據主、輔航天器距離約束取值。進一步可知，不同的初始相位β和θ引起相對軌道確定過程中基線長度r21和夾角φ的不同變化，因此在基線長度滿足約束時，可通過設計初始相位來改變基線長度r21和夾角φ隨時間的變化規律，使夾角φ接近90°并減小比值k，從而減小空間目標相對軌道確定誤差。

3.2 輔航天器初始相對軌道優化

根據上節分析影響角度和距離等約束的輔航天器相對軌道要素，本節將輔航天器相對軌道要素取值求解問題轉化為優化問題。考慮到β,θ是影響相對軌道確定誤差的主要元素，同時為在滿足距離約束時增加主、輔航天器基線長度，選擇輔助航天器相對軌道元素中yd,β,θ為優化變量，ae,zd,xd相對軌道要素按設計值給定。

優化問題可表示為

(25)

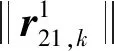
本文設計的基于遺傳算法的輔航天器初始相對軌道求解方法流程為：

1)設定種群大小、終止條件、交叉和變異等超參數；

2)對優化變量yd,β,θ采用實數編碼，并根據變量約束進行種群初始化；

3)計算種群內個體的適應度函數值J；

4)依次對個體執行選擇、交叉和變異操作；

5)判斷迭代過程是否滿足終止條件，若不滿足，則返回步驟3),若滿足則執行步驟6)；

6)返回最優個體，解碼得到最優解。

4 數值仿真與分析

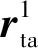
(26)

式中：r為空間目標相對主航天器的真實相對位置，仿真中可根據高精度軌道積分模型輸出的空間目標和主航天器在慣性系中的絕對位置，及主航天器軌道坐標系到慣性坐標系間的轉換矩陣計算。

表1 測量信息誤差特性Table 1 Measurement error characteristics

表2 濾波算法參數Table 2 Parameters of the filtering algorithm

測量信息誤差特性和相對軌道確定濾波算法參數設置分別在表1和表2給出。仿真中主航天器在慣性系中的軌道參數是：半長軸a為42164.16 km，偏心率e為10-4，軌道傾角i為0.001°，升交點赤經R為29.5°，近地點幅角ω為14.4°，平近點角M為59.95°。仿真中空間目標軌道參數，以及場景E1和場景E2下設計的輔航天器C2軌道參數見表3，表3中的參數值與式(12)中六元數組定義一一對應。

表3 初始相對軌道參數Table 3 Initial relative orbital elements

空間目標接近主航天器曲線如圖5所示，空間目標起始時刻y軸分量為-120 km，遠大于其它兩軸分量；當空間目標運動到主航天器正下方時，x軸分量約為-52 km，其余兩軸分量約為0 km。

圖5 空間目標相對主航天器的軌道運動Fig.5 Orbital motion of the space target relative to the main spacecraft

1) 仿真場景E1 輔航天器在主航天器軌道坐標系xy平面內運動為半長軸、半短軸之比為2∶1的橢圓運動，在xz平面、yz平面投影均為橢圓，輔航天器距主航天器軌道坐標系三軸最遠距離與ae,zd,yd設計值相關，如圖6所示。

空間目標相對位置估計誤差如圖7所示，根據第3節結論設計的主、輔航天器編隊構型，可以保證對空間目標相對位置估計的收斂性，但在估計過程中仍會出現估計誤差增大的現象，如圖7中第8小時左右出現的尖峰。此時主、輔航天器和空間目標接近共線，對應圖8中空間目標與主、輔航天器基線中點連線和基線夾角φ接近180°。

圖6 輔航天器相對主航天器的軌道運動(E1)Fig.6 Orbital motion of the auxiliary spacecraft relative to the main spacecraft (E1)

圖7中出現相對位置估計誤差增大的現象，一方面是因為輔航天器的軌道設計依據式(17)和式(22)中cos[2(β-θ)]≠±1的結論，僅考慮空間目標在起始時刻和中間時刻三軸分量特征，未考慮空間目標整個接近過程；另一方面，在設計輔航天器初始相對軌道時，式(15)做了適當簡化，并且未考慮空間目標運動信息，與實際情況存在偏差。

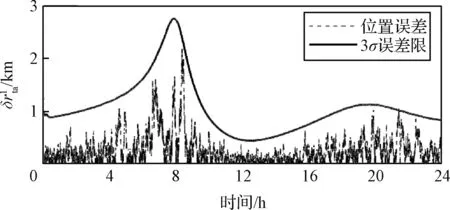
圖7 空間目標相對主航天器的位置估計誤差(E1)Fig.7 Position estimation error of the space target relative to the main spacecraft (E1)

圖8 中心夾角變化(E1)Fig.8 Variation of the center angle (E1)

2) 仿真場景E2 對比場景E2和場景E1中輔航天器運動，因為運動起始相位不同，兩場景中輔航天器在主航天器軌道坐標平面投影不同，但與各坐標軸最大距離相同，場景2中輔航天器運動如圖9所示。

圖9 輔航天器相對主航天器的軌道運動(E2)Fig.9 Orbital motion of the auxiliary spacecraft relative to the main spacecraft (E2)

空間目標相對位置估計誤差如圖10所示，在相對軌道確定過程中仍會出現誤差增大的現象，如圖10中第18小時左右出現的尖峰，同時圖11中夾角φ接近0°，主、輔航天器和空間目標近似共線。仿真場景E2中空間目標位置確定誤差增大時刻以及位置確定誤差曲線變化規律與仿真場景E1不同，說明設計輔航天器不同的起始相位對位置確定誤差的影響不同，與第3節分析結論相符。

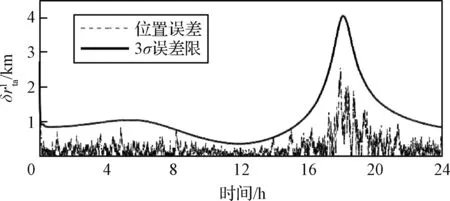
圖10 空間目標相對主航天器的位置估計誤差(E2)Fig.10 Position estimation error of the space target relative to the main spacecraft (E2)

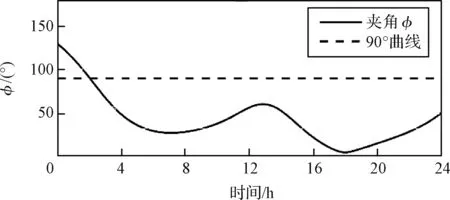
圖11 中心夾角變化(E2)Fig.11 Variation of the center angle (E2)

3) 仿真場景E3 場景E3中采用遺傳算法優化輔航天器相對軌道參數。優化后的輔航天器部分相對軌道元素為yd=-0.337 km,β=92.07°,θ=97.84°，其余相對軌道元素與前文設計值相同，分別為ae=1.25 km,xd=0 km,zd=1 km。優化后yd不為零，增加了主、輔航天器基線長度；初始相位β和θ改變了空間目標與主、輔航天器基線中點連線和基線夾角φ，以及基線r21隨時間的變化規律。

優化后輔航天器在主航天器軌道坐標系中的運動如圖12所示。相比于場景E1和場景E2設計的輔航天器初始相對軌道，因為yd不為零，輔航天器與各坐標軸最大距離和場景E1與場景E2存在一定差別，因為起始相位不同造成輔航天器運動在各平面投影與場景E1和場景E2有較大差別。

采用優化輔航天器相對軌道要素后的編隊對空間目標相對位置估計誤差如圖13所示，與圖7和圖10相比，優化后相對位置估計誤差由最大4.1 km減小到低于0.3 km，同時誤差波動較圖7和圖10明顯減小。空間目標與主、輔航天器基線中點連線和基線夾角變化平緩，并且夾角φ遠離0°和180°，可以滿足相對軌道確定過程中主、輔航天器和空間目標不共線的角度條件。

優化后主、輔航天器基線長度變化如圖15所示，在輔航天器繞飛過程中，基線在1.2 km至3 km變化。綜合圖13～圖15，在12 h處，相對位置估計誤差取最小值，此時夾角約為90°，基線長度也在極大值點附近，與式(10)分析結論相符。

圖12 輔航天器相對主航天器的軌道運動(E3)Fig.12 Orbital motion of the auxiliary spacecraft relative to the main spacecraft (E3)

圖13 空間目標相對主航天器的位置估計誤差(E3)Fig.13 Position estimation error of the space target relative to the main spacecraft (E3)

圖14 中心夾角變化(E3)Fig.14 Variation of the center angle (E3)

圖15 主、輔航天器距離變化(E3)Fig.15 Distance variation between the main and auxiliary spacecraft (E3)

5 結 論

本文為提高雙視線測量下空間目標相對軌道確定精度，分析了空間目標定位誤差與輔航天器相對軌道要素間的關系，設計并采用遺傳算法優化了輔航天器相對軌道要素。理論分析和數學仿真結果表明：空間目標和主、輔航天器基線中點的連線與基線夾角趨向90°,空間目標距離和主、輔航天器基線長度比值越小，目標定位精度越高；在主、輔航天器基線長度滿足約束時，相對軌道確定誤差受輔航天器相對軌道要素中的起始相位影響；采用遺傳算法優化輔航天器的起始相位后，主、輔航天器編隊對空間目標相對位置確定誤差由最大4.1 km減小到低于0.3 km且不超過1.2 km。本文研究要求空間目標不存在軌道機動，因此針對空間目標存在軌道機動的情況，如何設計與優化航天器編隊以提高相對軌道確定精度是下一步要研究的內容。