基于Hotelling模型的線上零售商運費險策略研究

0 引言

隨著電子商務的迅速發展，網購已成為一種普遍的購物方式。據國家統計局網站公布的數據顯示，2021年全國網上零售額130 884億元，同比增長14.1%[1]。但是由于沖動消費、商品描述失真以及商品質量問題等原因，網購的退貨率一直處于較高水平。調查顯示大部分的退貨糾紛集中在退貨的運費承擔問題上，為了減少此類問題的發生，淘寶和華泰保險于2010年聯合推出一款新型險種——運費險，即線上零售商為所售產品向保險公司投保并免費贈送給顧客，若發生退貨行為，消費者先自行墊付運費將產品退回給零售商，零售商收到貨物并確認后，保險公司向顧客支付運費理賠。線上零售商提供的運費險能有效解決消費者退貨時的運費承擔風險，提高消費者的購買意愿，但同時保費也增加了線上零售商的運營成本，因此運費險受到廣泛關注。

有許多文獻對退貨問題進行了研究。比如，Scott Davis等[2]指出MBG（Money-Back-Guarantee）作為最流行的退貨策略，零售商承諾不論任何原因退貨都將提供全額退款給消費者。Xiao等[3]發現當消費者估值增加的概率非常小時，供應鏈最好采用全額退款策略，否則供應鏈應采用不退貨策略。McWilliams和Bruce[4]建立了一個雙頭壟斷模型，研究了MBG對兩個分別銷售高質量和低質量產品的競爭零售商的影響，研究表明MBG對前者有害，對后者有益。姚忠[5]借助報童模型，建立了制造商和零售商以各自利潤最大化為目標的Stackelberg博弈模型，研究結果表明制造商適當地采用退貨策略不僅可提高供應鏈的整體利潤，也可激勵零售商降低價格，擴大訂單。黃宗盛[6]將銷售商的退款保證策略分為兩個渠道都不提供、僅實體渠道提供、僅網絡渠道提供以及兩個渠道同時提供四種，分別求解得到相應的最優定價及利潤，研究發現銷售商在實體渠道和網絡渠道的產品價格僅與其是否在該渠道提供退款保證服務有關，而與另一渠道是否提供退款保證無關，如果銷售商想要刺激某渠道的利潤水平，當退貨產品殘值較高時應選擇在該渠道提供退款保證，而當殘值較低時應選擇在另一渠道提供退款保證。

運費險自誕生以來，便發展迅速，引起了眾多學者的關注與研究。雷欣靈[7]認為運費險作為一種新險種，一經推出就受到消費者的歡迎，它歷史性地彌補了網購險缺乏的空白，使買賣雙方的矛盾得到進一步的緩解，為電子商務的發展助力。但是運費險是隨著社會發展而出現的新事物，發展不夠完善，制度設計上還有很多問題需要解決。單汨源等[8]通過構建數學模型并對比分析了賣家不提供運費險、提供運費險、消費者購買運費險三種運費險策略下線上零售商的盈利能力，證明了線上零售商提供退貨運費險服務能提高盈利能力。馬建業和孫軍[9]則利用演化博弈的方法分析了網上賣家提供運費險策略與買家退貨行為問題。Fan和Chen[10]構造了由制造商和零售商構成的兩階段供應鏈模型，分別考慮采納賣家贈送運費險和消費者購買運費險兩種運費險策略，證實當運費險保費較低、退貨運費理賠較高的情況下，零售商更傾向于選擇賣家版運費險。Lin等[11]研究了零售商面對具有不確定估值的異質消費者的最優定價和退貨策略，以及貨運保險的價值，發現零售商為消費者提供退貨運費保險的情況下，運費保險對零售商是否有利取決于單位保險費和退貨運費成本。Geng等[12]從保險公司的角度構建了數學模型，得到最優的保險定價以及理賠金額。Chen等[13]研究了零售商在轉售和代理銷售兩種模式下提供或不提供運費險，發現與轉售形式相比，代理銷售形式中的零售商需要更靈活地利用提供運費險的策略。因為隨著單位退貨損失的增加，最優策略在提供與不提供運費險之間轉換的更多。何瑩瑩和郭春香[14]研究在消費者估值不確定條件下零售商的預售策略和退貨運費險決策問題，結果發現其最優退款金額等于產品的單位采購成本，只有在退貨運費非常小時，零售商購買運費險才可能會為其帶來損失。楊雷和常娜[15]通過對比在無運費險、消費者購買運費險、賣家購買運費險三種情境下零售商、物流公司、保險公司的利潤以及消費者剩余，發現在退貨率較低的優質市場中，運費險的引入是無效的；退貨率較高時，消費者購買運費險有利于提高社會總福利。

現存文獻鮮少研究線上線下競爭環境下零售商的運費險策略選擇問題。因此，本文在前人研究的基礎上，假設線上與線下零售商向消費者銷售同一商品，在線上零售商提供和不提供運費險兩種策略下，通過構建數學模型，求解得到兩零售商的最優定價，市場需求以及最大利潤。本文主要做了以下三方面的工作：（1）在線上零售商提供和不提供運費險策略下分別構建以零售商各自利潤最大化的數學模型，推導出每個模型下的最優零售價格、需求及利潤；（2）比較了不同策略下兩零售商的定價、需求和利潤變化情況；（3）分析了保費、產品滿意度參數對利潤的影響。

1 問題描述與模型構建

本文基于Hotelling模型，假定消費者對于線下和線上銷售渠道心理偏好不同，且均勻地分布在0,[]1區間上，0和1分別代表兩個極端，不失一般性假設0端的消費者只會從線下渠道購買產品，1端的消費者只會從線上渠道購買產品。假定市場上存在一個線下零售商和一個線上零售商，用下標s表示線下零售商，下標o表示線上零售商，兩零售商相互獨立，進行古諾博弈競爭，面向同一消費者市場銷售一種無差異的產品，線下零售商與線上零售商的零售價格分別為ps和po，批發價為w。ts表示消費者從線下零售商購買產品所付出的各項成本總和，例如交通成本、時間成本等；而to表示消費者從線上零售商購買產品所付出的各項成本總和，例如付出物流等待成本、信息搜索成本等。假設消費者對該產品的估值為v，但消費者在網絡購物時只能看到零售商發布的相關描述和圖片展示，不能看到實體的產品，也不能對產品進行觸摸和感覺，還不能確定信息的真實性，因此，消費者收到網購產品后，很可能發現產品不符合自身的預期而選擇退貨，設α 0＜α＜( )1表示消費者對該網購產品的滿意率，退回的產品對于線上零售商的殘值是s，而消費者從線下零售商處購買產品不會發生退貨行為。

1.1 線上零售商不提供運費險服務（N模型）

本節假設線上零售商不提供運費險服務，用上標N表示N模型。如果消費者退貨，則需自行支付運費h。設x表示消費者對線下和線上渠道的心理偏好差異，處于位置x的消費者從線下零售商處購買商品的效用為=v-ps-tsx，從線上零售商處購買商品的效用為即xN*是N模型下消費者對線下和線上零售商心理偏好的無差異點，位于區間[0,xN*]的消費者會從線下零售商處購買商品，位于區間[xN*,1]的消費者會從線上零售商處購買商品。因此，線下零售商的市場需求：

線上零售商的市場需求：

線下零售商的利潤函數：

線上零售商的利潤函數：

證明：首先，將式（1）和式（2）分別代入式（3）和式（4）中，然后，分別求關于ps以及關于po的二階導數，因為所以得到均為凹函數，即有極大值。根據一階條件，對

1.2 線上零售商提供運費險服務（Y模型）

本節假設線上零售商提供運費險服務，為每筆訂單向保險公司支付保費c，消費者退貨時，會獲得保險公司的全額運費理賠。處于位置x的消費者從線下零售商處購買商品的效用為=v-ps-tsx，從線上零售商處購買商品的效用為=α (v-po)-to(1-x)。當是Y模型下消費者對線下和線上零售商心理偏好的無差異點，位于區間[0,xY*]的消費者會從線下零售商處購買商品，位于區間[xY*,1]的消費者會從線上零售商處購買商品。因此，線下零售商的市場需求：

線上零售商的市場需求：

線下零售商的利潤函數：

線上零售商的利潤函數：

證明：命題2的證明過程與命題1類似，此處略去。

2 比較分析

本節將比較兩個模型下兩零售商的最優零售價格、市場需求和利潤，記Δpi、ΔDi和Δ∏i（i=s或者o）分別表示線上零售商提供運費險服務和不提供運費險服務兩零售商的最優零售價格之差、市場需求之差和利潤之差，可以得到以下命題。

命題3：（1）當c＞h (1-α)時，Δps＞0；當c＜h (1-α)時，Δps＜0；（2）Δpo＞0。

由命題3可知，與線上零售商不提供運費險時相比，線上零售商提供運費險之后產品的零售價格有所提高，這是因為當線上零售商提供運費險后，其運營成本增加，為了盈利會提高零售價格。對比線上零售商是否提供運費險，線下零售商的運營成本雖然沒有變化，但是線下和線上零售商是古諾博弈競爭關系，當線上零售商的零售價格變化時，線下零售商會做出相應的價格調整。當保費較低時，線上零售商提高零售價格的幅度不大，線下零售商并沒有跟隨線上零售商一起提升零售價格，而是通過降低零售價格吸引消費者購買；當保費處于一個較高水平時，線上零售商將大幅度提高其零售價格，線下零售商就可以小幅度提高零售價格以獲得更多的利潤。

命題4：（1）當c＞h (1-α)時，ΔDs＞0；當c＜h (1-α)時，ΔDs＜0；（2）當c＞h (1-α)時，ΔDo＜0；當c＜h (1-α)時，ΔDo＞0。

命題4表明，與線上零售商不提供運費險時相比，線上零售商提供運費險之后，當保費較高時，線下零售商的市場需求增多，線上零售商的市場需求降低；當保費較低時，線下零售商的市場需求減少，線上零售商的市場需求增多。這是因為當保費較高時，線上零售商的運營成本大大增加，其零售價格上漲的幅度比線下零售商大（命題3），因為線上價格過高，導致一些線上渠道偏好者轉向線下購買，所以線上零售商的市場需求降低，線下零售商的市場需求增加；但是當保費較低時，線上零售商的零售價格只是小幅度上漲（命題3），即使線下零售商降低了零售價格（命題3），但其提供的運費險服務增加了消費者的線上購買意愿，所以線上零售商的市場需求增加，線下零售商的市場需求降低。

命題5：（1）當c＞h (1-α)時，Δ∏s＞0；當c＜h (1-α)時，Δ∏s＜0；（2）當c＞h (1-α)時，Δ∏o＜0；當c＜h (1-α)時，Δ∏o＞0。

命題5表明，與線上零售商不提供運費險時相比，線上零售商提供運費險之后，當保費較高時，線下零售商的利潤增加，線上零售商的利潤降低；當保費較低時，線下零售商的利潤降低，線上零售商的利潤增加。由命題3與命題4可知，這是因為當保費較高時，線下零售商的零售價格增加（命題3），市場需求增加（命題4），所以線下零售商的利潤增加，而線上零售商的零售價格增加（命題3），但市場需求減少（命題4），且較高的保費增加了其運營成本，所以導致線上零售商的利潤降低；當保費較低時，線下零售商的零售價格降低（命題3），市場需求降低（命題4），所以線下零售商的利潤降低，而線上零售商的零售價格增加（命題3），市場需求增加（命題4），雖然提供運費險導致其運營成本增加，但由于保費較低，增加幅度較小，所以線上零售商的利潤增加。命題5也揭示了線上零售商和保險公司實際談判時其需支付的保費c的條件：c＜h(1-α)。只有當保費低于這一閾值時，線上零售商給消費者提供運費險才有利可圖，線上零售商要努力提升與保險公司的談判能力。如果保費超過了這個閾值，將導致線上零售商自身利潤降低，而線下零售商的利潤增加，真可謂是“鷸蚌相爭，漁人得利”。

3 算例分析

本節將通過算例來分析保費c以及網購產品滿意率a對于兩零售商利潤的影響。首先研究保費對于兩零售商利潤的影響，參數設置如下：h=0.3，α=0.8，v=0.7，s=0.5，to=0.05，ts=0.1，c∈(0,0.1)。

如圖1所示，Y模型下線上零售商的利潤隨著保費的增加而單調下降，這是因為保費的增加使得線上零售商的運營成本增加，從而導致線上零售商的利潤單調下降。當保費處于較低水平時，線上零售商在Y模型下的利潤要高于N模型的利潤，但當保費到達某一閾值(h (1-α)=0.06)后，線上零售商在N模型下的利潤又要高于在Y模型下的利潤，這與命題5（2）的結論一致。

圖1 保費對線上零售商利潤的影響

從圖2可以看出，隨著保費的不斷增加，Y模型下線下零售商受到間接影響，其利潤隨之單調增加，這可以由兩零售商之間的競爭關系來解釋。當保費處于一個較低水平時，線下零售商在Y模型下的利潤比N模型下的利潤要低，但當保費超過某一閾值（0.06）后，線下零售商在Y模型下的利潤大于N模型下的利潤，這印證了命題5（1）的結論。

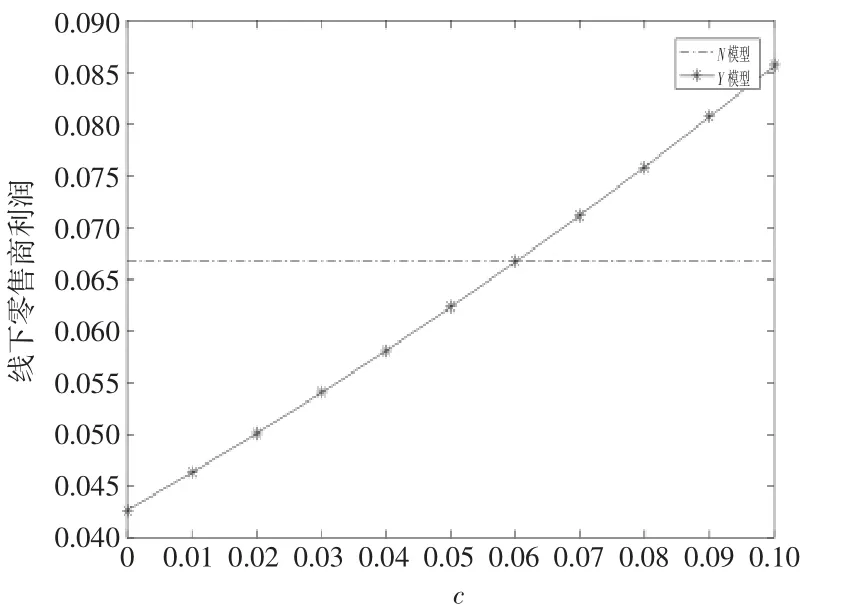
圖2 保費對線下零售商利潤的影響

其次研究網購產品滿意率對于兩零售商利潤的影響，參數設置如下，h=0.3，s=0.5，c=0.03，to=0.05，ts=0.1，α∈(0.5 ,1)。

如圖3所示，線上零售商在兩個模型下的利潤均隨網購產品滿意率的增長而單調增加，這是因為網購產品滿意率的增加會吸引更多的消費者在線上零售商處購買產品，從而導致其利潤增加。當網購產品滿意率處于較低水平時，線上零售商在Y模型下的利潤要高于N模型的利潤，當網購產品滿意率到達某一閾值(1-c/h=0.9)后，線上零售商在N模型下的利潤又要高于在Y模型下的利潤。所以，線上零售商要在網購產品滿意率較低時為消費者提供運費險服務，并在閾值范圍內努力提升其產品滿意率。

圖3 網購產品滿意率對線上零售商利潤的影響

如圖4所示，隨著網購產品滿意率的增加，在兩個模型下線下零售商受到間接影響，其利潤均隨之而單調下降，這也可以由兩零售商之間的競爭關系來解釋。當網購產品滿意率處于較低水平時，線下零售商在Y模型下的利潤要低于N模型的利潤，當網購產品滿意率到達某一閾值(1-c/h=0.9)后，線下零售商在N模型下的利潤又要低于在Y模型下的利潤。

圖4 網購產品滿意率對線下零售商利潤的影響

4 總結

本文在已有文獻的基礎上，以古諾博弈競爭的線上和線下零售商為研究對象，探究不同的運費險策略下兩零售商的最優定價、市場需求以及利潤，并作出比較分析，具體結論如下：（1）當線上零售商提供運費險后，線上零售商會提高其產品的零售價格；當保費較高時，線上零售商的市場需求減少，利潤降低；當保費較低時，線上零售商的需求增加，利潤增加。（2）當線上零售商提供運費險后，當保費較高時，線下零售商的產品零售價格增加，市場需求增加，利潤增加；當保費較低時，線下零售商的產品零售價格減少，市場需求減少，利潤減少。（3）當保費低于閾值(h ( 1-α))時，線上零售商提供運費險才有利可圖，并應在閾值范圍內努力提升其產品滿意率。

本文構建的模型是基于一定的假設條件，存在一定的局限性。在未來可以從以下幾個方面拓展：（1）本文是基于線上零售商和線下零售商進行水平古諾博弈競爭，可以進一步探討有其他企業（制造商、電商平臺、保險公司等）參與的供應鏈環境下的運費險策略；（2）本文借助于Hotelling模型構建了兩零售商的效用函數，可以進一步研究如何設計更加實際的效用函數；（3）本文是假設線上零售商免費提供運費險，實際上消費者可以根據產品特性、在線評論等，自己在購買產品的同時選擇是否購買零售商提供的收費運費險。