輪轂電機驅動電動汽車主動懸架T-S變論域模糊控制研究

李韶華， 張培強,2， 楊建森

(1.石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室，石家莊 050043；2.石家莊鐵道大學 機械工程學院，石家莊 050043;3.中汽研(天津)汽車工程研究院有限公司，天津 300300)

近年來，輪轂電機驅動電動汽車成為研究熱點，它具有結構緊湊、動力傳遞效率高、便于控制等優點，但輪轂電機使懸架簧下質量增加，會加劇車輛垂向振動。為解決該問題，主動懸架的重要性越發凸顯。在懸架控制中，車輛懸架的調節是一個多目標控制問題，對于控制策略提出了很高的要求，算法應考慮輪轂電機對平順性的負效應，保證懸架動撓度、輪胎動載荷、作動器作用力等多項因素在要求閾值之下。針對主動懸架，研究人員先后提出了神經網絡控制、MPC(model prodictive control)控制、T-S(Takagi-Sugeno)模糊控制等算法，其中T-S模糊控制結構簡單、不依賴于模型，且具有良好的動態非線性特性，引起了學者們關注[1-3]。但單一的模糊控制仍有控制精度不高，過度依賴經驗的缺點。變論域模糊控制引入伸縮因子對論域進行改變，可提高模糊控制的自適應性和控制精度，并且只對算法本身進行優化，設計方便、運行速度快，可有效改善單一模糊控制的缺點，具有很高的應用價值。

變論域模糊控制策略的關鍵在于伸縮因子的設計，柳江等[4-5]采用單個函數模型設計變論域模糊控制，取得了較好的控制效果。但單個函數模型較難反映大部分工況下伸縮因子的變化，且隨著模型的變化函數模型的參數也較難確定。針對該問題，學者們開始采用智能算法對伸縮因子進行表述，劉非等[6-7]利用模糊推理構建二級變論域模糊控制器，依靠模糊規則對伸縮因子進行表述，該方法提升了模糊控制的控制精度，且具有較好的自適應性，但用傳統的Mamdani模糊策略設計伸縮因子，仍具有輸入量較小時優化不明顯，反應速度較慢等問題。龐輝等[8]利用神經網絡設計T-S模糊控制器的伸縮因子，取得較好的控制效果，但只考慮了輸入伸縮因子的變化，且缺少試驗論證。

為了研究輪轂電機質量對分布式驅動電動汽車懸架的影響，本文分別建立了考慮和不考慮輪轂電機質量的1/4車輛主動懸架模型，研究輪轂電機質量對懸架的影響，進而針對輪轂電機驅動電動汽車的主動懸架設計一種T-S變論域模糊控制器。該控制器基于二級變論域模糊控制器思想，改進伸縮因子的設計方法，利用T-S模糊策略對輸入和輸出伸縮因子同時進行描述，從而實現車輛運行過程中控制器的變論域和自適應。最后，通過仿真及硬件在環試驗與單一模糊控制和傳統Mamdani變論域模糊控制進行對比，從而驗證了所設計控制策略的有效性。

1 車輛主動懸架動力學模型

1.1 1/4車輛模型

針對分布式驅動電動汽車建立兩自由度1/4車輛模型，如圖1所示。其中：M0為輪轂電機質量；M1為車輛的非簧載質量；M2為車輛的簧載質量；K1為輪胎的剛度，忽略阻尼；K2為懸架的剛度；C0為懸架的阻尼；X0，X1，X2分別為路面激勵、非簧載質量垂向位移和簧載質量垂向位移。考慮到作動器會產生故障，為保證車輛的安全，該模型在被動懸架的基礎上加裝作動器F以提高車輛行駛中的安全性。

懸架系統動力學方程為

(1)

(2)

車輛模型參數如表1[9]所示。

表1 車輛懸架參數

1.2 輪轂電機質量對車輛垂向振動的影響分析

為探究懸架模型中輪轂電機質量對車輛垂向振動影響，在圖1的模型中忽略輪轂電機質量M0，建立了不考慮輪轂電機質量的1/4懸架模型。通過仿真對比B級隨機路面下兩種模型的響應，如圖2所示。

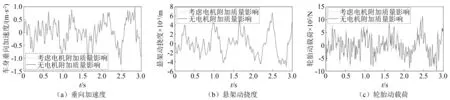
圖2 B級隨機路面下的車輛響應Fig.2 The vehicle responses on B-classrandom road

兩種模型下的車身垂向加速度均方根值、懸架動撓度和輪胎動載荷均方根值，如表2所示。

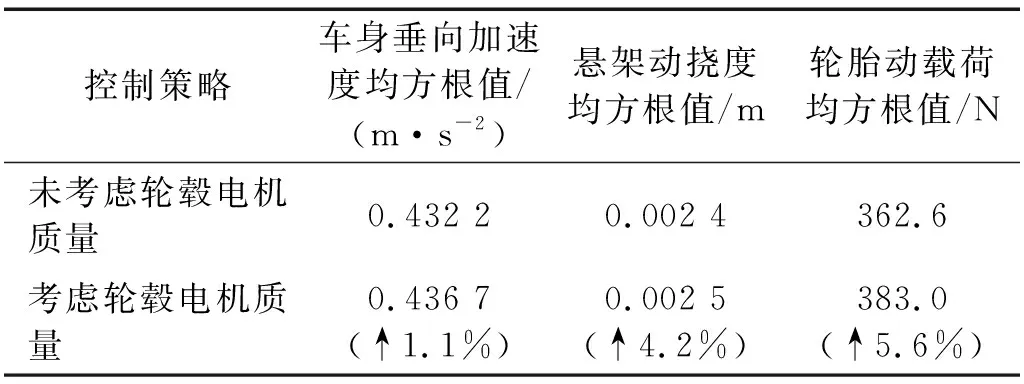
表2 B級隨機路面下各懸架平順性比較

由圖2及表2可知：考慮輪轂電機質量后，各響應指標均有所增大；輪轂電機質量對輪胎動載荷和懸架動撓度的影響大于對車體垂向加速度的影響。因此，對于分布式驅動電動汽車的懸架振動和控制研究，輪轂電機質量不容忽視。

2 T-S模糊控制器設計

相對于傳統的Mamdani模糊控制，T-S模糊控制更適合在動態非線性系統或局部線性系統中為不同工作狀態下的多線性控制器進行平滑切換，并且輸出為清晰值或為輸入量的函數，可直接作用于控制器，具有運行速度快，控制更精準的優勢。

2.1 T-S模糊算法概念

在模糊控制理論中，對于多輸入、單輸出的系統，可以利用模糊條件語句“Ifx1isA1andx2isA2，thenuisU”來進行描述，其中A1，A2為輸入系統的隸屬函數集，輸出量U則為x1，x2的線性函數f(x1，x2)。

輸出函數f(x1，x2)主要有兩種表現形式：① 0階T-S模糊推理：“Ifx2isA1andx2isA2，thenu=k”；② 1階T-S模糊推理：“Ifx2isA1andx2isA2，thenu=p*x1+q*x2+r”。其中k,p,q,r均為常數，一般通過大量數據測試和經驗得出[10-11]。

2.2 控制器設計

選取車身垂向加速度為控制目標，考慮到隨機路面的變化情況，將車身垂向速度與加速度構成一個雙輸入、單輸出的控制模型，控制框圖如圖3所示。圖3中，r與a分別為理想加速度和實際加速度輸出，ec=r-a，e為速度的誤差，ec為加速度的誤差。

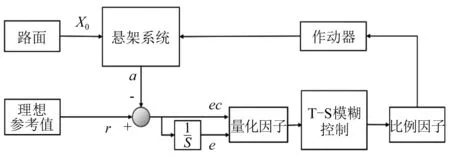
圖3 T-S模糊控制框圖Fig.3 The diagram of T-S fuzzy control

T-S模糊控制器設計步驟如下。

步驟1論域的選擇：由表1的懸架參數，搭建被動懸架，觀測車輛響應，根據各路面下的輸出，我們可以確定e和ec物理論域的范圍分別為{-0.1,0.1}和{-1.5,1.5}；

步驟2輸出函數的設計：輸出u使用0階模糊推理；

步驟3規則的建立：輸入變量為e與ec，均采用了7個語言模糊子集{NB(負大),NM(負中),NS(負小),Z(零),PS(正小),PM(正中),PB(正大)}，為保證算法可以平滑過渡，其隸屬函數均為trimf形；

步驟4量化因子Ke，Kec和比例因子Ku的選取：可根據不同路面條件下的模糊控制器的模糊論域N和系統的物理論域X進行計算[12-14]，該控制器中e的模糊論域為Ne=[-ne,ne]，ec的模糊論域為Nec=[-nec,nec]，u的模糊論域為Nu=[-nu,nu]，輸入的物理論域為Ue=[-ue,ue]和Uec=[-uec,uec]，輸出物理論域為U1=[-u1,u1]。可得

Ke=ne/ue

(3)

Kec=nec/uec

(4)

Ku=u1/nu

(5)

本文設計的T-S模糊控制器的模糊推理規則共49條，如表3所示。

表3 T-S模糊控制規則表

2.3 約束條件

主動懸架控制策略還要滿足以下約束條件：①保證車輛的平順性，該要求一般選取車身的垂向加速度作為評價指標，本文以降低車身垂向加速度為主要目標；②考慮到懸架本身結構的設計，為保證車輛各部件的運行不受干擾，控制器應保證懸架動撓度保持在一定的行程范圍Xmax內，減少懸架與限位塊碰撞概率，即

|X2-X1|≤Xmax

(6)

為了保證車輛的行駛安全和操縱穩定性，在車輛行駛過程中的任意時刻，輪胎動載荷應小于車輛靜載荷[15-16]，以減少車輪與路面之間的沖擊，即

K1(X1-X0)≤(M1+M2)g

(7)

為了保證系統的穩定性和安全性,必須考慮控制器的飽和度,其輸出力應低于所規定的閾值,本文選擇直線電機作為執行機構，即

|u|≤umax

(8)

本文選取Xmax=0.05 m,(M1+M2)g=7 800 N,umax=300 N。

3 T-S變論域模糊控制器設計

車輛行駛過程中經歷的多種工況，會導致車輛垂向加速度在較大的范圍內產生變化，而上節提出的單一T-S模糊控制器面對復雜工況時則具有一定的局限性，固定的輸入、輸出論域不能充分發揮模糊控制的效果，尤其對于超出論域表述范圍的輸入，會導致輸出幅值較為振蕩，而對于過小的輸入，也不能充分利用整個論域的控制規則。為改進控制策略的工況自適應能力，引入變論域思想。

假定模糊控制器輸入和輸出的原始論域分別為

X1=[-E1,E1]
X2=[-E2,E2]
Y=[-U,U]

(9)

原始論域的范圍由輸入e和ec的值x1，x2和輸出u的值y界定，引入變論域思想后，該論域則會隨著輸入和輸出值的變化而變化，記為

X1=[-α1(x1)E1,α1(x1)E1]
X2=[-α2(x2)E2,α2(x2)E2]
Y=[-β(y)U,β(y)U]

(10)

式中，α和β為論域的伸縮因子，是一個隨著輸入量x和輸出值y的變化而不斷變化的值，α為輸入伸縮因子，β為輸出伸縮因子，當模糊控制中的輸入量和輸出量分別與伸縮因子α和β結合時，論域可以跟隨系統的輸入輸出而變化，提升系統控制的適應能力[17-18]。

變論域模糊控制策略的關鍵在于對輸入、輸出伸縮因子進行設計，輸入伸縮因子的主要作用是將系統輸入e，ec與模糊論域進行適配，使得系統輸入能充分利用模糊規則，提高控制精度。輸出伸縮因子的主要作用是調節控制器的輸出，保證輸出的穩定性。算法在設計時應考慮系統輸入e，ec的作用和權重，用T-S模糊控制規則對輸入輸出伸縮因子進行調整，滿足變化時的e和ec對系統論域的不同要求，以實現模糊論域的自我調整。

由此提出輸入伸縮因子的設計規律，其模糊控制原則為:

(1)當輸入e和ec的值均較大時，應盡快消除誤差，此時輸入論域應該擴大，保證輸入值可以有效利用模糊論域。

(2)而e和ec的值較小時，系統開始趨近于穩定，此時應考慮到e和ec兩者之間的關聯，縮小輸入系統的論域，使控制器精度提升。

(3)當e和ec的值在控制器的論域范圍內時，使論域保持不變。

根據輸入e和ec的值，同時結合T-S模糊控制器的模糊規則，可設計輸出伸縮因子的調節規律為:

(1)當e和ec較大且方向相同時，系統的誤差較大且誤差仍在不斷增大，需要系統提供大的控制量，減小其誤差，保證系統的穩定性，因此應擴大輸出論域。

(2)當e和ec較大且方向相反時，系統的誤差較大且誤差在不斷減小，需要系統盡量保證控制量不要過大，使系統的誤差減小，并保證系統不會產生較大振蕩，因此應小幅度壓縮輸出論域，保證控制力的輸出穩定。同時根據控制器的模糊規律，對控制力較小的地方輸出論域可以保持不變，防止振蕩。

(3)當e和ec較小時，系統開始趨近于穩定，應減小輸出力，即壓縮系統的輸出論域。

(4)當ec接近零而e很大且同向時，系統的誤差非常小，但系統正以很快的速度偏離設定值，此時控制量應增大以抑制系統偏離的趨勢，且要防止振蕩的產生，因此輸出論域應有小幅度擴張。

由此可提出主動懸架T-S變論域模糊控制策略，根據不同時刻e和ec的大小，通過T-S模糊控制規則推理計算出論域伸縮因子，在論域伸縮因子與量化因子和比例因子結合后，根據輸入輸出值來調整自身論域的大小，控制框圖如圖4所示。

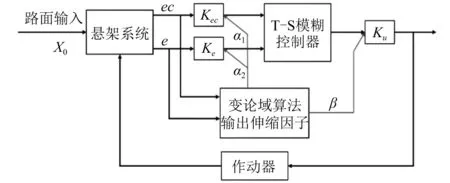
圖4 主動懸架T-S變論域模糊控制原理圖Fig. 4 The principle of T-S variable domain adaptive fuzzy control for active suspension

輸入及輸出伸縮因子模糊計算中，選取e和ec論域范圍分別為{-0.1,0.1}和{-1.5,1.5}，采用7個語言模糊子集{NB(負大),NM(負中),NS(負小),Z(零),PS(正小),PM(正中),PB(正大)}，其隸屬函數均為trimf形。輸出u為0階模糊推理輸出函數，論域的范圍為[0,1]，模糊劃分為{Z(零),S(小),M(中),B(大)}。輸入論域伸縮因子α1和α2的模糊控制規則如表4和表5所示。輸出論域伸縮因子β的模糊控制規則，如表6所示。

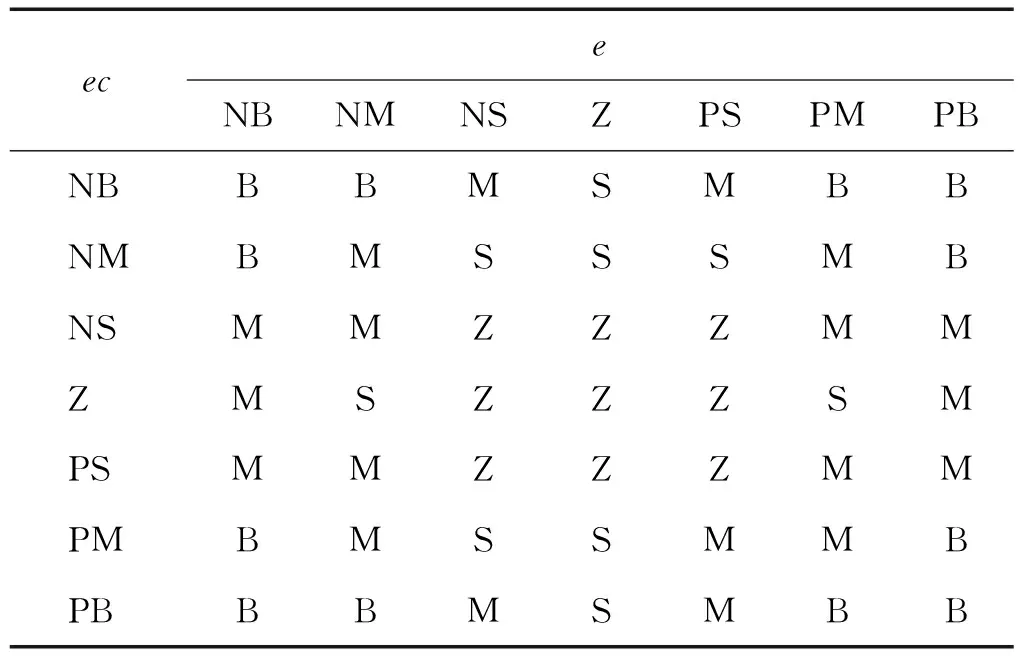
表4 輸入論域伸縮因子α1模糊控制規則表

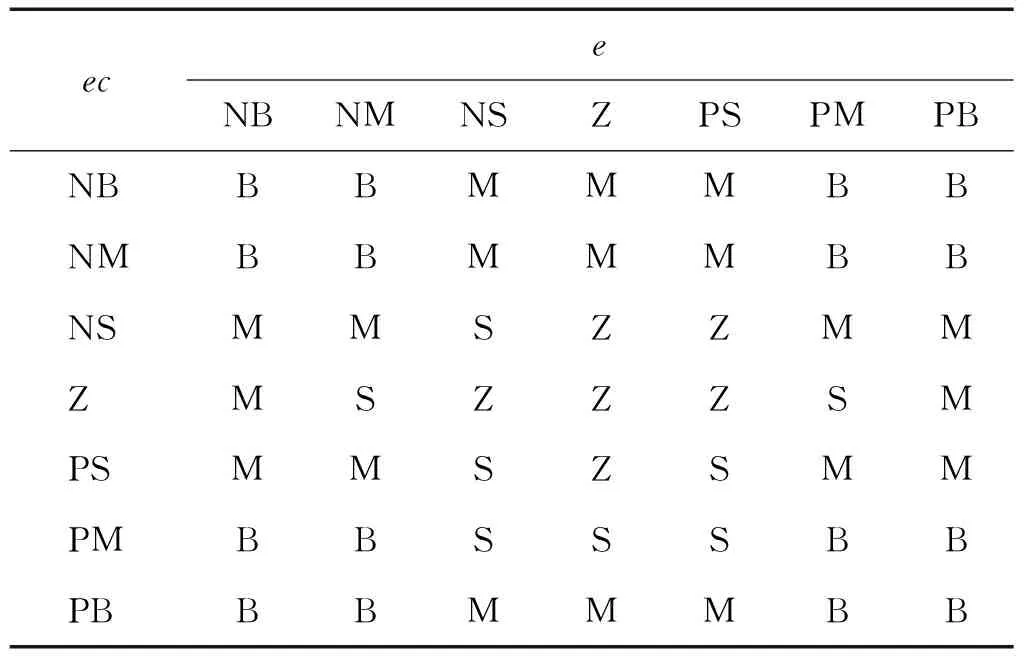
表5 輸入論域伸縮因子α2模糊控制規則表

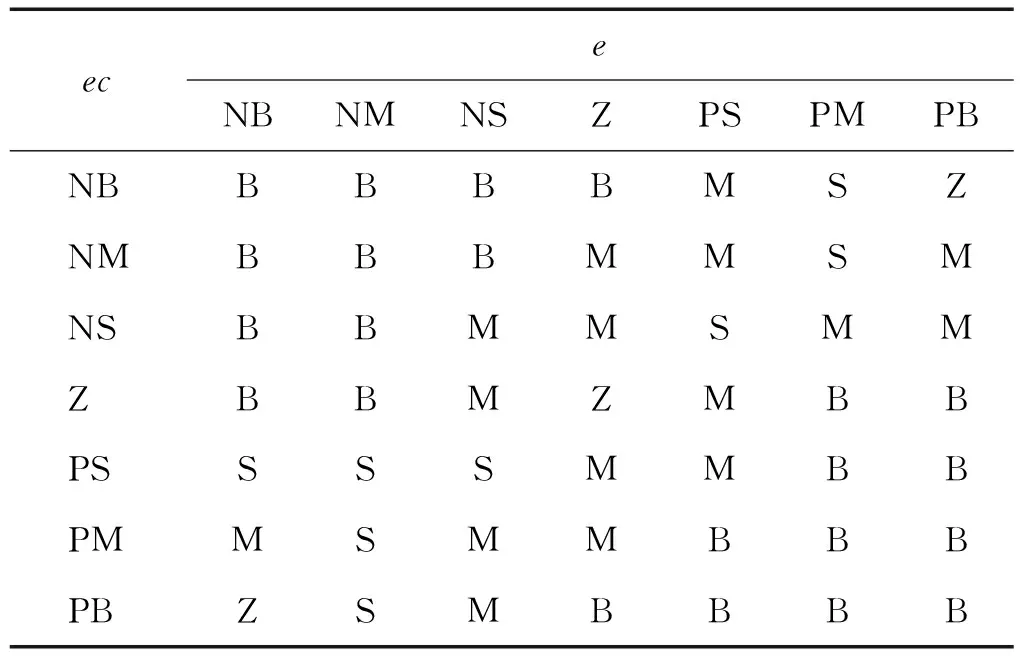
表6 輸出論域伸縮因子β模糊控制規則表

由于輸入輸出因子的e與ec的模糊劃分相同，結合3個表格的模糊規則，設計一個雙輸入三輸出的T-S模糊伸縮因子控制器，實現對輸入輸出論域的調節。

4 仿真分析

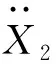
4.1 隨機路面

4.1.1 B級隨機路面

基于路面不平度的功率譜密度，使用有理函數濾波白噪聲生成法計算路面不平度[19]，取B級隨機路面，車速設定為20 km/h，行駛時間為10 s，路面激勵可由式(11)計算

(11)

式中：v為車速；Gq(n0)為路面不平度系數；w0(t)為白噪聲；q(t)為路面位移激勵。計算得到B級路面下不同控制器對懸架系統響應的影響，如圖5所示。

不同控制策略下的主動懸架與被動懸架的車身垂向加速度、懸架動撓度及輪胎動載荷均方根值，如表7所示。

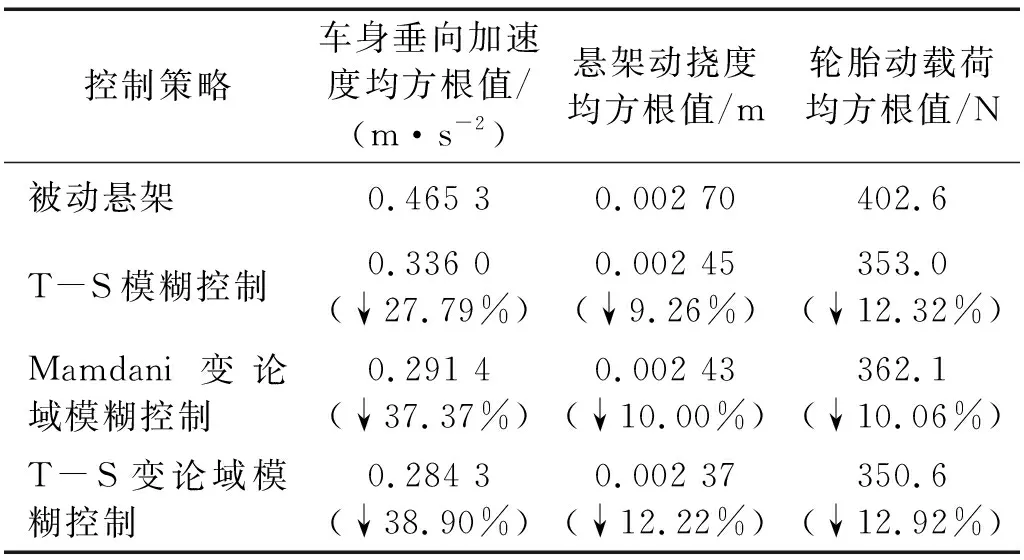
表7 B級隨機路面下各懸架平順性比較

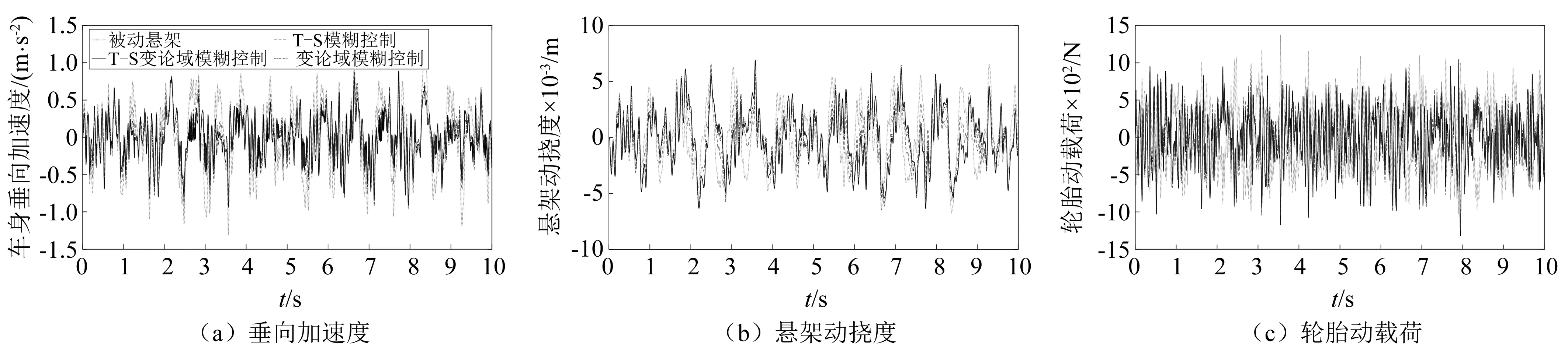
圖5 B級隨機路面下車輛響應Fig.5 The vehicle responses on B class random road

由圖5及表7可知：①T-S變論域模糊控制可有效降低車身垂向加速度，控制效果略優于其他對比算法。②各種主動控制策略對懸架動撓度和輪胎動載荷的控制效果相差不大，都可以滿足約束條件，減少懸架與限位塊碰撞及車輪與路面之間的沖擊。

4.1.2 C級隨機路面

取C級隨機路面，車速設定為20 km/h，行駛時間為10 s，計算得到C級路面下不同控制器對懸架系統響應的影響，如圖6所示。各響應的均方根值，如表8所示。

圖6 C級隨機路面下車輛響應Fig.6 The vehicle responses on C class random road

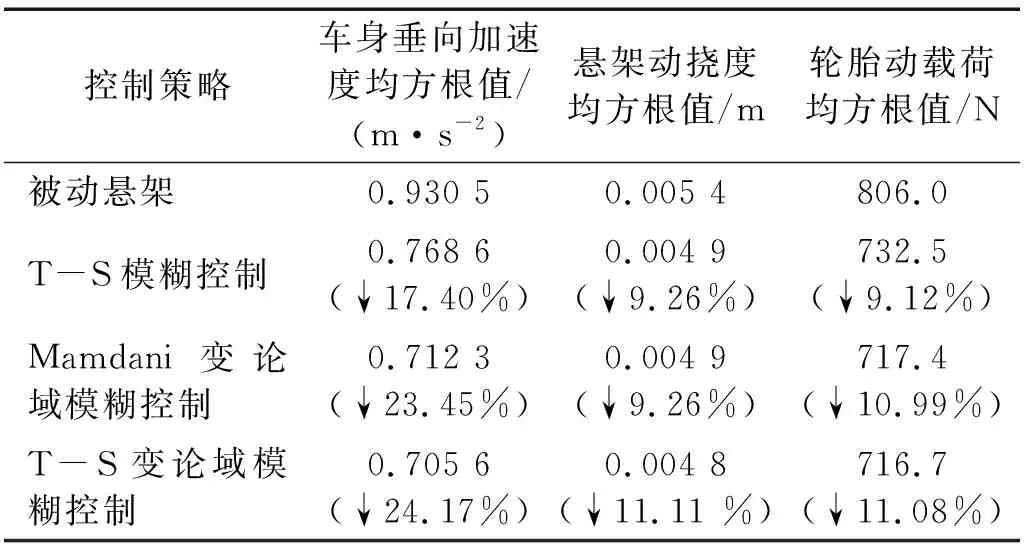
表8 C級隨機路面下各懸架平順性比較

由圖6及表8可知，在C級路面上，T-S變論域模糊控制仍可有效降低車身垂向加速度，并保證其他參數滿足約束條件，總體來看控制效果略優于其他對比算法。

4.2 對接路面

為了進一步驗證控制策略的工況自適應性，使用有理函數濾波白噪聲生成B-C級對接路面。車速設定為20 km/h，行駛時間為10 s，車輛前5 s為在B級路面上行駛，后5 s為在C級路面上行駛。仿真得到車輛響應，并與被動懸架、T-S模糊控制策略和Mamdani變論域模糊控制進行對比，如圖7所示。不同控制策略下的車身垂向加速度、懸架動撓度和輪胎動載荷均方根值，如表9所示。

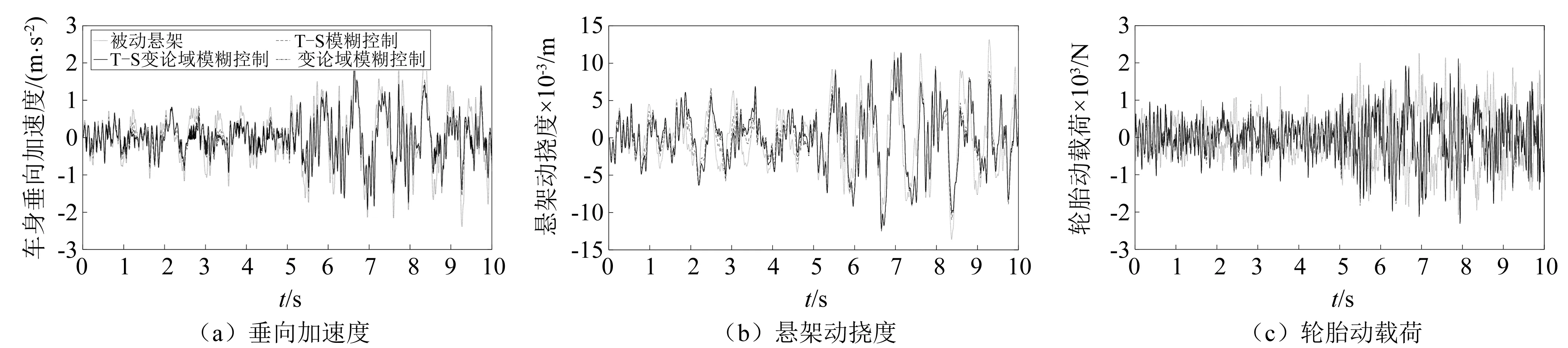
圖7 對接路面下車輛響應Fig. 7 The vehicle responses on joint road

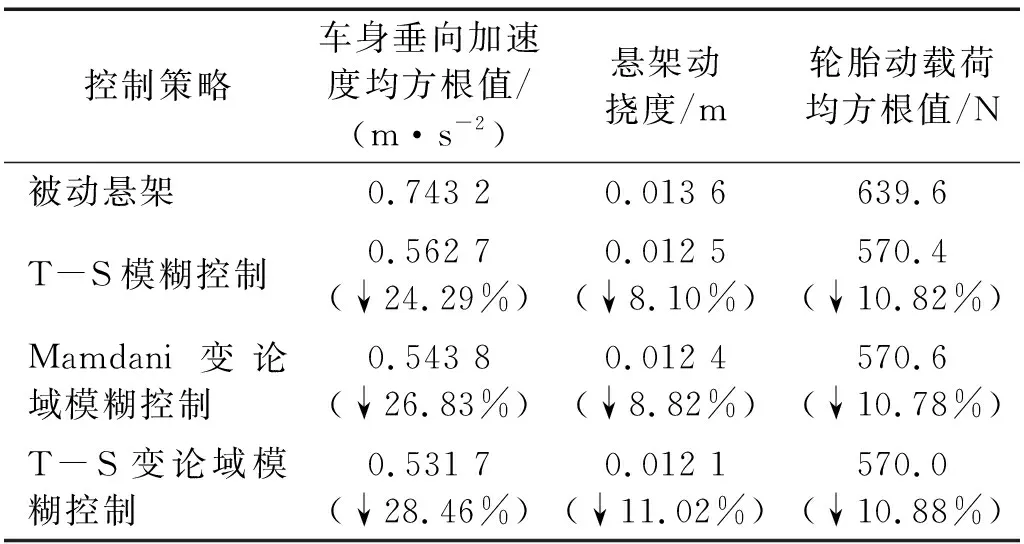
表9 對接路面下各懸架平順性比較

由圖7和表9可知，T-S變論域模糊控制的效果在變路面激勵下可顯著提高車輛平順性，并保證懸架動撓度、輪胎動載荷等多項因素在要求閾值之下。

對比B級、C級隨機路面和B-C級對接路面工況下的響應結果，可以看出：T-S變論域模糊控制在各路面下均具有很好的自適應性，控制效果均優于單一模糊控制；在對接路面等復雜工況下，相對于傳統Mamdani變論域模糊控制， T-S變論域模糊控制具有更好的控制效果。因此，所提出的T-S變論域模糊控制具有較強的工況自適應性，更適用于變路面工況。

5 試驗驗證

為了驗證T-S變論域模糊控制策略的有效性，采用加拿大Quanser公司生產的主動懸架控制試驗系統進行驗證。Quanser主動控制試驗系統是一個小型的1/4 汽車懸掛系統模型，可用于閉環系統的性能分析，配合實時軟件QuaRC，通過Simulink 庫內嵌入QuaRC軟件的特有模塊庫，對硬件端口進行通道選擇指定和實時通訊控制。在PC端通過Simulink庫編寫控制程序，通過板卡和功放器，使試驗臺在輸入的激勵和算法控制下工作，并將信號和數據傳遞回PC，其工作原理及測試現場如圖8和圖9所示。

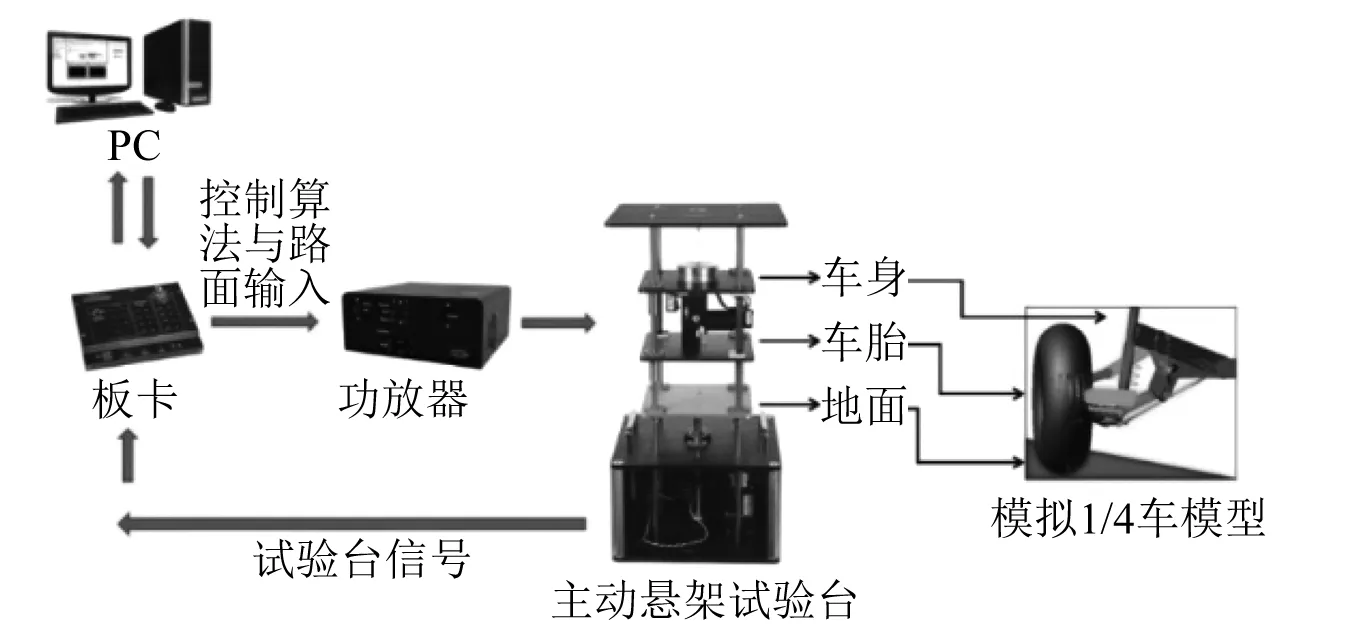
圖8 Quanser試驗臺工作原理Fig.8 The principle of Quanser test bench

由于試驗臺的硬件限制，對輸入信號的頻率和幅值有一定的要求，需要將輸入信號經由濾波后轉為試驗臺的輸入，且輸入幅值不能過大。因此，本章采用試驗臺的參數建立懸架模型并進行控制算法驗證。試驗臺參數，如表10所示。

表10 試驗臺懸架參數

5.1 隨機路面

為保證輸入相同，仍使用有理函數濾波白噪聲生成B級隨機路面模型，車速設定為20 km/h，行駛時間為10 s，經過濾波處理后作為試驗臺的輸入。實測的懸架響應，如圖10所示。

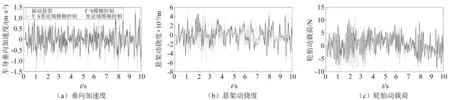
圖10 B級隨機路面下實測響應Fig. 10 The test responses on B class random road

各控制策略下懸架試驗臺的車身垂向加速度均方根值、懸架動撓度和輪胎動載荷均方根值，如表11所示。

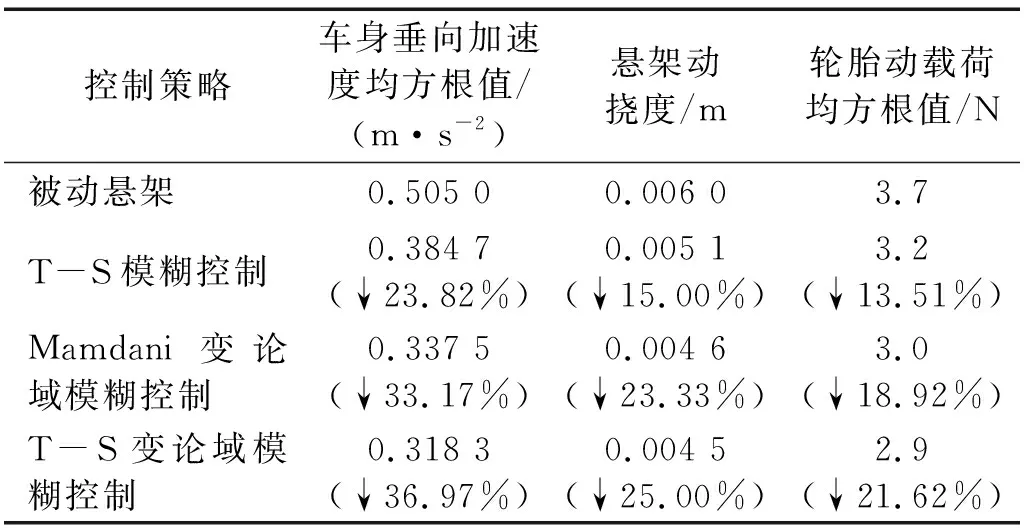
表11 試驗臺在隨機路面下懸架平順性比較

由圖10和表11可知，試驗臺得到的控制效果與仿真結果具有相同的趨勢，說明T-S變論域模糊控制在保證車輛接地安全性的前提下，可以有效改善車輛平順性，且控制效果略優于其他兩種控制策略。

5.2 對接路面

由于試驗儀器的局限性，對接路面設為A-B級對接路面，車速設定為20 km/h，行駛時間為10 s，前5 s為在A級隨機路面上行駛，后5 s為在B級隨機路面上行駛，試驗結果如圖11所示。

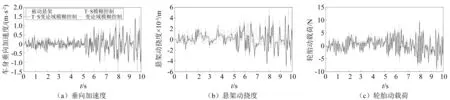
圖11 對接路面下實測響應Fig.11 The test responses on joint road

在對接路面激勵下，采用各控制器的車身垂向加速度均方根值、輪胎動載荷和懸架動撓度，如表12所示。

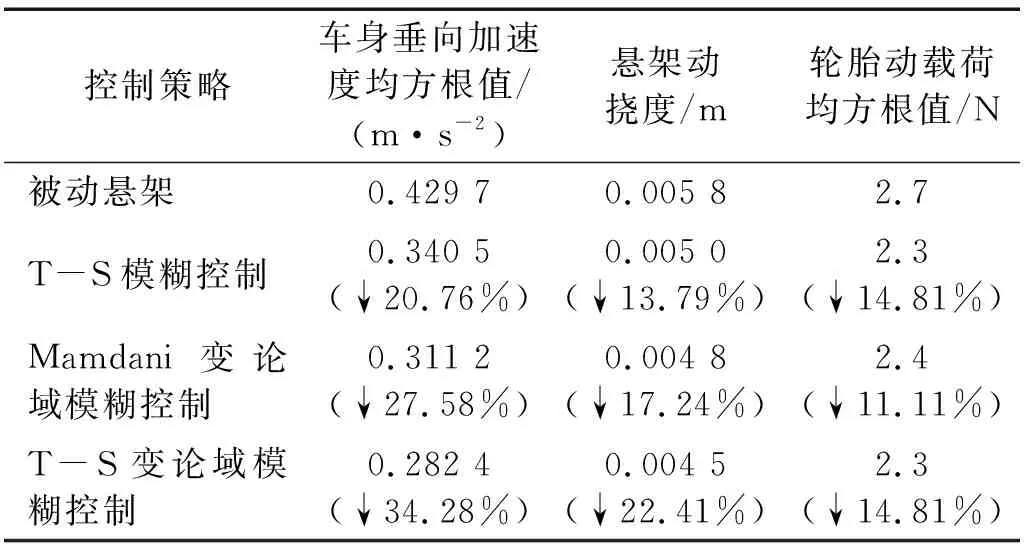
表12 試驗臺在對接路面下懸架平順性比較

由圖11和表12可知，T-S變論域模糊控制在對接路面上可以有效改善車輛行駛平順性，且控制效果均優于其他兩種控制策略。T-S變論域模糊控制在車身加速度控制上表現較好，在懸架動撓度和輪胎動載荷上表現類似于仿真試驗中的結果趨勢，即在約束指標上也有一定的控制效果。

6 結 論

本文探究了輪轂電機質量對懸架的影響，并將T-S模糊控制與變論域思想相結合，針對分布式驅動電動汽車主動懸架設計了一種新型T-S變論域模糊控制策略，仿真和臺架試驗研究表明：

(1)所提出的T-S變論域模糊控制，可以在減少輪轂電機對車輛平順性影響的基礎上，保證懸架動撓度、輪胎動載荷等多個指標在要求閾值之下。T-S模糊變論域控制在B級路面下使垂向加速度、懸架動撓度和輪胎動載荷分別降低38.9%，12.22，12.92%；在C級路面下，3個指標分別降低24.17%，11.11%，11.08%；而在B-C級路面下，3個指標分別降低28.46%，11.02%、10.88%。

(2)在各路面條件下，所提出的T-S變論域模糊控制對車身垂向加速度的控制效果均優于單一T-S模糊控制和Mamdani變論域模糊控制，并且在變路面條件下T-S變論域模糊控制的工況自適應性更突出。

(3)利用T-S模糊策略設計伸縮因子，實現論域變化,相比于傳統的Mamdani變論域模糊策略，可借助T-S模糊具有的局部線性化優勢來提升伸縮因子的變化精準度，從而使論域的變化更準確、精度更高，提升模糊控制的控制效果和運算速度和在各工況下的自適應能力。