網格與圓作圖新題
?天津南開日新學校 耳 潔 張樹義
在近幾年的各地考試中有一種與網格和圓有關的作圖題,這類題綜合性強,層次高,能很好考查學生綜合運用數學知識解決問題的能力.這類題常以壓軸題出現,由于題型新,因此可參考的題目并不多.筆者新編了一些網格與圓相結合的作圖題,給出題目的分析、解答和涉及的知識點,供大家教學時參考,不妥之處,懇請大家指正.
1 網格面積問題
“網格面積”類作圖問題可涉及:作一個圖形,其面積等于已知數值;作面積最大、最小的圖形;把一個圖形分成有一定要求的兩部分;等等.
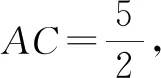
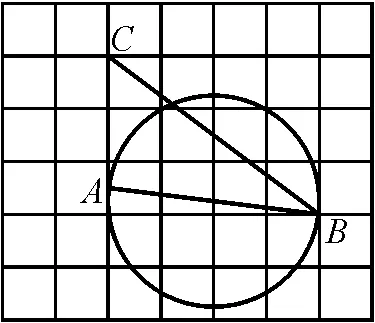
圖1
分析:不難算出△ABC的面積為5,可知△ABP的面積是△ABC面積的一半,則考慮作△ABC的中位線與圓交于點P.
解:如圖2,取格點D,E,連接DE交網格線于點F.取格點G,連接FG交AC于點H.設BC與網格線交于點M,作射線HM與圓交于點P,連接AP,BP,則點P即為所求.
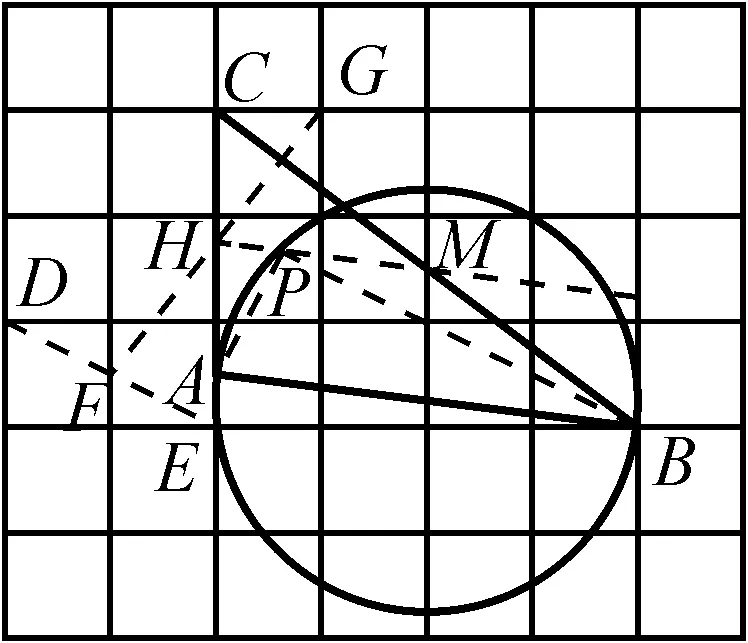
圖2
涉及知識點: ①三角形中位線性質; ②平行線間的距離 ; ③網格作圖基本動作——比例分線段.
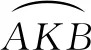
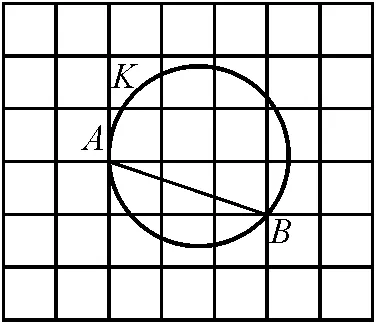
圖3
解:如圖4,取格點C,D,連接CD交AB于點E.取格點F,G,H,N,連接FG,HN,兩線段相交于點M.連接EM與圓交于點P,連接AP,BP,則點P即為所求.
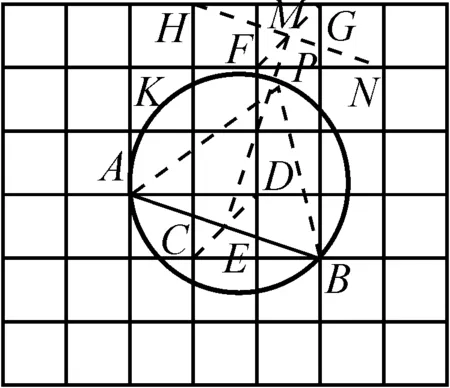
圖4
涉及知識點:①垂徑定理的推理; ②網格作圖基本動作——比例分線段; ③網格作圖基本動作——畫已知線段的垂線.
2 網格角度問題
“網格角度”類作圖問題可涉及:作一個角等于適當角度;平分已知角;作一個角等于一個角的幾倍;平分弧;弧的倍分;等等.

圖5
分析:如圖6,延長線段AB至格點E,延長線段BA至格點F,則∠FAC=45°,故∠CAB=135°.所以作∠EAM=∠MAN=∠NAC=45°即可.
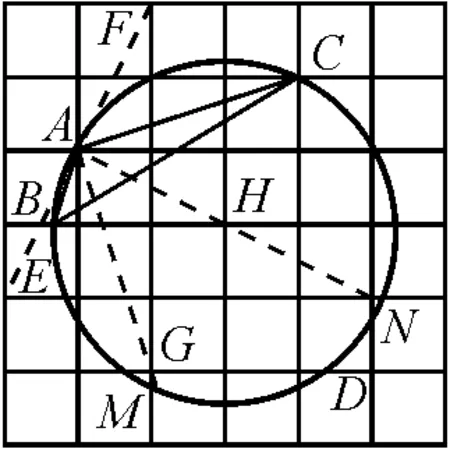
圖6
解:如圖6,取格點G,連接AG并延長交圓弧于點M.取格點H,連接AH并延長交圓弧于點N.點M,N即為所求.
涉及知識點: ①圓周角定理的推論;②等腰直角三角形的判定與性質;③網格作圖基本動作——畫指定大小的角或作角的平分線.
3 網格線段問題
“網格線段”類作圖問題可涉及:作兩條線段相等;找圓心;作切線;將軍飲馬問題;胡不歸問題;阿氏圓問題;作最長、最短的線段;等等.
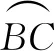
圖7
解:如圖8,取格點H,G,連接GH交AB于點M.取格點N,連接NH交AC于點F,連接MF交AD于點E.點E,F即為所求.
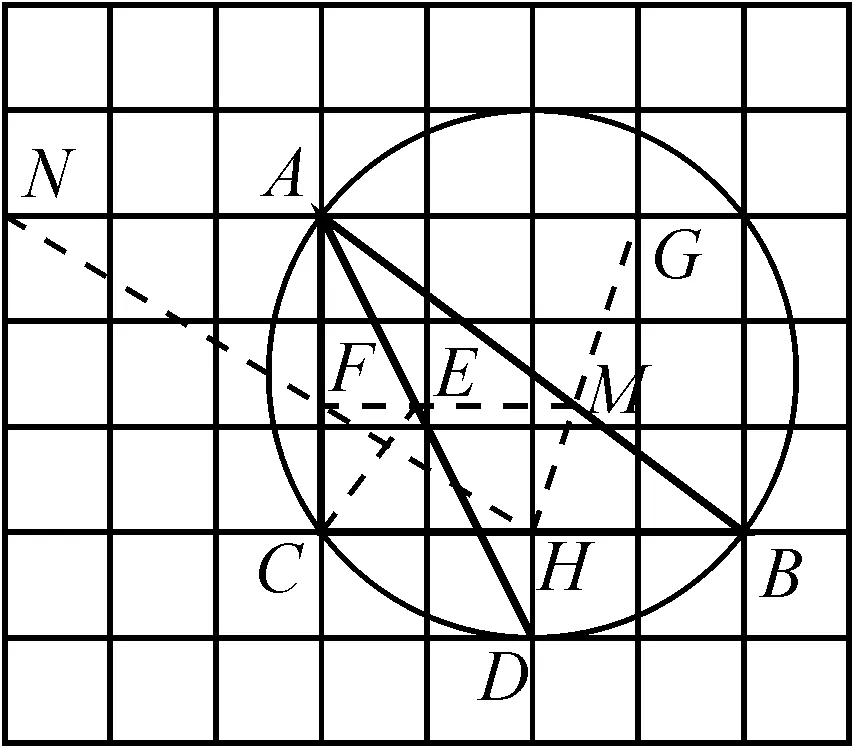
圖8
涉及知識點:①圓周角定理的推論;②全等三角形的判定與性質;③最短路徑問題,即垂線段最短;④網格作圖基本動作——比例分線段;⑤網格作圖基本動作——畫已知線的垂線(或平行線).
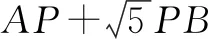
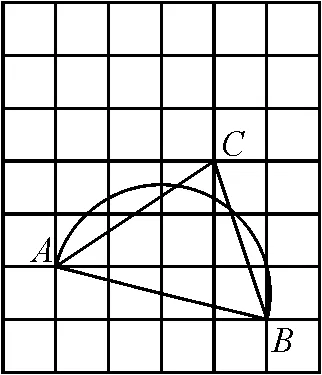
圖9
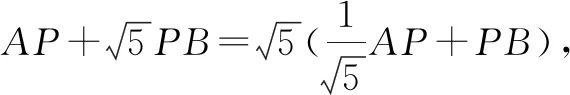
解:如圖10,取格點D,連接CD交網格線于點E.連接AE交半圓于點F.連接BF交AC于點P,點P即為所求.
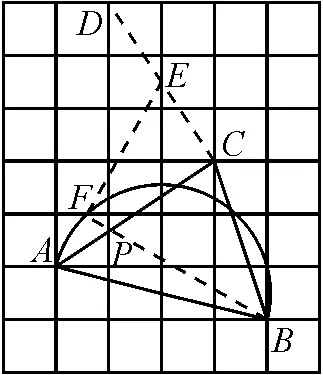
圖10
涉及知識點:①最值,即胡不歸問題;②相似三角形的判定和性質;③網格作圖基本動作——畫已知線的垂線(構造等腰直角三角形);④網格作圖基本動作——比例分線段.
例6如圖11,將△ABC放在每個小正方形邊長為1的網格中,點A,B,C均落在格點上,動點P到點A的距離為2,點Q是線段BP的中點,連接線段CQ,當線段CQ最小時,在圖中用無刻度的直尺畫出點P和點Q,并簡要說明畫法.
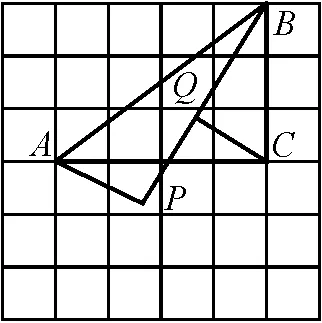
圖11
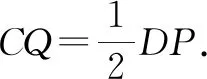
解:如圖12,取格點D,連接AD.取格點E,F,連接EF交AD于點P.連接BP,取格點K,連接CK交BP于點Q.點P,Q即為所求.
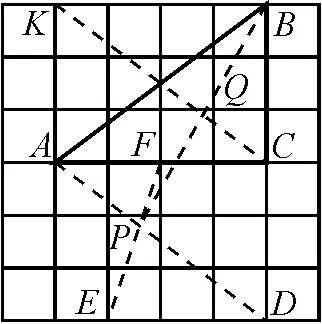
圖12
涉及知識點:①最值,即隱圓問題;②三角形中位線性質;③網格作圖基本動作——比例分線段.
4 作圖思路總結
結合以上六個例題,匯總常見作圖的思路:
(1)通過圓周角90°確定直徑;
(2)通過兩直徑確定圓心;
(3)通過等弧所對圓周角相等確定角平分線;
(4)通過直徑確定圓周角90°(即兩直線垂直關系);
(5)通過隱圓確定動線段的最短、最長線段.
5 結束語
網格作圖問題承載著幾何直觀能力、邏輯推理與合情推理能力、運算能力、應用意識、創新意識等學科核心素養的落地體現,同時,蘊涵著轉化、化歸、數形結合、數學建模等數學思想,是中考命題的熱點之一.以往網格作圖問題通常依托于全等、相似、線與線的相對位置、三角形或四邊形的基本性質,讓學生利用網格作垂直、平行,構造相似與全等,將線段n等分[1].而今試題增加了圓這一背景后,增加了知識的綜合性,使試題更靈活,借助圓心、半徑、直徑、圓心角、圓周角、切線等的基本性質,作圖更便捷,思維更廣闊,既能考查學生綜合解決問題的能力,又能呈現出更加美觀的作圖效果.利用網格與圓相關性質的結合還可以解決更多幾何變換中旋轉、翻折等典型問題.

