基于外測觀測的再入飛行轉彎方向辨識方法

淡 鵬， 王 丹, 李恒年

(1. 宇航動力學國家重點實驗室， 陜西西安 710043； 2. 西安衛星測控中心， 陜西西安 710043)

0 引 言

航天器再入返回[1-3]地球過程中，為使其著陸于特定的位置或區域，再入飛行時需要不斷調整飛行方向，使其按照事先設計好的制導方法向目標點或目標區域飛行。在一些機動能力較強的航天器再入飛行中，有時需要對其飛行過程的轉彎方向進行實時辨識，以便更好地判斷及預測其實際的飛行路徑情況(有時飛行器因為離軌制動控制差異、大氣環境變化影響等而未能按照事先設定的路徑飛行)。

由于黑障[4-6]的影響，航天器再入飛行過程部分時段會出現遙測下傳中斷的現象，此時就無法從遙測數據中獲取有效的飛行姿態及氣動參數信息，故而辨識不出其轉彎方向。這種情況下，來自于地面外測[1]設備的觀測數據就成為黑障中或姿態不穩定過程中航天器飛行狀態估計的主要可依賴數據。另外在一些非合作目標的再入觀測中，目前也主要依賴雷達[7]等外測測量數據。

因缺乏姿態信息，航天器再入飛行過程中僅外測觀測下的轉彎方向辨識只能從外測數據中的測距、方位角、仰角、測速(測距變化率)等觀測量上入手，而這幾類數據運動特征不明顯，不能直接轉換出速度信息，從而給轉彎方向的辨識帶來一定困難。

關于再入飛行轉彎方向的實時辨識問題，經查詢很難找到類似的解決案例或文獻作為參考。為此，針對部分航天器再入返回工程實施過程中遇到的這一實際問題，在對再入飛行過程受力分析的基礎上給出了一種轉彎方向的實時在線辨識方法。

1 轉彎方向辨識方法

1.1 再入過程受力情況

航天器再入段飛行過程主要受到地球引力、大氣阻力、氣動升力的作用。而其他攝動力的量級較小，在再入飛行過程中可忽略不計[8]。這幾個主要的作用力如圖1所示。

圖1 再入過程主要受力示意圖

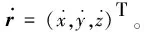
僅考慮J2項時，地球引力加速度在地心矢徑r和地球自轉軸矢量we上的分量gr,gw分別為

(1)

式中：J2=1.082 63×10-3為二階帶諧項系數；μ=3.986 005×1014m3/s2為地球引力常數；Re為地球赤道半徑。

設ρ為大氣密度(kg/m3)，v是航天器相對大氣的速度，其矢量模為v(m/s)，Sref為飛行器參考面積(m2)，m為飛行器質量(kg)，CL和CD為升力系數和阻力系數(無量綱)。

大氣阻力在地球固連系(與J2000慣性系可相互轉換)下的加速度為

(2)

氣動升力在地球固連系下的加速度為

(3)

式中，C0為航天器所受總升力再入縱平面的側向分量在地固系下的單位矢量，L0為航天器總升力再入縱平面內分量在地固系下的單位矢量,γ為傾側角。

從這幾個主要作用力的代數式可見，再入飛行過程中軌道面的法線方向主要受到氣動阻力法向分量、氣動升力法向分量、地球非球形攝動力法向分量的影響。而實際計算中發現，地球非球形攝動力的法線分量相對其他幾個量明顯較小[8]。

由此，航天器實際再入飛行過程中，通過對姿態角的控制，特別是在其發生滾轉以后，升力在當地鉛垂面和水平面上的分量會發生改變，從而使航天器具有了一定的縱向機動和側向機動能力，進而可實現方向轉彎。

也就是說，通過實時計算當前軌道平面法向的加速度或速度變化即可對滾轉過程發生的轉彎方向進行辨識。

基于以上分析，本文對滾轉方向辨識的思路是：當只有外測測量數據時，先通過濾波算法使用外測觀測量計算出飛行彈道的速度矢量，然后計算當前速度與前一點的速度差(速度增量)在前一點速度法線方向的分量；進而通過對一系列時間點處的法線方向速度分量的滑窗統計來獲取對航天器轉彎方向的判斷。

1.2 再入飛行外彈道計算模型

再入飛行過程外彈道測量數據(主要為測距、測速、測角)無法直接計算出速度參數，除幾何方法、差分方法外，可采用濾波算法來實現飛行彈道中速度參數的估計。考慮到再入飛行時受力情況較為復雜，無姿態及其他氣動參數遙測信息時(僅外測觀測下)，較難進行飛行狀態的動力學建模[1]，故此處考慮采用非動力學建模算法進行濾波計算。

在非動力學建模方法中，“當前”統計模型[9-11]是機動目標建模的一種較常用算法。“當前”統計模型把機動目標加速度的一步預測看作是“當前”機動加速度，并采用該加速度作為修正瑞利分布的均值來實現目標自適應跟蹤。由于采用非零均值的機動加速度和相應機動加速度方差的自適應調整，因此具有較好的機動目標跟蹤能力。

無跡卡爾曼濾波[12-14](UKF)是由牛津大學機器人技術研究所Julier和Uhlman等人于1995年提出的，后來被推廣到非線性動力學系統參數估計中。UKF算法的核心是UT變換，它選擇2n+1個Sigma采樣點來逼近樣本非線性變換參量的矩，能達到真實值的三階精度。同時UKF算法不需要求導計算Jacobian矩陣，不需要清楚地了解非線性函數的具體形式，便于進行模塊化開發，因而在工程中有較大的應用價值。

基于以上考慮，本文將采用當前統計模型及UKF濾波算法來實現僅外測觀測下飛行彈道中速度參數的估計。

“當前”統計模型下的狀態外推模型為

X(k+1|k)=Φ(k+1|k)X(k|k)+

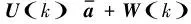
(4)

因x、y、z各方向相互正交，則有Φ=diag{Φx,Φy,Φz},U=diag{Ux,Uy,Uz}。

狀態噪聲協方差陣

Q=E{W(k)·WT(k)}=diag{Qx,Qy,Qz}

(5)

對x、y、z各方向，有

(6)

x、y、z三個方向上噪聲協方差陣Qi(i=x,y,z)的計算公式為

(7)

式中，

(8)

(9)

這樣就建立了一種外測觀測下的基于當前統計模型的UKF濾波再入飛行彈道估計算法。

1.3 濾波觀測模型建立

由于外彈道測量數據中各類觀測數據的質量不一，一般情況下測距數據質量較高、而測角數據質量較差，為此，濾波時將觀測模型建立在測站地平坐標系下，以便充分利用不同精度的觀測量。則觀測方程為

(10)

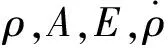
1.4 濾波初始化方法

濾波計算時的一個重要內容是起步初值的計算，考慮到再入過程中外測跟蹤數據建立在測站地平坐標系下，無法直接轉換為J2000.0坐標系的位置速度，但可以由測距和測角值計算出位置矢量，因此可通過多個點的曲線擬合完成起步計算。

取多個連續的觀測點，設第j個點處測量值時間、測距、方位角、仰角分別為tj，ρj,Aj,Ej。由測站坐標可計算出測站東北天坐標系到J2000.0地心慣性系的轉換矩陣為Mtj，則可計算出各點在測站東北天坐標系下的位置矢量為

Rdj=[ρjcosEjsinAjρjcosEjcosAjρjsinEj]

j=0,1,2,…

(11)

則各點在J2000.0坐標系下的位置矢量為

(12)

進而對該位置數列使用最小二乘曲線擬合后求導的方法可計算出速度初值。

狀態方程中加速度等其他參數的起步初值可設置為0。這樣就得到了濾波的起步初值。

1.5 單點轉彎方向辨識

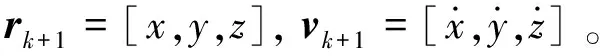
則前一時刻軌道面的法線方向單位矢量為

Nk=rk×vk/‖rk‖/‖vk‖

(13)

當前時刻與前一時刻的速度差為

(14)

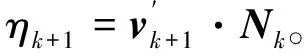
給定一個小值(定義為σ，σ≥0)，用于判斷轉彎方向是否為0。

則可定義轉彎方向的辨別函數為

(15)

當F取值為1時，表示左轉(順著飛行速度方向觀察時)；取值-1時，表示右轉；取值為0時，表示未轉彎(或值太小無法辨識)。

這樣就得到了當前時刻的轉彎方向的辨識值。

此方法是利用速度增量在軌道面法向上的分量進行轉彎方向的辨識計算，考慮到轉彎時軌道面法線方向上的速度增量將直接在下一時刻的速度矢量上體現出來，因而上述計算過程也可直接簡化為計算k+1時刻的速度vk+1在k時刻軌道面法線方向Nk上的投影大小的判斷。即用λk+1=vk+1·Nk代替ηk+1，并運用該判別函數進行轉彎方向的判斷。

1.6 多點滑窗統計

由于濾波計算時存在“震蕩”收斂問題，以及某點數據質量較差[1]時可能影響單點判斷結果的準確性。因而僅僅使用上面的單點轉彎方向辨識方法可能會出現錯判的情況。為此，實際工程使用中，還不能直接使用上面的單點判別結果，而需要進行多點數據的綜合判斷。

為此，在飛行過程的實時監視計算中，可采用多點滑窗統計的方法來進行轉彎方向的辨識。

設固定使用當前時刻及其之前n-1個時間點上的單點辨別結果進行統計計算，這n個時間點上的辨識結果分別為f1,f2,…,fn，則可統計出值為1的點數為n1，值為-1的點數為n-1。設綜合判斷閾值為ε(0.5<ε≤1，值越大越可靠，但判斷不出的可能性也將變大)，當n1/n>ε時可認為發生左向轉彎，當n-1/n>ε時認為發生右向轉彎，否則認為無法辨識出轉彎方向(或未發生轉彎)。

2 計算及分析

為了驗證算法的正確性，采用某航天器再入返回過程的理論彈道數據進行仿真計算(該航天器再入飛行中的側滑角為小量，可忽略)，按多站接力方式生成仿真數據，并對各站的測距、測角、測速分別設置50 m、0.02°、0.05 m/s的隨機誤差。

使用本文算法實時計算轉彎方向，并與其在軌道系下的理論滾動姿態角給出的轉彎方向進行對比。

對軌道系下的滾動姿態角(記為φ)，給定一個比較閾值σ2(σ2>0，此算例中取為0.01°)，結合滾動角的定義，當φ>σ2時，認為右轉；當φ<-σ2時，認為左轉。

為了對比明顯，將兩種方法表示的左轉及右轉值進行區分。

方法1為采用本文濾波及多點滑窗算法的判別結果，左轉辨識結果取值為1，右轉辨識結果取值為-1；方法2為滾動姿態角判別出的轉彎方向，左轉取值為0.9，右轉取值為-0.9；無法判斷時兩種方法均取值為0。

使用這兩種方法計算的轉彎方向值對比如圖2所示。

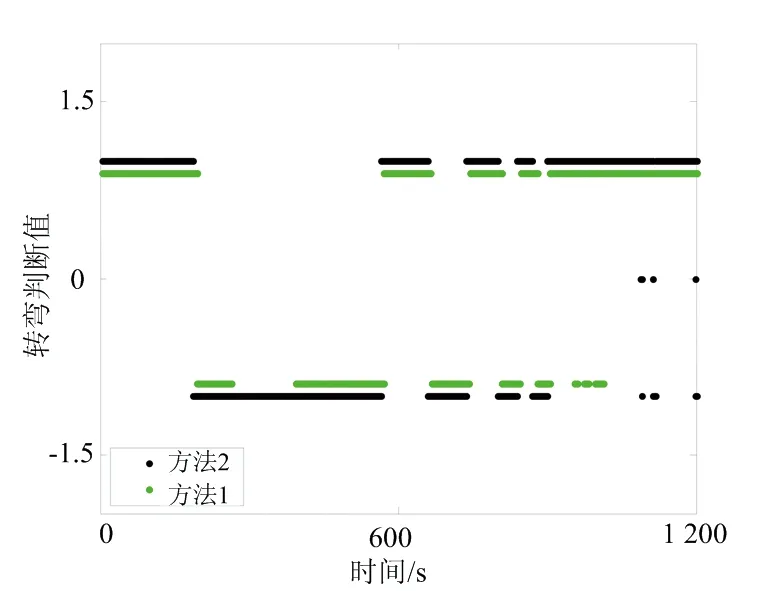
圖2 兩種方法轉彎方向對比

需說明的是，因為所仿真的外測測量量有些弧段沒有觀測值(設備跟蹤不上)，故圖2中部分時段只有理論姿態角的計算值，而無外測濾波計算值的判別結果(方法1)。

從圖中可見，兩種方法判別的轉彎方向基本上是一致的，這說明本文算法是可行的。由于濾波震蕩問題使其部分點存在誤判的情況，但大多數點均判別正確。另外，濾波輸出的判斷結果存在稍微滯后的現象(1～5 s，各處存在差異)。但總體上來看，本文算法是有效的，對轉彎方向判別的正確率較高。

造成濾波判斷稍滯后的原因在于：1)濾波計算結果相對于測量數據時標的滯后；2)多點滑窗統計造成的統計滯后。第一種因素改善稍顯困難，需從提高數據的質量，以及尋找新的濾波算法模型上下功夫；第二種可從減少滑窗時長，或增加每秒時長內數據采樣個數等方面入手，在采樣頻率不變的情況下，減少時長可能會使得誤判的幾率放大，所以需要權衡處理。因為本文的滑窗算法是時間上逐點滑動的，所以算法本身不會帶來處理延遲。

需要說明的是，本文方法在轉彎方向辨識時未考慮側滑角的影響(當側滑角很小時)，這樣才可直接與滾動角判斷出的轉彎方向比較。否則，在實際計算和比較過程中還需要考慮側滑角的影響。

3 結束語

針對僅外測觀測下的再入飛行過程中轉彎方向的實時辨識問題，提出了一種基于UKF濾波及速度增量(或速度)法向分解的解決方法。從仿真計算結果來看，本文算法是可行的。

在使用該方法時需要注意的是：對于飛行中轉彎方向的實時辨識所用的判斷閾值不應太小，否則可能將極小作用力的加速度考慮進去。也就是說，只有法線分量絕對值大于某一值后，才能認為轉彎方向可判斷(可通過事先對理論飛行彈道分析的方法給定閾值)。

考慮到一些航天器外形比較復雜，致使返回過程的受力飛行分析更加困難，下一步將在考慮側滑角的轉彎方向辨識方面進行研究。