基于電磁計算的非平整表層回波抑制方法

黃雅文， 何志華， 劉 濤， 陳 誠， 余安喜， 黃春琳

(1. 中國人民解放軍96717部隊， 浙江金華 321000； 2. 國防科技大學電子科學學院， 湖南長沙 410073)

0 引 言

全息穿透成像雷達(Holographic Subsurface Imaging Radar，HSIR)利用電磁波的穿透特性和微波全息成像工作原理，通過二維合成孔徑掃描獲取回波數據，利用相位信息進行相干成像，以二維圖像呈現介質內埋藏目標或者材料缺陷的投影圖像，具有高空間分辨率、高穿透能力、快速、無損等優點，可廣泛應用于無損檢測、建筑、反恐、安檢等領域[1-3]。

全息穿透成像雷達向介質發射電磁波時，除目標外，不同來源的反射波也被接收，如天線間的直接耦合波、空氣-介質交界面的表層回波、介質內腔隙顆粒等雜散物體造成的散射波[4]等。對于非平整表面介質，尤其對于高程差可與發射波長相比擬的介質而言，表層回波隨介質表面高程變化而變化，沒有一致的規律，難以校準和去除，且介質表面相較于介質內埋藏目標距離天線更近，電磁波傳輸過程中損耗更小，因此一般來說非平整表層回波遠大于埋藏目標回波，這使得目標回波淹沒于表層回波等雜波之中[5-6]。

為抑制非平整表面效應對穿透雷達成像產生的影響，現有研究采取了多種物理方式。典型的有在估算介質介電常數的基礎上，獲得與此介電常數相似的柔性填充物，以填平非平整面[7-8]，然而此種方法難以獲取合適的填充物；另一種方法是設計共形天線陣列或天線的掃描面與介質面共形，這對于形狀規則的介質可以做到，比如圓柱、球形等，這方面的應用可以追溯到對乳腺癌的檢測—半球形天線陣列對乳房探測成像[9]，以及圓柱掃描系統安檢設備對人體衣物下隱藏武器的探測等[10-12]，這類方法只能應用于特定場景。基于介質的表層高程及其屬性以估計表層回波并加以消除是一類更通用的方法：文獻[13]提出對于特定形狀的介質，利用其形成的回波特征來識別并消除表層回波，實測實驗驗證該方法對特定介質有效；文獻[14]提出在獲得非平整表面高程數據后，基于幾何光學法對表層回波擬合，通過背景對消抑制實測數據中的表層回波。文獻[14]的方法能夠抑制表層回波，然而因其擬合精度不高的問題，雜波抑制過后，仍有過量雜波影響成像質量。

本文提出了一種基于電磁計算的非平整表層回波抑制方法，該方法依據雷達散射特性加性模型，在已知非平整表面高程信息條件下，利用電磁計算工具擬合表層回波，并與實測數據相減消除表層回波，得到近似目標回波，從而達到抑制表層回波的目的。

1 非平整表層回波抑制方法原理

全息穿透成像雷達掃描示意圖如圖1所示，對該掃描空間建立三維直角坐標系，其中雷達掃描面平行于XY平面，收發天線以固定掃描間隔依次沿X向Y向二維掃描，掃描面與介質之間為空氣層。電磁波離開發射天線后，在介質表面處發生后向散射與折射。假設介質的介電參數處處均勻，則電磁波在介質內傳輸時，除遇目標外，不發生反射。此外，由于收發天線無法完全隔離，部分電磁波經空間直達接收天線，形成直接耦合波。因此，雷達在掃描位置(x,y)處接收到的回波能量分別是收發天線之間的直接耦合波So(x,y)、介質表面反射回波Ss(x,y)以及目標回波St(x,y)三者的矢量疊加[4]：

S(x,y)=Ss(x,y)+St(x,y)+So(x,y)

(1)

對于直耦波，因收發天線相對空間位置保持固定，其值不隨掃描位置變化，可作為直流分量去除，不影響對目標的成像。此時回波可簡化為

S′(x,y)=Ss(x,y)+St(x,y)

(2)

式中，介質表面反射波是關于空間掃描位置的變量，當介質表層不平整時，表層回波隨掃描位置變化，使得表層回波與目標回波疊加后，難以直接分離。考慮到介質表層靠近天線，表層回波幅度往往強于目標回波，使得目標回波雜糅于雜波之中，甚至淹沒于雜波之中，因此必須將表層回波抑制才能有效成像。

圖1 全息穿透成像雷達掃描示意圖

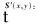
(3)

再對S′t(x,y)進行成像處理，即可實現對表層不平整介質內隱藏目標的成像。

在擬合回波Cs(x,y)時，還需附加幅度和相位校準因子，以補償計算模型與實際雷達系統的誤差。總結而言，可得算法流程圖如圖2所示。

圖2 算法流程圖

2 表層雜波電磁計算方法

用電磁數值計算方法對表層回波進行擬合時，應根據發射頻率、天線特性、介質大小等選擇不同數值計算方法，例如時域法、頻域法以及高頻法。同時，電磁計算工具可對天線精確建模，相比于幾何光學法[14]提高了仿真精度。不僅如此，可對回波的最低接收能量進行設置，從而提高擬合精度。

利用電磁計算工具擬合雷達回波的基本步驟為：

1) 結構建模，主要包括：

① 對已知高程數據的非平整表面介質三維建模，如圖3(a)所示；

② 量測實際天線尺寸，對收發天線三維建模并設置端口，如圖3(b)所示。

2) 設置激勵信號模擬雷達發射信號。

3) 計算并獲取回波數據。

(a) 非平整表面介質

(b) 收發天線圖3 電磁建模示例

獲取回波數據前，雷達系統的參數：天線類型、天線三維數據、激勵源、天線距介質表面的高度、掃描點的位置等需針對具體的雷達系統進行設置。同時，介質的表面高程及介電屬性也需與實際盡可能一致。

3 表層回波自適應對消處理

電磁數值計算與實際探測場景設置不可避免地存在一定誤差，如介質介電參數、介質表面高程、背景電磁環境，以及雷達系統的建模誤差。因此，擬合回波與實測回波在幅度與相位上存在差異。造成差異的原因包括但不限于以上因素難以精確補償，但對于給定的探測場景，表現為固定差異的部分，可通過相位與幅度校準去除。

3.1 幅度校準

理想條件下，擬合回波與實測無目標背景回波對應掃描點的幅度之比應相同。為應對上述因素造成的干擾，且為了避免隨機干擾帶來的誤差，對實測回波處理，將疑似目標區域去除得到背景回波，對其幅度累加求得與擬合回波相差倍數，用該倍數對擬合回波校準，可用以下公式表達：

(4)

(5)

式中S′p(x,y)為實測回波中除去疑似目標區域的部分，相應的Cs(x,y)中該部分區域也應去除得到Csp(x,y)。當目標回波完全淹沒于雜波中時，可認為S′(x,y)≈S′p(x,y)，Csp(x,y)≈Cs(x,y)。

3.2 相位校準

幅度校準后，采用以下準則估計相位誤差，計算準則[14]為

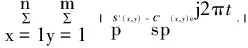
0≤t≤1

(6)

式中C′sp(x,y)為C′s(x,y)中去除疑似目標區域的背景回波，F為代價函數。當代價函數F在0≤t≤1范圍內值最小時，此時的t=t0值即為所求，即對擬合回波的相位偏移2πt0值，得到C″s(x,y)=C′s(x,y)ej2πt，可對擬合回波實現校準。

4 實驗驗證

4.1 場景設置

(a) 方塊尖頂介質

(b) 雙余弦介質

(c) 矢量網絡分析儀

(d) 天線及XY掃描平臺

(e) 方塊尖頂介質計算模型

(f) 雙余弦介質計算模型圖4 介質及實驗場景

實驗的介質材料為圖4(a)、(b)所示的兩塊非平整表面介質，其中方塊尖頂介質為40 cm×40 cm×3.5 cm ABS(Acrylonitrile Butadiene Styrene)塑料(3.5 cm為最大厚度)，最大高程差1.5 cm，雙余弦介質為40 cm×40 cm×3.3 cm ABS塑料(3.3 cm為最大厚度)，最大高程差1.3 cm，分別模擬非平滑突變曲面和平滑漸變曲面。如圖4(d)所示實測場景，介質在XY掃描平臺控制下沿固定距離移動，收發天線連接矢量網絡分析儀(圖4(c))并固定在介質上方，發射波為7 GHz正弦連續波，掃描方式為停-走-停，掃描范圍18 cm×18 cm，掃描間隔6 mm。采用有限積分法(Finite Integration Technique，簡稱FIT)數值計算方法計算擬合回波，該方法將待求空間網格化，每個網格具有不同的電磁屬性，將麥克斯韋積分方程離散化，可采用計算機進行求解。利用電磁計算工具擬合回波的計算模型如圖4(e)、(f)所示。

實驗中以垂直交叉布置的銅條為目標，如圖5所示，銅條緊貼于介質下表面，長10 cm，寬1 cm。為檢查天線極化對成像的影響，以及非平整表面對目標回波傳播路徑影響下的算法性能，圖5(a)所示銅條與水平方向成45°角，圖5(b)所示銅條置于水平方向。實驗中，方塊尖頂介質與雙余弦介質均使用這兩組目標。

(a) 45°角

(b) 正十圖5 目標及其與掃描視場相對位置

4.2 幅相校準及數據處理結果

圖6(a)、(b)為兩介質電磁數值計算的擬合回波，圖6(c)、(d)為無目標的實測背景回波。對比可知，兩者所反映的介質表層對電磁波的散射趨勢相似。

結合公式(4)、(5)、(6)，幅相校準步驟表示如下：

1) 對實測回波成像，以確定疑似目標區域，若無法確定，即目標回波淹沒于雜波中時，跳至步驟3)；

(a) 方塊尖頂介質擬合回波

(b) 雙余弦介質擬合回波

(c) 方塊尖頂介質實測背景回波

(d) 雙余弦介質實測背景回波圖6 擬合回波與實測背景回波

2) 去除實測回波和擬合回波中疑似目標區域；

3) 求得實測回波、擬合回波各點的幅度并累加求和；

4) 求得擬合回波、實測回波幅度累加和之比k；

5) 原始擬合回波各點數據除以k，得到C′s(x,y)。

幅度校準后，進行相位校準：

1) 去除實測回波、擬合回波C′s(x,y)中疑似目標區域；

2) 對擬合回波各點數據附加一固定相位，該相位在[0,2π]范圍內等間隔獲取，即二維數據增加了一維Z向，得到一三維擬合回波；

3) 實測回波與每一附加固定相位的擬合回波相減，得到一新的三維數據；

4) 遍歷該三維數據中的Z向，對每一Z向二維數據幅度累加求和，得到一維向量F；

5) 求向量F中的最小值；

6) 當F取最小時，獲取此時擬合回波附加的相位φ；

7) 對擬合回波C′s(x,y)附加相位φ。

圖7所示為方塊尖頂介質與45°角銅箔的處理結果。其中，圖7(a)為原始回波，圖7(b)為原始回波成像，圖7(c)為原始回波經所提算法抑制雜波的成像，圖7(d)為原始回波減背景回波的成像，其中背景回波為實驗室條件下得到的數據，在現實應用中該值無法獲得，然而此時雜波抑制最為徹底，成像效果最好，本文用做圖7(c)成像的對照組。

由圖7可知，原始回波成像(圖7(b))的表層回波相較于圖7(c)、(d)較為嚴重，雜波形成偽像，且目標像不完整，無法辨別目標的形狀大小。抑制雜波后的成像(圖7(c))，雜波被有效抑制，其強度遠小于目標回波，且目標像得以完整呈現。圖7(c)與圖7(d)對照，圖7(c)的雜波稍強于圖7(d)。對圖7(c)目標長度測算為100 mm(見圖中白色矩形框)，與目標實物的大小、形狀一致。

(a) 原始回波 (b) 原始回波成像 (c) 抑制雜波后成像 (d) 減背景回波成像圖7 方塊尖頂介質—45°角銅箔實測數據及處理

圖8除具有圖7的實驗結論外，可以看到目標像水平方向與垂直方向銅箔的長度不一致，這與實物不同，分析知與天線的極化方式有關，本實驗使用角錐喇叭天線，為線極化，會致使某一掃描方向的接收回波相對弱小，使得目標像形狀與實際形狀存在差異。

采用雙余弦介質進行實驗，如圖9、圖10所示。由圖9可知，原始回波成像圖中， 目標本身回波較強，因而可直接成像，但受介質表層雜波的影響，直接成像結果中目標嚴重失真。抑制雜波后(圖9(c))，目標像的形狀大小均得以呈現。圖10結果與圖9結果相似，不再贅述。

(a) 原始回波 (b) 原始回波成像 (c) 抑制雜波后成像 (d) 減背景回波成像圖8 方塊尖頂介質—正十銅箔實測數據及處理

(a) 原始回波 (b) 原始回波成像 (c) 抑制雜波后成像 (d) 減背景回波成像圖9 雙余弦介質—45°角銅箔實測數據及處理

若無幅相校準，實測回波與擬合回波直接對消，四組實驗的成像如圖11所示。分別與圖7～10(c)幅相校準后成像圖對照，可見圖11中雜波較強，目標像被掩埋。證明了幅相校準有效地抑制了擬合回波與實測回波幅相的差異性。

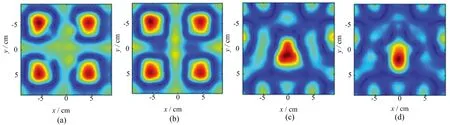
圖11 四組實驗實測回波與擬合回波直接對消成像

4.3 處理結果評估

為了評估圖7～10中各成像圖(原始回波成像，抑制雜波后成像，減背景回波成像)的成像質量，采用信雜比評估成像質量提高的程度。為提高數據間比較的有效性，計算信雜比時，同一原始回波的三幅成像圖中，選擇同一區域作為目標區。計算結果如表1所示。

表1 成像信雜比對照表 dB

觀察表1中數據可知，信雜比反映的圖像質量改善情況與視覺觀察一致。應用算法抑制雜波后的成像相較直接成像的信雜比提高明顯，尤其方塊尖頂介質表層回波較強的情況，所提算法也能很好將其抑制。兩介質抑制雜波后的成像圖與減背景回波成像圖的信雜比相比仍有一定差距，但抑制雜波后的成像已能夠對目標檢測、判別，對此類存在弱雜波的成像，可通過非線性增益控制算法[15]抑制，以獲得高質量成像。

5 結束語

非平整表面介質產生的表層回波是制約全息穿透成像雷達發展的重要因素。本文為抑制介質表面高程差可與波長相比擬的表層回波，提出了一種基于電磁計算的表層回波擬合方法，該方法利用電磁計算工具對已知介質表面高程的表層回波進行擬合，并對擬合數據的幅度、相位自適應校準，之后與實測數據對消，從而抑制其影響。實驗結果表明，擬合的表層回波與實測中的表層回波匹配良好，實現了對表層回波的有效擬合，進而抑制了表層回波對成像的影響，改善了成像質量。