SUP-ADDITIVE METRIC PRESSURE OF DIFFEOMORPHISMS*
Wenda ZHANG(張文達(dá))
College of Mathematics and Statistics,Chongqing Jiaotong University,Chongqing 4000714,China E-mail: wendazhang951@aligyun.com
Zhiqiang LI (李智強(qiáng))*
College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China E-mail : zqli@cqu.edu.cn


In terms of the category of differentiable dynamics, dynamical invariants such as entropy and pressure are developed for diffeomorphisms on closed Riemannian manifolds, especially for C1-smooth partially hyperbolic diffeomorphisms. A fundamental result is due to Hu, Hua,and Wu ([8]), who introduced the unstable topological and metric entropy, obtained the corresponding Shannon-McMillan-Breiman theorem, and established the corresponding variational principle. In[14],Tian and Wu generalized the above result with the additional consideration of an arbitrary subset(not necessarily compact or invariant). In[9],Hu,Wu,and Zhu investigated the unstable topological pressure for additive potentials,and obtained a variational principle. In[17] and [18], we introduced unstable topological pressure and metric pressure for sub-additive potentials, and set up a variational principle between unstable topological pressure, measure theoretic entropy, and the corresponding Lyapunov exponent.
In this paper, still in the setting of C1-smooth partially hyperbolic diffeomorphisms, we extend the theory of pressure to the context of sup-additive potentials, whose counterpart for purely topological dynamics is in [4]. We give several definitions of unstable pressure, in terms of Bowen’s picture and the capacity picture, together with consideration of an arbitrary subset in a topological context. Note that the way of defining pressure for sup-additive potentials is slightly different from that for sub-additive potentials in[18], which enables us to get rid of the tempered variation assumption on the potentials; see [19, 20]. We show that all such unstable metric pressure regarding a given ergodic measure equals the corresponding unstable measure theoretic entropy plus the Lyapunov exponent of the potentials. Our proofs are influenced by the purely topological counterpart in [4], but we also need to work on unstable manifolds,which causes new problems and difficulties; in particular, for any Borel probability measure μon a closed Riemannian manifold M and any measurable partition η, we have to consider the measure disintegration of μ over η with respect to unstable manifolds.
Theorem 1.1 Suppose that M is a finite dimensional, smooth, connected, and compact Riemannian manifold without boundary, and that f :M →M is a C1-smooth partially hyperbolic diffeomorphism. Let there be given a sequence of sup-additive potentials Φ={φn}nof f on M. Then, for any ergodic measure μ of f on M, one has

(All terms involved are defined in Section 2; see Definition 2.3,Remark 2.4,Definitions 2.5,2.8,and 2.10.)
The rest of the paper is organized as follows: in Section 2, we set up notation and give definitions of unstable (metric) pressure. In Section 3, we prove the main result Theorem 1.1. To be precise, we first establish three lemmas which connect unstable pressure for supadditive potentials to the unstable pressure of additive potentials, and with their help we give the necessary estimates of unstable metric pressures, then we proceed to complete the proof of Theorem 1.1.
2 Notation and Definitions
Throughout the paper, we focus on the dynamical system (M,f), where M is a finite dimensional, smooth, connected, and compact Riemannian manifold without boundary, and f : M →M is a C1-smooth partially hyperbolic diffeomorphism. We say that f is partially hyperbolic if there exists a nontrivial Df-invariant splitting T M = Es⊕Ec⊕Euof the tangent bundle into stable, central, and unstable distributions, such that all unit vectors vσ∈Eσx(σ =s,c,u) with x ∈M satisfy

for some suitable Riemannian metric on M. The stable distribution Esand unstable distribution Euare integrable to the stable and unstable foliations Wsand Wu, respectively,such that T Ws=Esand T Wu=Eu.
We denote by Mf(M) the set of invariant Borel probability measures of f on M, and by Mef(M) the subset of ergodic ones.
First we recall some basic facts about unstable entropy (see [8]).
Take an ?0>0 small. Let P = P?0denote the set of finite Borel partitions α of M whose elements have diameters smaller than or equal to ?0; that is, diam α:=sup{diam A:A ∈α}≤?0. For any partition ξ of M and any x ∈M, we denote by ξ(x) the element of ξ containing x. For each β ∈P we can define a finer partition η such that η(x) = β(x)∩Wuloc(x) for each x ∈M, where Wuloc(x) denotes the local unstable manifold at x whose size is greater than the diameter ?0of β. Since Wuis a continuous foliation, η is a measurable partition with respect to any Borel probability measure on M.
Let Pudenote the set of partitions η obtained in this way and subordinate to unstable manifolds. Here a partition η of M is said to be subordinate to unstable manifolds of f with respect to a measureμif forμ-almost every x,η(x)?Wu(x)and contains an open neighborhood of x in Wu(x). It is clear that if α ∈P satisfies μ(?α) = 0, where ?α := ∪A∈α?A, then the corresponding η given by η(x)=α(x)∩Wuloc(x)is a partition subordinate to unstable manifolds of f.

This is also called the measure disintegration of ν over η. A classical result of Rokhlin(cf.[12])says that if η is a measurable partition, then there exists a system of conditional measures with respect to η. This is essentially unique in the sense that two such systems coincide with respect to a set of points with a full ν-measure. For measurable partitions α and η, let
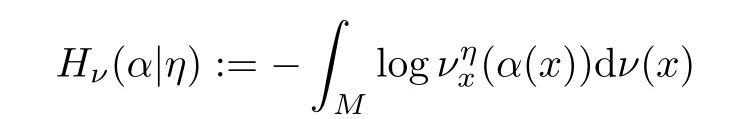
denote the conditional entropy of α for given η with respect to ν.

Remark 2.2 In[8],the authors proved that hμ(f|η)is independent of η ∈Pu. Moreover,for any ergodic measure μ, any α ∈P?(?small enough), and any η ∈Pu, one has huμ(f) =hμ(f|η)=hμ(f,α|η) (see Lemma 2.8 and Theorem A there). We shall use this fact frequently throughout the rest of the paper.
Definition 2.3 Let Φ = {φn}nbe a sequence of continuous functions on M. We call Φ a sup-additive sequence of potentials of f if

(If the inequality reverses, then Φ is called a sub-additive sequence of potentials of f on M.)
Remark 2.4 Given a sequence of sup-additive potentials Φ = {φn}nof f on M, and considering Φ'={-φn}n, we have a sub-additive, that is,



Remark 2.11 1)In all of the definitions above,when we make summations at the beginning, we directly take the evaluation of a potential function on a point in a spanning set,rather than taking the supreme over Bowen balls;this is slightly different from the case of sub-additive potentials,which enables us to get rid of the tempered variation restriction on potentials. Moreover, we should point out that for additive potentials, the corresponding pressures, defined in two ways (regarded as either sub-additive or sup-additive potentials), actually coincide.
2)The definitions above are inspired by the Carath′eodory dimension theory,and they enjoy the following properties that are similar to the case of dimension theory:

Proof i) and ii) follow directly from the definitions, and iii) follows from the standard Carath′eodory dimension characteristic;this can be proved by an argument quite similar to the proof of Theorem 1.4 (a) in [2]. Finally, iv) follows from iii). □
3 A Formula of Unstable Metric Pressure
Lemma 3.1 Let Φ = {φn}nbe a sequence of sup-additive potentials of f. For any positive integer k, there is a constant C satisfying the following: for any ρ>0, there exists an?0>0 such that for any 0 <?<?0, one has
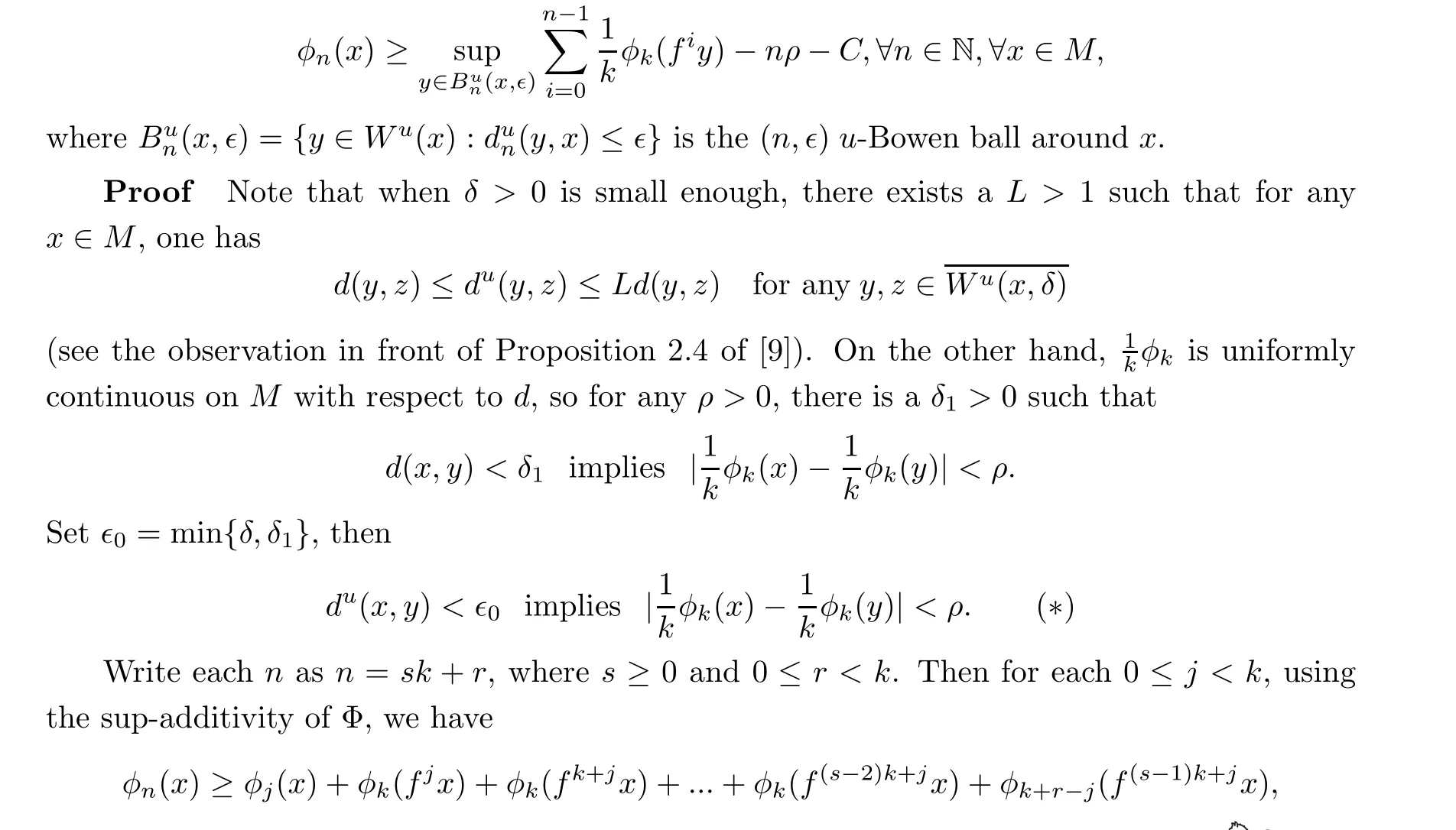


Remark 3.7 This proposition and its proof indicate that,for a subset A whoseμ-measure is close to one, we can find another subset B whose μ-measure is also close to one such that,for any x ∈B, one has that μηx(A) is large enough up to one. The parameters c1,c2above are not essential, and are only for technical applications later. Such constructions have appeared before in [6].
Theorem 3.8 For any μ ∈Mef(M) and any sequence of sup-additive potentials Φ ={φn}nof f, one has
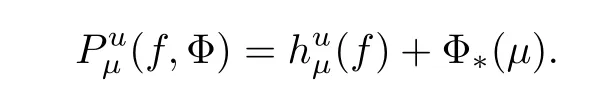



Furthermore, the balls {Bun(y,?/2)|y ∈E} are mutually disjoint, and by (3.1), the cardinality of E is less than or equal to en(hμ(f|η)+ρ).
Therefore,

which completes the proof. □
Remark 3.11 From the proof of Theorem 1.1, one can see that the case Φ?(μ)=+∞is implicitly verified.
 Acta Mathematica Scientia(English Series)2022年2期
Acta Mathematica Scientia(English Series)2022年2期
- Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
