分類討論思想視域下高中數學解題研究
崔 堅
(山東省德州市臨邑第一中學 251500)
高中數學解題中運用分類討論的思想,不僅能夠使數學題目得以輕松解決,而且還能使學生形成相應的發散思維.高中階段的數學與其他時期不同,通常具有較強的抽象性,不易被學生所理解.而分類討論作為數學解題中的一種重要思想,其在高中數學的許多題目解決中都得到廣泛運用,如概率、函數、數列等,其不僅可以使學生在解題時,具有清晰的思路,而且還能將抽象思維轉變為形象思維,以確保相關數學題更好的完成.因此,想要使高中數學的解題有效性得到顯著提高,就需深化分類討論的探究,以促使復雜、抽象的數學題解答更加簡單,并使學生形成良好思維習慣的同時,實現數學成績的提高.
1 分類討論思想及其應用價值與原則
1.1 分類討論思想概述
基于高中階段數學學科具備的特點,學生在對數學知識進行學習時,通常會遇到各種難題,且學生在解答數學題的時候,其中還包含著無限的可能,這就造成學生無法通過常規的形式進行數學試題解答.面對該數學問題,學生需注重具體問題具體分析,依據數學題所限定的范圍,對其實施正確劃分,將其分為一個個的小區域開展分析與運算,以促使學生的解題能力得到有效提高,該過程中運用到的數學思想以及解題技巧就是分類討論的解題思想.
在具體解題中,通過分類討論進行劃分的時候,需以劃分對象自身的相同或不同處作為依據,并根據其相同點以及不同點,將其分成不同種類,這不僅有助于學生進行更好的比較,而且還能準確找出其差異,并將有相同點的問題劃分到一個組別,這通常能夠使學生更有效的掌握相關數學問題間的聯系.
1.2 分類討論在數學解題中的應用價值
在高中數學的解題中,分類討論的思想運用通常有著重要價值.首先,有助于學生自身解題能力的提高,通過分類討論引導學生厘清數學題當中存在的數學關系,以此對數學題目進行準確解答,并在該過程中,促使學生對數學試題當中存有的數學思想深入理解;其次,有助于高中數學的課堂教學水平提高,并使學生在課堂上的學習難度得到有效降低.在高中數學的解題中,通常對學生自身的思維能力具有較高的要求,在實際解題中,通過分類思想的運用,不僅能夠有效解決學生在解題過程中遇到的難題與困難,而且還能使學生在具體操作中,形成自身獨特的分類思維,從而使學生的解題能力得到顯著提高.同時,將分類討論運用于數學解題中,可通過“化整為零、積零為整”的教學形式,不僅可以使學生構建自己對相關數學問題進行有效解決的機制,而且還能使學生對相關數學知識的邏輯性以及敏銳性得到有效提高,從而確保學生能夠靈活的學習相關數學知識,解決相關數學問題.
1.3 分類討論在數學解題中的應用原則
首先,統一性原則.高中數學的課堂解題中,數學教師需注重分類討論,并注重以統一分類的解題標準開展,避免同時運用多樣分類方法.比如,對三角形實施分類的時候,若將其分為銳角、直角、等腰、鈍角、不等邊三角形,由于該分類當中出現了兩種不同的分類標準,這種狀況下的分類結果就是錯誤的.
其次,互斥性原則.高中數學的解題中運用分類討論的方法,數學教師需充分明確在分類后每個子項的關系是互相排斥的關系,并保證分類之后的子項之間是無法相容的.
最后,層次性原則.高中數學與的解題中運用分類討論的解題思想,通常包含一次分類討論以及多次分類討論.對于一次分類討論而言,其通常指討論的數學問題只要開展一次分類即可;而對于多次分類討論而言,其主要指討論的數學問題需實施多次分析,直至符合相關要求.
2 分類討論思想下高中數學解題應用策略
2.1 基于分類討論的函數問題解答
分類討論不僅是一種數學解題方法,而且還是較為常用的一種數學思想,對數學方法進行科學合理的運用,通常能夠使數學題的解答更清晰靈活.分類討論的解題思想運用于數學問題解答中,有著重要地位,因此,在函數問題解答中,分類討論的運用,首先需對函數問題實施處理與觀察,若該問題不能通過統一的方法實施研究與解答,則需對該研究對象實施劃分,將整體分為幾個部分實施解答,即分類討論.運用分類思想時,需確保研究對象的準確劃分,避免條件疏漏或缺失,保證問題解答的準確性與完整性.函數作為高中數學解題中占比較大的部分,在對函數進行學習時,需對函數組成的部分實施分析,對于不同自變量,其通常對應著不同函數,通過函數運算,又會產生不同的結果.
例1(對函數問題中的變量x進行分類討論)求函數y=|x+1|+|x+2|-2的值域.
2.2 基于分類討論的數列問題解答
在高中數學數列問題教學中,數列周期性和等比數列求和等相關問題都和分類討論相關,學生通過分類討論的解題思想運用對數列問題的解答思路進行整理,并清楚地認識到題目當中是概念劃分、條件劃分、集合劃分,以此將問題清楚地分為不同狀況實施解答,因為部分數學知識在進行定義的時候,會依據分類概念實施,因此,學生在對有關數學問題進行解答的時候,需注重分類討論.通過分類討論的解題思想,不僅能夠使學生形成謹慎的邏輯以及嚴密的思維,而且還能使學生通過大量的習題練習,充分理解與掌握該解題思想的運用方式與本質,并對分類的規律進行總結,從而使學生更好的解決相關數學與問題.
例2假設首項是正數的等比數列{an}公比是q,前n項和為Sn>0(n=1,2,3,…),那么q的取值范圍是____.
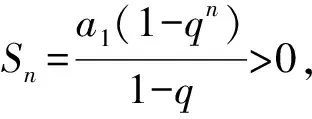
2.3 基于分類討論的概率問題解答
分類討論的解題思想,是高考中對學生的學習能力進行考查的重點,學生需善于分析與思考,通過分類討論對復雜的概率問題進行解答,并使條件不清晰的相關數學問題更加清晰明了.將分類討論的解題思想運用于概率問題解題中,通常能夠使概率事件的分類更清晰.在對概率問題進行學習時,其主要的內容就是引導學生充分了解、掌握相關概率事件的集合與某件事在全部事件中的具體發生概率,不論是分母,還是分子,通過分類討論的正確運用,對概率計算的正確性有著重要影響.在對概率相關問題進行解答時,學生需注重對事件的分析不遺漏且不重復,對分類對象進行清晰掌握,并通過統一化的分類標準,確保分類討論解題思想的準確應用.
例3某地的奧運會火炬傳遞活動中,共有編號是1,2,3,4,…,18的共18名火炬,從中只能選擇出3名擔任火炬手,選擇的火炬手編號通常能形成公差是3的等差數列的概率是( ).
A.151 B.168 C.1306 D.1408
解析該試題中,其不僅涉及到概率問題,而且還涉及到數列知識,學生在具體解題中,通過分類討論梳理好相應的解題思路,首先,對問題的概型實施整理,該問題是古典概型的問題,求取基本事件,就是總情況是17×16×3.然后,根據相關規律選出相應的火炬手,即a=1的時候,火炬手的選擇方式有幾種;b=2的時候,火炬手的選擇方式有幾種;c=3的時候,火炬手的選擇方式有幾種.經過分類討論的狀況相加,得出概率是168,故選B.
2.4 基于分類討論的不等式問題解答
高中數學的具體教學中,其難點通常是不等式求解,該類型數學題通常對高中生而言具有相應的難度.在這種狀況下,數學教師在實際教學時,就需注重分類討論解題思想的運用,以促使學生在對不等式問題實施解答時,能夠應用分類討論,這不僅可以使學生自身的解題思路更加清晰,而且還能使學生的解題能力以及解題效率得以顯著提高.
例4已知函數f(x)=|x+a-1|+|x-2a|,當f(1)<3時,求實數a的取值范圍.
解析首先,根據f(1)<3可得,|a|+|1-2a|<3,并對a實施分類討論,第一,當a≤0的時候,可得:-a+(1-2a)<3,對其使求解,得出:a>-2/3,以此得出結果:-2/3 綜上所述,在高中數學的解題教學中,分類討論的思想運用通常是有效且普遍的解題方法,這不僅可以使學生有效解決相關數學問題,而且還能確保學生準確解決問題的同時,實現解題效率的提高.因此,學生只有充分掌握分類討論的思想標準,才能促進其自身數學能力的增強.將分類討論的思想運用于高中數學的解題教學中,教師可積極引導學生理解與運用該思想,以促使學生在分類討論過程中,形成良好的邏輯思維,并實現學生全面發展.

