巧妙換元 解決難題
——換元法在高中數學解題中的應用
李志明
(甘肅省慶陽市正寧縣第四中學 745307)
換元法作為高中數學解題教學中應用較為廣泛的一種解題思想,其主要特點是化繁為簡,是在較為復雜的數學式子當中,通過新變元對原先式子中的復雜部分進行替換或者改造,簡化原式子,進而幫助學生解決問題.換元思想的本質就是轉化,換元能夠將原先問題由高次轉變為低次,將無理式轉變成有理式,超越式轉變成代數式,經過換元能夠促使數學問題從難變易,從繁變簡.將換元法應用于高中數學的解題中,學生就能根據知識之間的內在聯系,對相關數學題當中存有的數量關系進行轉化,把未知問題轉變為已知問題,通過問題及解題過程的簡化,使學生實現高效解題,促使學生的思維力得到明顯提高.
1 換元法概述
1.1 換元法的內涵
換元法主要就是指將數學題目當中的部分復雜內容通過另外的變量實施等效替換,形成原式的簡化形式,或是縮減原題目變量,使得問題簡單易解.一般來說,換元方式中比較常見的形式有三種,即(1)整體換元.比如把x的表達式f(x)從整體上替換為t,經過t表示為與x相關的新表達式;(2)通過有關的關系,通常指把具有較高相似度的表達式實施換元,經過已知的三角知識以及代數式之間存在的關聯實施換元,即在具體解題時,使用同樣的參數,表示不同的變量,以此減少變量,實現問題的簡單化;(3)均值換元.在能夠明確地求出變量和時,就可以應用均值換元.
1.2 換元法的應用技巧
第一,熟練掌握常規化換元法.面對不同的換元方法,一般都有對應的形式,尤其是數學中的三角換元.基于此,就難度相對較低的數學題來說,學生只有有效理解與掌握一般換元規律,才能做出及時且迅速的反應,更好更快地完成數學題的解答.
第二,注重引導學生觀察數學題的形式.對于具有較高難度的數學題來說,題目中一般會包含一些隱含條件,此時,教師需引導學生對數學題目的相關條件進行分析與梳理,以此為基礎,找出換元的突破點.需特別注意的是,數學題具備的難度一般不會影響到換元時的條件.基于此,對數學題的條件進行分步驟計算,不僅能夠開闊學生自身的解題思路,而且還能提高學生解題的準確率,實現高效解題.
第三,注重等效條件.換元法在應用前后的等效性一般是確保正確解題的關鍵,但這也是數學解題中極易容易被忽視的部分,不論是什么題型,有著什么難度,這都需學生牢固遵循換元條件的等效性.
2 換元法在高中數學解題中的應用策略
2.1 換元法在方程問題中的應用
高中數學的教學內容中,方程屬于基礎性知識,與方程有關的題目通常貫穿整個高中數學階段.但是,數學方程通常有許多種類,涉及到的知識點也有很多,特別是結構相對復雜的方程,這就會造成解題難度的提高.基于此,在方程解題時,數學教師需引導學生運用換元法,把相關方程類題目進行簡化,這不僅能實現解題難度的降低,而且還能使解題效率得到顯著提高.
例1設[(x4+2x2+1)/x2]+[(x2+1)/x]-2=0,求x的值.
解析在對該題進行解決時,通過換元法的應用,對方程進行轉化,將其轉變成[(x2+1)2/x2]+[(x2+1)/x]-2=0,令t=(x2+1)/x,構造新的方程t2+t-2=0,通過計算可求得:t1=-2,t2=1.然后,開展分類討論,t1=-2時,其方程則為x2+2x+1=0,此時x1=x2=-1.通過檢驗可得,該方程的解為-1.若t2=1時,其方程則為x2-x+1=0,其方程是不能求解的,由此可知,方程的解為-1.
評析通過上述例題可知,換元法的運用,將原先較為復雜且高次冪方程轉化為低次冪的方程,原先的一元四次方程則被轉變成一元二次的方程,該數學題的整體難度就會相應降低,省去了較多非必要的解題步驟.
2.2 換元法在不等式問題中的應用
在高中數學解題中,不等式的證明問題通常是學生解題中的難點.大部分學生在解決不等式問題的時候,都感到極其苦惱,不能夠找出合理切入點,解題條件不足.而通過換元法的運用,可提供給學生全新切入點,這不僅能夠使學生的解題思路更加清晰,而且還能使解題方式更加簡單.
例2已知[(x-1)2/9]+[(y+1)2/16]=1,設x+y-k>0成立,求k的取值范圍.
解析經過換元法的運用,對方程實施轉化,可設(x-1)/3=cosα,(y+1)/4=sinα,由此可知,x=1+3cosα,y=-1+4sinα.把x與y代入至x+y-k>0當中,就能計算出3cosα+4sinα>k.因為3cosα+4sinα=5sin(α+φ)>k,從而計算得出k<-5時,不等式恒成立.
評析通過上述例題分析,將新元代入題目條件當中,就能使不等式當中的原先變量條件不斷展現,將其作為基礎,展示全新表達式,有效運用到不等式證明當中,以實現數學題解題思路全面簡化.通過換元法的運用,不僅能準確地找出解題切入點,促進解題準確率的提高,而且還對題目證明的后續討論實施引導,以促使學生實現高效化解題.
2.3 換元法在函數值問題中的應用
在高中數學解題教學中,求函數最值問題通常是比較常見的,對該類型的題目進行有效學習,對于培養學生的解題能力有著顯著作用.一般來說,函數最值問題主要就是考察學生對于函數定義域、值域等相關知識的掌握,在對具體問題進行解答時,最重要的就是明確函數的取值范圍,然后對函數及變量的關系有效把握,以此實現數學問題的有效解答.
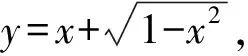
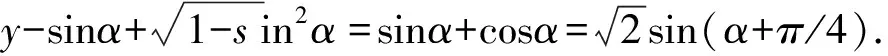
評析本題的解答是以新元代換的形式,促使原先看似較為復雜化的變量關系轉變為更加清晰的簡單變量關系,并對原先式子的取值范圍實施相應的簡化,以促使數學題的解題難度有效降低.通過換元法的運用,對函數值的問題進行求解時,核心就是找出新元的具體切入點,以完成相應的代換工作.
2.4 換元法在輔助函數換元構造中的應用
輔助函數的換元構造是相對重要的解題法,函數屬于高中階段數學教學當中極其核心的知識點,該部分知識通常有著明顯的工具性以及導向性,在大多數的數學問題解答中,都需要將函數作為輔助,以此更好地實現復雜且難以解決數學問題的轉化,促進教學思維的程序化.
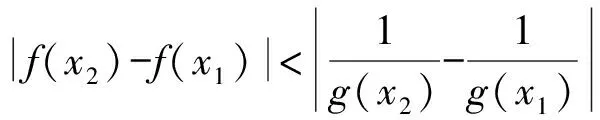
解析若m=1,a<0的時候,f(x)=x-aInx-1,x∈(0,+∞)
由于f’(x)=x-a/x>0位于[3,4]上恒成立,那么,f(x)位于區間[3,4]上呈現增函數.
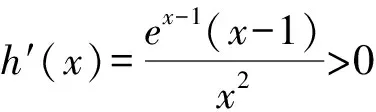
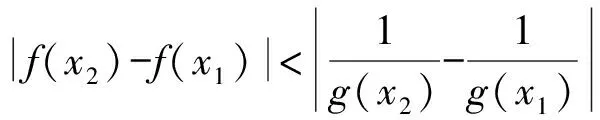
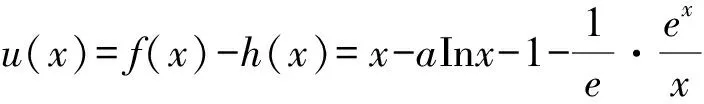
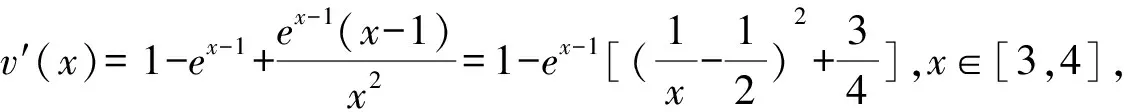
經過輔助函數的構造方法對上述例題進行解答,可明顯使原先的數學問題與輔助函數二者的聯系更加明確,經過相應的推理,進行輔助函數的構造,從而實現數學問題的高效化解決,并促使學生的解題效率得到顯著提高.
綜上所述,在高中數學的解題教學中,換元法屬于比較常見且實用的一種解題方式,其通常能夠使相對復雜的數學題得到有效處理與解答.因此,數學教師在教學時,需注重引導學生分析與探究換元法,對數學題目的相關條件進行合理分析,以實現換元法的靈活運用,促使學生的解題效率得到明顯提高.

