一題一課 以題研課

江蘇省宜興市張渚高級中學

陳云明

課堂是教學的主陣地，數學課堂應該有一定的廣度、深度，特別是高三復習課，更要精心選好試題，針對知識點，完善知識結構，激活學生思維，提升探究能力.其中，“一題一課”教學是高三數學復習課中一種非常重要的表現形式，對“題”進行深度挖掘，以“原題”為本，根據學生的認知規律和知識結構，合理設置，巧妙引導，從多層面進行“一題多解”嘗試，從多角度進行“一題多變”創新，由淺入深，做一題，得一法，會一類，通一片.

1 一題多解

一題多解是在教師精心挑選下，利用同一道題目引導學生用不同的思維方法來破解，利用發散、聯想、類比等思維方法對題目進行多角度、多方位的分析與思考，利用不同的知識、方法、工具等來分析與處理問題.一題多解能有效促進數學知識之間的聯系，提升數學思維能力、創新能力與應用能力等.

例1(2020年高考數學江蘇卷第11題)設{an}是公差為d的等差數列，{bn}是公比為q的等比數列.已知數列{an+bn}的前n項和Sn=n2-n+2n-1(n∈N*)，則d+q的值是______.

分析：此題是以兩個特殊類型的等差數列與等比數列加以融合與交匯，結合數列{an+bn}的前n項和的表達式來確定對應數列的公差d與公比q的和式的值問題.

思維視角一：代數運算.

解法1：(代數運算法)當n=1時，S1=a1+b1=1-1+2-1=1；

當n≥2時，an+bn=Sn-Sn-1=n2-n+2n-1-[(n-1)2-(n-1)+2n-1-1]=2n-1+2n-2.

則有a2+b2=22-1+2×2-2=4，a3+b3=23-1+2×3-2=8，a4+b4=24-1+2×4-2=14.

于是a1+d+b1q=4，a1+2d+b1q2=8，a1+3d+b1q3=14.

將a1+b1=1與以上三式依次對應相減，可得

d+b1(q-1)=3，d+b1q(q-1)=4，d+b1q2(q-1)=6.

即b1(q-1)=3-d，b1q(q-1)=4-d，b1q2(q-1)=6-d.

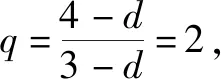
故填答案：4.

點評：通過n的分類討論以及數列{an+bn}的前4項的確定，結合a1+b1=1與相應的關系式進行代數運算，并結合條件關系式的轉化建立相應的方程，從而得以確定d與q的值.其實，在確定an+bn=2n-1+2n-2時，分別利用等差數列與等比數列的函數性，直接得以確定an=2n-2，bn=2n-1，進而確定公差與公比的值，在解決小題時可以這樣處理，節省時間.

思維視角二：公式應用.

解法2：(對比系數法)設等差數列{an}的公差為d，等比數列{bn}的公比為q，根據題意知q≠1.

則等差數列{an}的前n項和公式為

等比數列{bn}的前n項和公式為

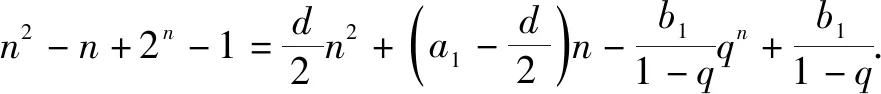
所以d+q=2+2=4.

故填答案：4.

點評：根據等差數列與等比數列的前n項和公式建立相應的關系式，結合條件Sn=n2-n+2n-1，通過對比相應數列求和中的系數關系建立對應的方程組，進而得以確定相關參數d與q的值.

2 一題多變

一題多變是在教師精心安排下，在實際教學過程中，以一道典型例題為模板，在解決問題的基礎上再從多角度、多方位、多層面等思維視角提出不同的問題，以進一步加深學生對知識的理解和掌握.一題多變能有效促進數學知識、思想方法和能力的融會貫通、舉一反三、觸類旁通，培養創新思維與創新意識，提升創新能力與核心素養.

故選：D.

變式方向1：改變題目中的相關數據，難度相當.

故選：B.

變式方向2：改變圓錐曲線的類型，難度相當.

故選：B.

變式方向3：改變題目已知條件，難度相當.

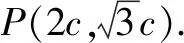
通過“一題多變”，培養學生的轉向機智及思維的應變性，實現提高發散思維的變通性.

“一題一課”教學，借助一題多解，一題多變等方式，合理達到一題一練一測一思一小結.以問題驅動為導向，教師體現主導作用加以合理引導.充分體現學生的主體地位，知識盡可能讓學生回顧，思路盡可能讓學生探尋，方法盡可能讓學生尋找，變式盡可能讓學生嘗試，從而真正實現知識回顧問題化，思路探尋發散化，方法尋找多樣化，變式嘗試創新化，全面提升數學能力，提高思維品質，培養數學核心素養.