基于PCK視角的高中數學概念教學研究
江蘇省蘇州實驗中學
王 莉
1 引言
數學概念能夠從本質上反映知識點,多數的數學知識都會圍繞特定的核心概念展開.概念教學是高中數學教學體系中的重要版塊,通過概念教學旨在讓學生形成對概念以及基本思想的理解.學科教學知識(PedagogicalContentKnowledge,PCK)的概念最早由美國教育研究會主席Shulman提出,他指出在教學中知識基礎共有七類,其中學科教學知識是重點與核心.他主張將教學學科的內容與教育學知識相結合,根據不同的教學知識內容的差異化使用教學方法與策略.筆者基于相關理論以及前人研究,以“任意角三角函數的概念”為例,探究PCK視角下高中概念教學設計的相關問題,以期為廣大師生提供教學參考.
2 掌握教材,了解學生,熟練教法
教材是教學活動最主要的依據,是知識內容最重要的來源.在研究教材時,教師要充分結合課程標準要求,認真思考教學目標,思考教學內容與全章節甚至是整本教材內容之間的關聯性,明確教學重點與難點,仔細研判例題與練習題,判斷能否延伸拓展.在備課過程中,除了要利用好教材,教師還需要借助課程標準、教輔資料、互聯網教學資源等補充教學內容.
學生個體之間存在較大的差異性,在概念教學的過程中,教師要根據學生的特點,強化概念形成過程的講解,引導學生用適當的方法參與學習.同時,教師還需要準確評估學生已有的知識能力水平,牢牢把握教學的起點.除此之外,教師還需要關注學生的情感與態度,加強德育教育,引導學生全面發展.
在明確教學內容和學生特點的基礎上,教師還需要選擇合適的教學方法,預先設計好概念引導的方式.比如,是采用形成還是同化的模式來講解相關概念;思考如何讓學生參與概念形成的探究過程,充分理解并合理運用概念.課堂教學方法科學與否不僅會影響學生對概念原理的掌握,也會影響學生數學思維的形成與發展.
3 構建概念教學結構體系
基于PCK視角的概念教學更加注重概念之間以及與其他數學知識之間的關聯性,因此在完成以上教學準備工作后,教師還需要深入挖掘,從更大的內容體系背景下優化教學方案.隨著教學內容的深入以及學生自身年齡的增長,學生對于復雜、抽象的數學概念的接受能力增強,思維整體性也不斷提升,因此教師在開展概念教學的過程中,不僅需要幫助學生掌握相關概念內涵,還需要提升學生思維的整體性,加強學生對宏觀知識架構的認知與理解,引導學生在一定知識積累的前提下,借助自己的認知構建網狀的知識框架,串聯相互關聯的知識內容.
4 強化數學概念的形成教學
概念教學的基礎環節就是概念引入,主要有“直觀引入”和“實際需要引入”這兩種方式,這一步會直接影響學生對概念的理解.“直觀引入”需要結合現實事例或者是客觀物體,減弱概念的概括性、抽象性給學生造成的干擾,幫助學生真正理解概念的內涵以及蘊含的數學思想,加深記憶,強化理解.比如在講授“概率”的概念時,可以借助拋硬幣、我國人口普查等實例來激發學生對概率的初步理解,通過“提出問題—結合實例—引發思考—概括概念”的教學過程引導學生充分參與概念的生成過程,加強直觀感受;“實際需要引入”則是強化相關概念的實際問題背景,常用的教學思路就是結合數學史來開展概念教學,將特定需求以及相關概念結合起來,加深學生對數學知識應用的認知.
在引入概念之后,需要強化學生對概念的理解,這是PCK視角下概念教學的核心環節.教師需要借助不同的問題情境、例題等突出概念的本質特征,多層次、全方位地進行概括,在此基礎上引導學生基于個人理解,用簡潔的語言來描述相關概念的特征并注重與其他概念的比較.在理解概念之后,還應設計概念鞏固的教學環節,讓學生自行敘述對概念的理解,向學生提出容易混淆的概念要點,鞏固概念教學的成果.
5 教學設計——以“任意角三角函數的概念”為例
基于PCK的內涵,筆者以“任意角三角函數的概念”教學為例,通過“教材及學情”“目標與重難點”“教學過程”等環節的研究,探究PCK視角下高中數學概念教學的實施路徑與改進策略.
5.1 教材及學情
“任意角三角函數”是人教A版必修一第五章第二節的教學內容,是對之前所學函數概念的補充與延伸,也是后續誘導公式、三角函數圖象與性質、和差公式等教學內容的前提,因此具有重要的銜接作用.在初中階段,學生已經接觸過銳角的三角函數,具有一定的知識基礎,但是也要讓學生明白二者的差別.銳角三角函數是指直角三角形中不同邊之間的比值,而任意角的三角函數則是指角終邊上一點的坐標與圓的半徑或者坐標之間的比值,這是任意角的三角函數與之前學生接觸的銳角三角函數概念的最大區別,也是本節概念教學的基礎.
5.2 目標與重難點
對于“任意角三角函數的概念”這部分內容,要求學生區別于銳角的三角函數概念,準確定義,能夠用坐標系中角的終邊和單位圓的交點坐標來表示,明確三角函數在不同象限的正負特征.任意角三角函數的概念以及定義域是本節教學的重點,難點為明確三角函數的內在關聯性.
5.3 教學過程
5.3.1 創設情境背景
地球的自轉公轉、月亮的圓缺變化、物理中的圓周運動、時鐘指針轉動,這些變化過程都具有交替往復的特征,為了準確描述任意的運動特征,將初中0°~360°的角度范圍進行延伸,擴大至任意角.假設單位圓O上的點M,以A為起點按逆時針方向運動,如果∠AOM=α,那么就可以用α來描述M點的位置.
設計意圖:不同于初中階段利用直角三角形來引入三角函數的概念,基于PCK理念,利用學生所熟悉的學科知識或者是生活現象創設情境,用圓周運動來引入教學內容,同時也能加深學生對于多學科交叉思維的認知.
5.3.2 引導探究
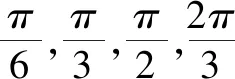
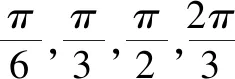
5.3.3 重難點解析

設計意圖:三角函數的定義域是本章的教學重點,其中正切函數的定義域又是難點.基于PCK理論視角,教師需要具備豐富的學科知識,能夠準確把握教材中的重難點并設計相應的教學環節進行突破.
5.4 改進策略
基于學科教學知識(PCK)的概念教學需要教師不斷總結教學過程,對教學目標以及重難點的形成準確判斷,并充分結合班級學生的學習訴求,認真反思,及時調整教學策略,不斷豐富自身的學科教學知識,優化其結構;同時,也要及時更新與教學相關的技術與手段.

