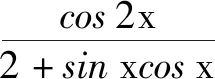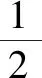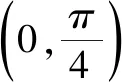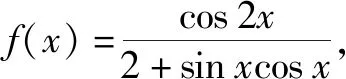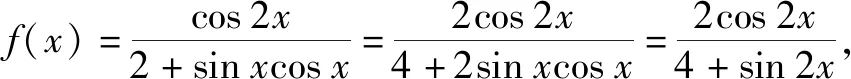強化三種意識 提升復習效率

江蘇省張家港市梁豐高級中學

陳慶菊

高三二輪復習是在第一輪對高中數學的基礎知識等的回顧與梳理的基礎上，全面開展的專題性、系統性的復習.高三二輪復習的目的就是進一步完善考生的數學知識體系與數學知識結構，并在此基礎上不斷總結破解數學問題的思想、意識、方法以及全面提升破解問題的能力等.合理強化數學意識，增強思想方法引導，全面深入二輪復習.結合2022年普通高等學校招生全國統一考試模擬演練(八省聯考)數學試題加以實例剖析，借助強化高三二輪復習的三種意識，有效增強復習效果.

1 函數意識

例1[2022年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·8]已知a<5且ae5=5ea，b<4且be4=4eb，c<3且ce3=3ec，則( ).

A.c

C.a

分析：利用題目條件中給出的指數關系式的恒等變形轉化，根據代數式的結構特征合理構建對應的函數，強化函數意識.通過函數的構造，結合函數的求導運算以及函數的單調性確定對應的參數值的大小關系.強化函數意識，巧妙破解大小比較問題.

同理可得f(4)=f(b)，0

由于函數f(x)在區間(1，+∞)上為增函數，則有f(5)>f(4)>f(3)，故f(a)>f(b)>f(c).

結合函數f(x)在區間(0，1)上為減函數，所以0

故選：D.

點評：函數意識包括數學中的函數與方程的轉化、構造函數、回歸函數本質等函數應用意識.借助函數意識，結合函數中的代數運算，以及函數的圖象與性質等相關內容，合理融入數學抽象、數學運算、直觀想象等相關的核心素養，融合“函數”與“圖象”加以數形結合、巧妙運算、合理轉化等.

2 互化意識

例2[2022年普通高等學校招生全國統一考試模擬演練(八省聯考)數學·6](1+x)2+(1+x)3+……+(1+x)9的展開式中x2的系數是( ).

A.60B.80C.84D.120

分析：利用題目條件中給出的二項展開式，巧妙借助二項式中各項的通項公式的對應規律，強化互化意識.結合等比數列的定義以及求和公式加以合理轉化，根據最終和式的特征確定相關二項展開式的系數，實現本質轉化，巧妙破解.

故選：D.

點評：互化意識包括數學中的定義轉化、結論轉化、圖形轉化、整體轉化、變換主元、正難則反等化歸與轉化意識，有時還可以是不同數學知識之間的聯系與轉化.借助巧妙的互化意識，把陌生的、不易解決的問題轉化為熟知的、易解決的問題來處理，整合數學知識，合理數學建模，改變思維角度，達到有效巧妙處理的目的.

3 導數應用意識

A.f(x)=f(x+π)

分析：根據題目條件中的三角函數解析式，結合三角函數的誘導公式的應用來證明關系式f(x)=f(x+π)的成立；利用三角函數關系式的恒等變換，巧妙借助三角函數的輔助角公式加以應用，結合三角函數的圖象與性質來確定函數f(x)的取值范圍；通過強化導數應用意識，利用函數的求導，結合導函數的符號來判斷函數在給定區間上的單調性.強化導數應用意識，為破解一些與函數有關的問題提供更為廣闊的空間.

故選：AD.

點評：導數應用意識包括數學中的函數與導數的關系、導數的運算、導數的幾何意義、函數的單調性或極值或最值、函數圖象等導數應用方面.借助導數應用意識，可以有效破解與函數有關的一些綜合問題；借助導數運算，巧妙轉化，合理應用，提升破解問題的效率與能力.

借助強化函數意識、互化意識、導數應用意識以及開放命題意識這三種意識，增強高三二輪復習的“靈魂”，在有效夯實“三基”(基礎知識，基本方法和基本能力)的前提下，以數學思想、意識、方法為引領，真正在數學解題能力與解題技巧等方面都有所提升，形成數學綜合能力.借助強化三種意識，可以有效引領并改進高三二輪復習的教學方式和方法，真正提升高三二輪復習效益，全面提升數學各方面的能力，培養數學核心素養.