導數中不等式問題常見的證明策略
浙江省諸暨中學暨陽分校
沈寶偉
導數中的不等式證明問題經常出現在高中數學解答題中,常常和函數零點、極值等不同知識點結合考查.導數中的不等式證明問題雖然難度較大,但有關解答問題的思路多種多樣.針對不同的問題,采取不同的解題方法,往往能達到事半功倍的效果.本文中將對3道不同例題進行分析,分別闡述證明導數不等式問題的四種不同解題策略.
1 構造函數法
利用構造函數方法證明導數不等式問題,主要是通過對不等式的變形加以構造函數.如,要證f(x)≤g(x)可以轉化為證明F(x)=f(x)-g(x)≤0.進一步對F(x)在對應區間的單調性和極值進行探究,得到F(x)值域的上界,就能證明原不等式成立.
例1已知函數f(x)=aex+2x-1,其中e是自然對數的底數.求證:對任意的a≥1,當x>0時,都有f(x)≥x(x+ae).
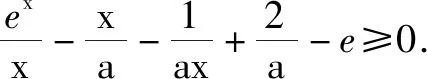

綜上所述,對任意a≥1,都有f(x)≥x(x+ae)成立.
思考:上述問題求解中,把證明不等式問題轉化為函數極值求解問題,正是借助了構造函數的方法和思路,具有一定的借鑒意義.應該注意的是,解題過程中,aex-x-1≥ex-x-1運用了放縮思想,使問題求解更直接,值得反復推敲并學習.
2 切線放縮法
所謂切線放縮法,主要指利用函數在指定點附近對應的切線在函數圖象的一側的特點,進行去指數化、去對數化,從而對導數中不等式證明問題進行求解.如求證xlnx≥asinx-1時,由于f(x)=xlnx在x=1處切線方程為y=x-1,且xlnx≥x-1,對此所證不等式可以轉化為x-1≥asinx-1,進而求證即可.運用函數切線特點放縮不等式,能使解題思路變得更加清晰直觀.
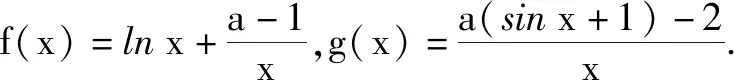
分析:通過簡化首先得到xlnx>asinx-1,此時對h(x)=asinx-1單調性進行分析,得到ax-1>asinx-1.由y=x-1是函數f(x)=xlnx在x=1處的切線,因此可以把y=x-1和y=ax-1進行比較,就可以證明f(x)>g(x).
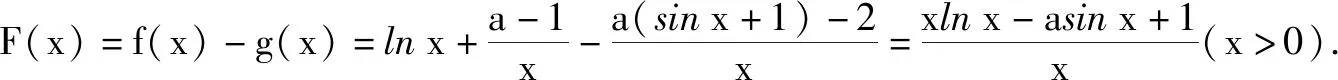
令h(x)=x-sinx(x>0),則h′(x)=1-cosx≥0,所以函數h(x)在(0,+∞)上單調遞增.故h(x)>0,即x>sinx(x>0).
于是當0
令m(x)=xlnx-x+1,則m′(x)=lnx.當x∈(0,1),m′(x)<0,函數m(x)在上(0,1)單調遞減;當x∈(1,+∞),m′(x)>0,函數m(x)在上(1,+∞)單調遞增.故m(x)≥m(1)=0,即xlnx≥x-1,當且僅當x=1時等號成立.
因為0 由xlnx≥x-1≥ax-1和ax-1>asinx-1(x>0),可得xlnx≥x-1≥ax-1>asinx-1. 所以,當0 主參互換方法的運用解答,關鍵在于把需要證明的不等式中參數與變量的位置關系進行互換,如證明f(x)≥a,可以結合具體解析式轉化為g(a)≤0的等價不等式,通過證明與參數有關的等價不等式成立,從而對問題做出具體充分的解答.主參互換思路的運用,能使不等式問題的解題過程更加直觀. 例3已知函數f(x)=ln(ax)-x+a,當0≤a≤1時,試證明:f(x)≤(x-1)ex-a-x+a. 分析:首先結合具體函數解析式將需要證明的不等式看作與參數a有關的等價不等式證明問題,即在0≤a≤1范圍內證明不等式ln(ax)≤(x-1)ex-a成立,考慮構造函數g(a),分情況討論x在不同取值范圍下g(a)的取值范圍,證明g(a)≥0,即可對問題做出解答. 解:以a為主元,不等式等價于 ln(ax)≤(x-1)ex-a, 令函數g(a)=(x-1)e-a+x-lna-lnx,則 ①當x≥1時,g′(a)<0,g(a)≥g(1)= (x-1)ex-1-lnx, 以x為主元,令函數h(x)=(x-1)ex-1-lnx. 故g(a)=(x-1)e-a+x-lna-lnx≥0. ②當0 令函數q(x)=(x-1)ex,由q′(x)=xex>0可知q(x)∈(-1,0); 由g′(a)<0,可得函數g(a)單調遞減,故g(a)≥g(1)=(x-1)ex-1-lnx. 故g(a)≥g(1)=(x-1)ex-1-lnx=0. 綜上,所證不等式成立. 分析最值方法的運用,主要體現在解題過程中把不等號兩邊的解析式分別看做兩個函數,如要證g(x)≥h(x)成立,即證gmin(x)≥hmax(x).分別對兩個不同函數的單調性和極值進行分析,進而證明所證不等式成立.具體解題方法在問題中的運用,如例4所示. 分析:要證不等式f(x)>lnx,可以看成f(x)>g(x)=lnx,分別研究f(x)和g(x)的單調性和極值,進而求出在(0,+∞)上f(x)的最小值和g(x)的最大值,就能證得f(x)>lnx成立.3 主參互換法
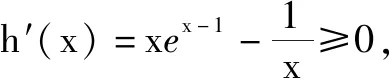
4 分析最值法