圓錐曲線焦半徑公式的進一步推導及應用

浙江省諸暨市草塔中學

金鐵強

橢圓、雙曲線的焦點弦或焦半徑的問題是解析幾何中的常規考點，很多老師在講解的時候喜歡用“設而不求”來解決問題.但用此法來處理焦點弦問題也有其弊端，一是步驟過多，二是有些問題不能直接用此法求解，必須再要用到“設而求之”才能解決.對于現在的多變題型，已經達不到通解通法的要求，因此有必要對圓錐曲線焦半徑公式進行進一步的挖掘和整理，才能適應當前高考題型的發展趨勢，讓學生能夠更直觀地解題.

1 焦點在x軸上的橢圓焦半徑公式的推導及應用

圖1

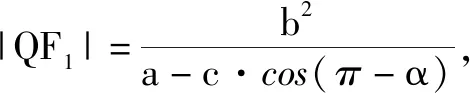
這個公式把焦點弦分成上下兩部分，每部分的焦半徑都有自己的表達式，這樣對于條件運用可以更直接明了.

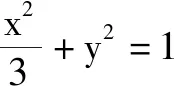
圖2

解析1雖步驟不多，但運算復雜.如果我們用焦半徑公式，整個問題就豁然開朗.

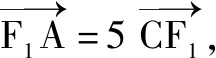
綜上可知：A(0，1)或A(0，1).

分析公式的本源可得出很簡單的結論，焦點弦的弦長及被焦點分開的兩段焦半徑的比例值其實與橢圓的形狀(即a，c的值)，與焦點弦所在直線的方向(即斜率k或傾斜角α)存在關系，即a，c，α三個量決定了焦點弦的一切，那我們不妨直接利用這樣的代數關系來解決問題，解題就方便多了.

2 焦點在x軸上的雙曲線焦半徑公式的應用

同樣地，該公式也適用于雙曲線.

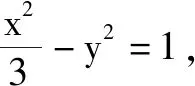
解析：由條件知，若焦點弦為一條交于雙支，一條交于單支，則不能構成四邊形，則兩條焦點弦都交于左支或都交于雙支.

利用公式直接代入，解題過程簡潔明了，優點顯而易見.

3 焦點在y軸上的圓錐曲線焦半徑公式

圖3

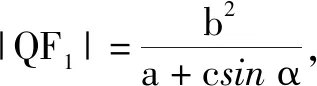
因此，簡單總結如下：