也談數學歸納法在解題中的應用
內蒙古巴彥淖爾市臨河區第一中學
薛思謙
1 引言
對于一類與正整數有關的命題的論證問題,當其他方法無法證明時,往往想到數學歸納法.用數學歸納法證明問題分三個步驟:第一步先證明當n取初始值n0(n0∈N*)時命題成立.這是第二步的前提,不可省去,初始值n0視題目而定,不一定是1.第二步先假設當n=k(k∈N*,k≥n0)時命題成立,在此基礎上,推證當n=k+1時命題也成立.這一步驟是數學歸納法最關鍵的步驟,要求對有關表達式進行恰當變形,而且在證明當n=k+1時命題成立時,必須以“當n=k時命題成立”為條件,否則是“假數學歸納”.第三步則由以上兩個步驟得出所證結論.這一步必須規范書寫,否則就不是數學歸納法.由此可見,數學歸納法不同于其他數學方法,它是一個特別注重書寫格式和過程規范的證明方法,這一點要引起大家的注意.在數學解題中,數學歸納法有著廣泛的應用.主要體現在以下四個方面:用數學歸納法證明等式;用數學歸納法證明不等式;用數學歸納法證明數的整除性;用數學歸納法證明猜想的結論.下文舉例說明.
2 用數學歸納法證明等式
對于有些與正自然數有關的等式的證明問題,當其他證明方法無能為力或過程太繁瑣冗長時,就可以采用數學歸納法.

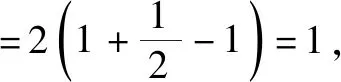
(2)假設n=k(k≥2,k∈N*)時,等式成立,即f(1)+f(2)+f(3)+……+f(k-1)=k[f(k)-1],上式兩邊同時加上f(k),得
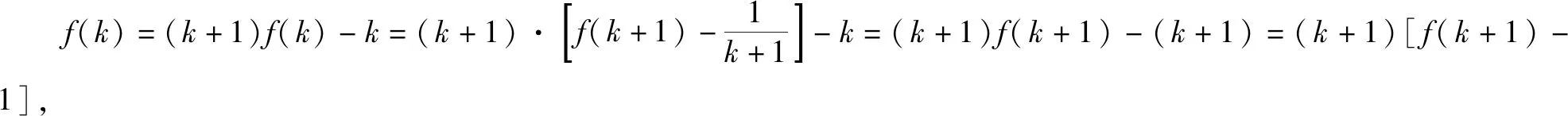
即當n=k+1時等式依舊成立.
由(1)(2)可知,f(1)+f(2)+f(3)+……+f(n-1)=n[f(n)-1]對n≥2,n∈N*都成立.
點評:用數學歸納法證明等式問題的關鍵點在于弄清所證等式兩邊各項的規律,等式兩邊含有的項數,初始值n0是哪個數.由n=k出發證明n=k+1命題也成立時,除了要考慮等式兩邊變化的項之外,還要充分利用n=k時的式子.
3 用數學歸納法證明不等式
用數學歸納法證明與n有關的不等式,通常出現兩種情況:一是直接給出不等式,按要求進行證明;二是給出兩個式子,按要求比較它們的大小.對第二類問題可先對變量n取最初幾個特殊值分別驗證比較,從而得出所證結論,最后再用數學歸納法證明這個不等式.

(1)證明:0 證明:(1)①當n=1時顯然成立; 綜合①②可知,0 點評:本題第(1)問用了數學歸納法,第(2)問用的是綜合法,請注意它們之間的區別.用數學歸納法證明不等式的關鍵還是由n=k成立,推證n=k+1時也成立,用了歸納假設后,可采用其他證明不等式的所有方法,如分析法與綜合法、比較法與放縮法等. 關于與正整數n有關的指數型代數式的整除性問題的證明,一般用到兩種證明方法:一是直接法,即構造二項式,并利用二項式定理將其展開進行證明;二是利用數學歸納法,嚴格按照數學歸納法的三個步驟加以論證. 例3試證(3n+1)·7n-1(n∈N*)能被9整除. 證明:(1)當n=1時,(3+1)×7-1=27能被9整除,故命題成立; (2)假設當n=k時命題成立,即(3k+1)·7k-1(n∈N*)能被9整除,那么 [3(k+1)+1]·7k+1-1 =(3k+1)·7k+1+3·7k+1-1 =7·(3k+1)·7k+3·7k+1-1 =(3k+1)·7k-1+6·(3k+1)·7k+3·7k+1 =[(3k+1)·7k-1]+(18k+27)·7k, 由歸納假設(3k+1)·7k-1(n∈N*)能被9整除及(18k+27)·7k是9的倍數,可得[(3k+1)·7k-1]+(18k+27)·7k能被9整除,即n=k+1時,命題成立. 由(1)(2)可知,命題對任意的n∈N*都成立. 點評:用數學歸納法證明整除性問題,關鍵還是在第二步,將[3(k+1)+1]·7k+1-1變形成[(3k+1)·7k-1]+(18k+27)·7k,考查等式的變形能力. 先歸納,再猜想,后證明,是一種不完全歸納法與數學歸納法“聯合作戰”的解題模式. (1)求f1(x),f2(x);(2)猜想fn(x)的表達式,并證明你的結論. 證明:①當n=1時,由(1)知猜想的結論正確; ②假設當n=k,k∈N*時,結論正確,即有 =(-1)k-1·ak-1·(bc-ad)·k!.[(ax+b)-(k+1)]′ 即當n=k+1時結論成立. 由①②可知,對一切n∈N*猜想的結論正確. 點評:本題的第(1)問,借助題設條件運用導數知識直接求解;第(2)問歸納法推證時,能借助(1)猜想結論,進而運用數學歸納法分析推證,從而獲證.本題證明的難點有兩個:一是猜想的結論不可有絲毫差錯,二是從n=k,k∈N*到n=k+1中的式子的變形. 本文最后值得一提的是,數學歸納法作為一種數學證明的方法,雖然用途比較廣泛,尤其是在高考壓軸題或數學競賽中,有著不可或缺的作用,但由于它的書寫格式要求比較高,所以建議慎用.當采用別的證法也能順利解決問題時,還是以其他證明方法為上策.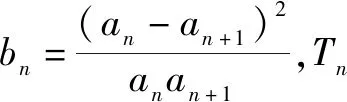
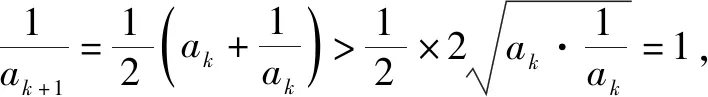

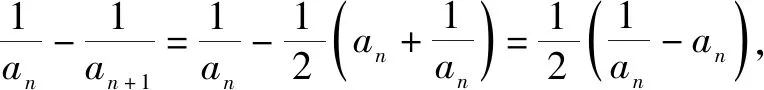
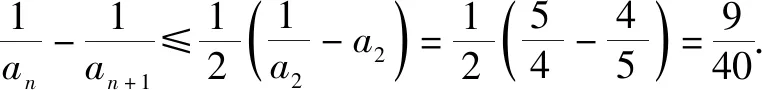

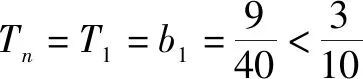

4 用數學歸納法證明整除性問題
5 用數學歸納法證明猜想的結論
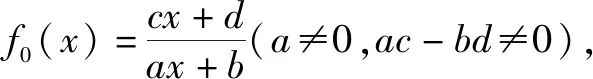


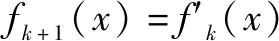
6 結語

