深入研究一節教材 精心設計導學方案
——以青島版“二次函數”的概念為例

?山東沂南第四中學 李樹臣?山東威海高區一中 韓 燕

1 引言

《義務教育數學課程標準(2011年版)》(簡稱《課標(2011年版)》)提出的提高學生的數學核心素養目標的落實，是通過每一節課堂教學逐步實現的.因此，教師應研讀每一節教材，把握每一節教材的編寫意圖，設計好教學方案，才能保證每一節課的教學質量.

據了解，很多老師的教案沒有體現出教材的編寫意圖，導致教學出現了“偏差”.這部分老師對教材研究的“力度”不夠，若長此以往，將很難保證實現《課標(2011年版)》的理念.

本文中以《課標(2011年版)》下青島版“二次函數”一節課的研究和教學設計為例，旨在說明教師首先應認真研讀教材，把握教材編寫的意圖，才能編寫出符合教材要求的導學方案.

2 研讀教材的收獲

數學教材凝聚了編寫者的心血，他們在編寫過程中，認真學習、反復推敲《課標(2011年版)》的每一條理論要求，耐心打磨教材中的每一句話(一個字)，在比較、斟酌中篩選教材中的每一個例題、練習題.

課堂教學的主要依據是教材.教師在教學前應反復閱讀，認真研讀，充分理解教材的編寫意圖.這對于指導教學具有現實意義.

教師只有反復研讀每一節(課)教材，才能把握教材的編寫意圖，明確教材的主要內容，從而確定教學目標，找出教學重點和難點，設計出切實可行的教學方案.

青島版教材九下“5.3二次函數”主要內容有5個問題、一個例題、兩個練習和6個習題.通過研究，可以把其分為三個主要環節.

環節1：二次函數的建立.

整個二次函數的建立過程分三個層次：

第一層次：問題情境導入.

教材在二次函數概念引入前，設計了三個問題：(1)用鐵絲圍矩形問題；(2)小球沿光滑斜坡滾動問題；(3)企業產值問題.

要求學生分別寫出這三個問題中變量之間的函數表達式.

編寫意圖:初中階段學生主要學習一次函數(正比例函數)、反比例函數和二次函數，在學習前面兩類函數時已經有了下述認知：(1)函數是刻畫變量與變量之間依賴關系的模型；(2)函數是聯結兩類對象的橋梁；(3)函數是“圖形”.對函數內容的呈現過程如圖1所示.

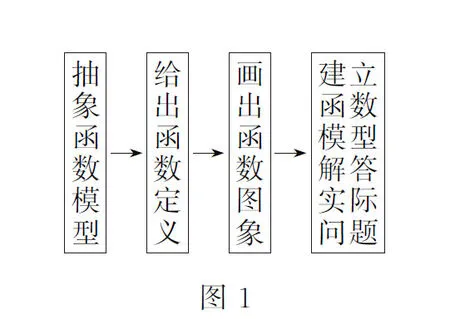
教材在這個基礎上，安排了“二次函數”的內容，本節“沿襲”學習前面兩類函數的研究過程.《課標(2011年版)》對“二次函數”的第一條要求是“通過對實際問題的分析，體會二次函數的意義”.結合《課標(2011年版)》提出的“現實性”要求，教材從“貼近學生的現實”出發，精心選取了上面的三個問題，其中問題(1)和(3)取材于“生活現實”，問題(2)取材于物理學科.

三個問題立足于學生的“生活現實”，有助于學生從“現實情境”中抽象出數學知識，進一步感悟“數學與生活”的關系，加深對模型思想的認識.這種設計符合“認識到現實生活中蘊涵著大量與數量和圖形有關的問題，這些問題可以抽象成數學問題，用數學的方法予以解決”的《課標(2011年版)》要求.

第二層次：抽象本質特征.

教材在這個階段的文字敘述很簡練，僅有三行字，形成了第(4)個問題：

經過整理，以上三個問題中的函數表達式分別是：

①y=x2+30x；②S=2t2；③W=1 200x2+2 400x+1 200.

觀察這些函數表達式，你發現它們具有什么共同特征？

設計意圖：史寧中教授指出“抽象是從許多事物中舍棄個別的、非本質屬性，得到共同的、本質屬性的思維過程，是形成概念的必要手段”.抽象能力是數學核心素養的重要組成部分，抽象能力是在學生經歷抽象的過程中形成和發展起來的.這個層次的意圖就在于培養學生從三個表達式的眾多屬性中抽象出“共同特征”的能力，從而發展學生的數學核心素養.

第三層次：引入二次函數概念.

一般地，形如y=ax2+bx+c(a，b，c是常數，且a≠0)的函數叫做二次函數.

你能分別說出上述三個二次函數表達式中的二次項系數、一次項系數和常數項嗎？

設計意圖：數學概念的教學既是數學教學的重要環節，又是數學學習的核心.其根本任務是準確地揭示概念的內涵與外延，使學生在思考問題、進行推理論證時能有據可依，并能創見性地解決問題.數學概念都有非常精確的含義，在第二個層次中，學生對三個二次函數表達式的本質特征有了認識后，教材及時給出了二次函數的定義.這里采用的是“形式定義”法，這種定義雖然能從其中分離出概念的內涵，按規則作外延分類，但又不是從內涵或外延出發而構造相應的模式，它的著眼點在于被定義概念的本質結構.

環節2：二次函數中自變量的取值范圍.

教材在這個環節設置了第(5)個問題：

(5)你能說出二次函數y=ax2+bx+c中變量x的取值范圍嗎？你能分別說出問題(1)(2)(3)中自變量取值的范圍嗎？

設計意圖：在引入二次函數定義后，明確自變量的取值范圍對學生理解二次函數以及后面利用二次函數的性質解決實際問題也具有積極的意義.另外，二次函數是用數學式子給出的，在二次函數y=ax2+bx+c的表達式中，每個字母符號都具有自己的意義.單就二次函數的表達式y=ax2+bx+c來說，自變量x的取值范圍是沒有限制的，x可以取任意實數.但對于從實際問題中抽象出來的具體二次函數表達式y=ax2+bx+c中的自變量必須確保實際問題有意義，這就客觀導致了自變量的取值不能“自由任性”，要受到一定的限制，這是學生學習中容易出現問題的地方.基于上面兩點，教材給出了問題(5)，學生通過思考、討論問題(5)可以達到上面的目的.

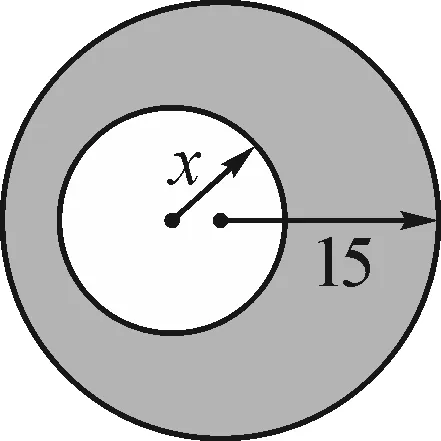
圖2

例題如圖2，從半徑為15的圓形鐵片上，挖去一個半徑為x的圓.寫出剩余部分的面積y與x之間的函數表達式，并指出自變量x可以取值的范圍.

設計意圖：這是一個實際問題，設計這個題目的目的是讓學生進一步明確二次函數與數學的關系，學會建立二次函數表達式，體會建立函數模型的過程，并且加深對自變量取值是有限制條件的認識.

3 二次函數的教學方案

有了上面對教材的研究，可以將“二次函數”這一課的宏觀教學方案設計如下：

(一)學習目標.

(1)結合具體情境，通過用表達式表示簡單實際問題中變量之間的函數關系，體會二次函數的意義.

(2)經歷二次函數概念的形成過程，體會二次函數也是一種數學模型.

(3)會把一個二次函數化成一般形式.

(二)重點難點.

重點：理解二次函數的有關概念，能應用二次函數的相關知識解決簡單的問題.

難點：將簡單的實際問題轉化為二次函數的模型.

(三)教學過程要點.

(1)回顧函數的概念，到目前我們學了哪些函數？你能說出它們的概念嗎？

(2)自主探究.

思考下列問題，并與同學們交流.

①把一根長為60 cm的鐵絲，圍成一個矩形.寫出矩形的面積S(單位：cm2)與它的一邊長x(單位：cm)之間的函數表達式.

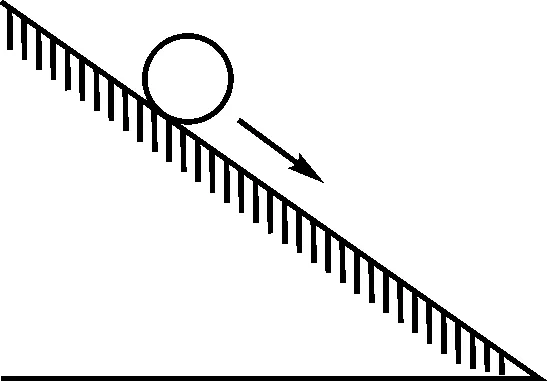
圖3

②一個小球由靜止開始，沿圖3所示的光滑斜坡向下滾動，經過5 s到達斜坡的底部.實驗測得小球滾動的距離s(單位：m)與時間t(單位：s)對應的數據如表1所示：

表1 小球滾動的距離與時間對應表

分析表1中的數據，并根據數據回答下面問題：

(ⅰ)當t增加時，s怎樣變化？

(ⅱ)s與t之間的函數表達式可能為.

③某企業去年的產值為1 200萬元.如果三年內該企業年產值平均每年的增長率為x，你能寫出明年該企業年產值y(單位：萬元)與x之間的函數表達式嗎？

(3)抽象歸納.

觀察下面三個函數表達式，它們有什么共同特征？

①y=x2+30x；②S=2t2；③W=1 200x2+2 400x+1 200.

(4)給出二次函數概念.

(5)例題講解.

講解例題時，可引導學生列出函數表達式，再由x表示小圓半徑，從而得到x>0.另一方面，由于小圓圓心可以與大圓的圓心重合，此時要使小圓在大圓內，x應滿足x<15.

(6)嘗試應用.

①分別說出下列二次函數的二次項系數、一次項系數、常數項.

(ⅰ)y=-x2+58x-112；(ⅱ)y=πx2.

②當系數a，b，c滿足什么條件時，函數y=ax2+bx+c是二次函數？一次函數？正比例函數？

③已知正方形的邊長是3，當邊長增加x時，面積增加y，寫出y與x之間的函數表達式.

4 兩點啟示

從前面的敘述看，只要在教材研讀方面下了功夫，把握了教材的編寫意圖，編寫教學方案就顯得很輕松，更重要的是這樣編寫出的教學方案才是有實效的.通過對青島版“二次函數”一課的教學研究，我們至少有以下兩點體會.

(1)加大研讀教材的力度.

首先，教師要樹立正確的“教材觀”.數學教學必須以教材為藍本，以教材為根本.要正確理解目前流行的“不是教教材，而是用教材教”“要創造性地使用教材”等“時髦”觀點.教學中教師一定要重視教材，研讀教材，不能脫離教材.有些老師企圖用所謂的“導學案”代替教材是很荒唐的做法.

其次，通過研讀教材正確把握教材的編寫意圖，這是教師編寫教學方案的基礎，只有這樣才能確保編寫的教學方案是針對教材的，確保教學真實有效，提高教學質量.

(2)概念教學應貫穿于課堂教學的始終.

數學概念是人腦對現實對象的數量關系和空間形式的本質特征的一種反映形式.數學概念是重要的數學基礎知識，是構成數學教材的基本結構單位，正是因為這些數學概念的存在，才形成了數學教材的知識結構.

曹才翰老先生說過，“概念是思維的細胞，數學根本上是玩概念的，不是玩技巧，技巧不足道也”.數學教學必須做到“概念明確”，因為在教學中只有明確概念，才能把握概念的本質屬性.數學公式、定理和方法都是反映數學對象和概念間關系的，學生只有建立起了正確明晰的概念，才能牢固地掌握基礎知識，進行命題推理.

數學概念貫穿于數學教學的始終，新授課離不開數學概念，復習課更是離不開概念，而一個個的數學知識點就是靠概念“串連”在一起的.通過復習欲達到系統掌握知識的目的，只要把本單元所涉及的概念串連起來就能“再現”教材的知識結構.所以，從數學教學的形式和內容上看，數學概念教學始終與課堂教學并存.

概念教學是培養學生思維能力的起始階段和基本出發點，學生在深入理解數學概念的過程中能使自己的抽象思維得到發展.可見，數學概念教學的質量，直接影響到學生思維能力的形成，關系到其思維能力的發展.所以，我們要把數學概念的教學融入到教學的全程之中.