鎖定已知 構(gòu)建聯(lián)系 設(shè)定未知 發(fā)展思維
——以“用一元二次方程解決問(wèn)題”課堂教學(xué)為例
?江蘇省無(wú)錫市江南中學(xué) 王 蕾
1 引言
“用一元二次方程解決問(wèn)題”是蘇教版九年級(jí)(上)第一章第四節(jié)的內(nèi)容.在本章的前三節(jié)學(xué)生已經(jīng)學(xué)習(xí)了一元二次方程的概念、解法,以及方程的解與系數(shù)的關(guān)系,對(duì)一元二次方程相關(guān)知識(shí)有了系統(tǒng)的認(rèn)知.接下來(lái)通過(guò)探究實(shí)際生活中數(shù)量關(guān)系的過(guò)程,體會(huì)、體驗(yàn)一元二次方程解決實(shí)際問(wèn)題的數(shù)學(xué)模型;同時(shí),在運(yùn)用一元二次方程解決現(xiàn)實(shí)生活中實(shí)際問(wèn)題時(shí),不僅要注意解方程的過(guò)程,還要檢驗(yàn)所得的解是否符合問(wèn)題的實(shí)際[1].
2 創(chuàng)設(shè)實(shí)際問(wèn)題情境,引導(dǎo)學(xué)生進(jìn)入課題
從字面上看“用一元二次方程解決問(wèn)題”這一課題有兩個(gè)方面的含義:一是運(yùn)用的知識(shí)是一元二次方程,另一是解決的問(wèn)題是現(xiàn)實(shí)生活問(wèn)題.因此,把實(shí)際問(wèn)題轉(zhuǎn)化為數(shù)學(xué)問(wèn)題,對(duì)現(xiàn)實(shí)生活問(wèn)題進(jìn)行數(shù)學(xué)建模,不僅僅是列出一元二次方程去求出問(wèn)題的解,而且還要進(jìn)行推理判斷所得出的結(jié)果與生活實(shí)際是否相符,這是本課題的重點(diǎn),也是本課題的難點(diǎn).
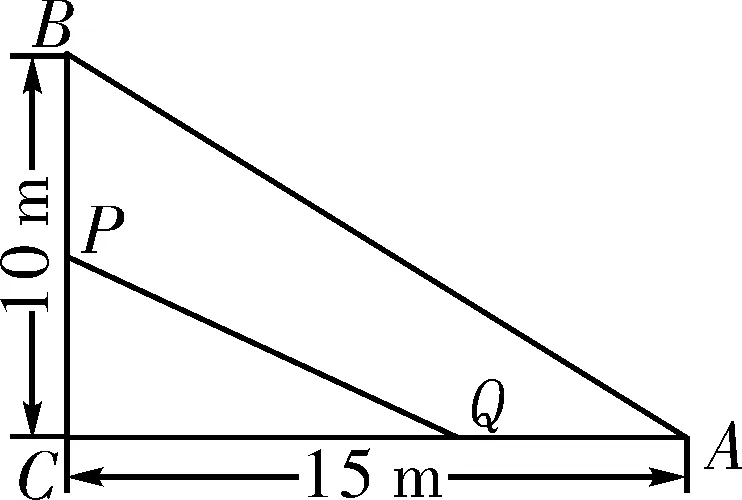
圖1
導(dǎo)入情境(電子白板展示)如圖1,Rt△ACB是一養(yǎng)魚(yú)池的一角,∠C=90°,為了捕魚(yú),一漁網(wǎng)同時(shí)由A,B兩點(diǎn)出發(fā)分別沿魚(yú)池邊緣AC,BC方向向點(diǎn)C勻速移動(dòng)至點(diǎn)Q,P,它們的速度都是1 m/s,問(wèn)多長(zhǎng)時(shí)間后△QCP的面積為Rt△ACB面積的一半?
創(chuàng)設(shè)目的:為了讓學(xué)生將實(shí)際問(wèn)題具體化,在引入課題之時(shí)創(chuàng)設(shè)的問(wèn)題情境用圖象形式呈現(xiàn),讓生活問(wèn)題具有“數(shù)學(xué)模型”化的特征,學(xué)生用數(shù)學(xué)方法建模就可以簡(jiǎn)單化.
3 引導(dǎo)探究解題過(guò)程,幫助學(xué)生對(duì)實(shí)際問(wèn)題進(jìn)行數(shù)學(xué)建模
“引導(dǎo)探究解題過(guò)程”“幫助學(xué)生進(jìn)行數(shù)學(xué)建模”是幫助學(xué)生掌握應(yīng)用一元二次方程解決實(shí)際問(wèn)題的方法步驟,并且是提高分析問(wèn)題、解決問(wèn)題能力的關(guān)鍵.
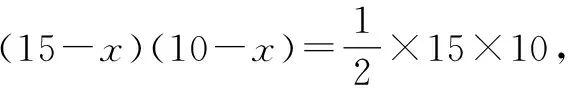
教學(xué)案例1
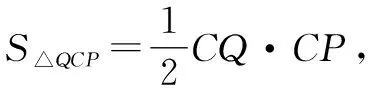
師:如何計(jì)算CQ,CP的值呢?
生:根據(jù)點(diǎn)A到點(diǎn)Q與點(diǎn)B到點(diǎn)P距離相等.(進(jìn)行討論、各抒己見(jiàn).)
師:若點(diǎn)A到點(diǎn)Q的距離是xm,又怎樣計(jì)算CQ,CP的值?
生:CQ=(15-x)m,CP=(10-x)m.
師:請(qǐng)同學(xué)們解決情境中的問(wèn)題.
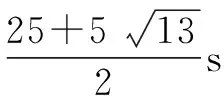
師:這兩個(gè)數(shù)據(jù)都符合實(shí)際情況嗎?
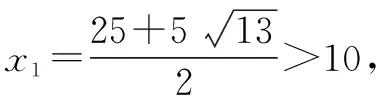
師:通過(guò)以上問(wèn)題說(shuō)明,利用一元二次方程解決問(wèn)題不僅要求出具體數(shù)值,而且還要分析判斷是否存在某種數(shù)量關(guān)系;同時(shí),用一元二次方程解決實(shí)際問(wèn)題時(shí),不僅要注意方程求得的解是否正確,還要檢驗(yàn)方程的解是否與問(wèn)題的實(shí)際情境相符合.請(qǐng)大家思考上述解決問(wèn)題的主要步驟.
學(xué)生:通過(guò)小組討論,歸納總結(jié)出:
①?gòu)那榫持姓页龃嬖诘牧康年P(guān)系,列出等式;
②在列出的等式中發(fā)現(xiàn)未知量,設(shè)定未知數(shù);
③將設(shè)定未知數(shù)代入列出的等式中進(jìn)行求解;
④檢驗(yàn)所得出的未知量與情境是否相符.
教學(xué)反思:通過(guò)案例分析不難發(fā)現(xiàn),這是一種探究、討論、啟發(fā)式的教學(xué)過(guò)程.在此過(guò)程中,教師一直引導(dǎo)鼓勵(lì)學(xué)生自主探究、合作交流,培養(yǎng)自覺(jué)思考的良好習(xí)慣,實(shí)現(xiàn)對(duì)實(shí)際情境問(wèn)題的數(shù)學(xué)建模.
4 驅(qū)動(dòng)內(nèi)化解題的潛能,強(qiáng)化學(xué)生對(duì)數(shù)學(xué)建模的解題應(yīng)用
對(duì)實(shí)際問(wèn)題的數(shù)學(xué)建模,其作用之一是規(guī)范學(xué)生的解題步驟,形成一種抽象思維的定式.因此,在課題的導(dǎo)入情境中作出相應(yīng)的變式,讓學(xué)生在已經(jīng)熟悉的情境中拓展思維是很有必要的.也就是說(shuō),對(duì)一節(jié)課的知識(shí)要鞏固,通過(guò)變式練習(xí)達(dá)成“堂堂清”[2].
變式情境(電子白板展示)如圖1,Rt△ACB是一養(yǎng)魚(yú)池的一角,∠C=90°,為了捕魚(yú),一漁網(wǎng)同時(shí)由A,B兩點(diǎn)出發(fā)分別沿魚(yú)池邊緣AC,BC方向向點(diǎn)C勻速移動(dòng)至點(diǎn)Q,P,漁網(wǎng)的速度分別是1.5 m/s,1 m/s,若△QCP的面積為Rt△ACB面積的一半,則需經(jīng)過(guò)多長(zhǎng)的時(shí)間?
教學(xué)案例2
生:不能直接設(shè)點(diǎn)A到點(diǎn)Q的距離或點(diǎn)B到點(diǎn)P的距離了,應(yīng)該設(shè)需要的時(shí)間為xs,這樣AQ=1.5xm,BP=xm,于是有CQ=(15-1.5x)m,CP=(10-x)m.
師:這兩個(gè)數(shù)據(jù)都符合實(shí)際情況嗎?
生:當(dāng)點(diǎn)Q,P在Rt△ACB的邊上時(shí),15-1.5x>0且10-x>0,即0 教學(xué)反思:這個(gè)案例是最初導(dǎo)入情境的變式,盡管情境涵蓋的數(shù)學(xué)關(guān)系式的原理是相同的,但比原來(lái)的問(wèn)題情境有了進(jìn)一步拓展,即不能直接設(shè)定點(diǎn)Q,P走過(guò)的路程了,除非學(xué)生發(fā)現(xiàn)了AB∥QP,這需要獨(dú)到的眼光才能察覺(jué).所以,在用一元二次方程解決實(shí)際問(wèn)題時(shí),假設(shè)的未知量也至關(guān)重要. 總之,用一元二次方程解決實(shí)際問(wèn)題時(shí),問(wèn)題情境的表達(dá)方式是實(shí)際情境的真實(shí)反映.當(dāng)其中有些數(shù)量關(guān)系比較隱蔽時(shí),在探究過(guò)程中假設(shè)未知量以及正確建立一元二次方程是學(xué)生的難點(diǎn),需要教師恰當(dāng)?shù)匾龑?dǎo).在課堂教學(xué)過(guò)程中教師要做到:創(chuàng)設(shè)現(xiàn)實(shí)生活中的實(shí)際問(wèn)題情境,引導(dǎo)學(xué)生進(jìn)入課題;引導(dǎo)探究解題過(guò)程,幫助學(xué)生對(duì)實(shí)際問(wèn)題進(jìn)行數(shù)學(xué)建模;驅(qū)動(dòng)內(nèi)化解題的潛能,強(qiáng)化學(xué)生對(duì)數(shù)學(xué)建模的解題應(yīng)用.這樣,就一定能夠讓學(xué)生弄清問(wèn)題情境,鎖定已知,構(gòu)建聯(lián)系,設(shè)定未知,發(fā)展思維.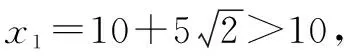
5 結(jié)束語(yǔ)

