幾何最值問題的解題策略
?喀什大學數學與統計學院 陸文昊
1 引言
平面幾何背景下的最值問題,其數學原理可追溯到“兩點之間線段最短”“在直線外一點與直線上各點連接的所有線段中,垂線段最短”“三角形兩邊之和大于第三邊”等幾何學基本定理.蘇教版八年級上冊教科書初次介紹到“將軍飲馬”模型,即利用構造對稱圖形來解決兩條線段和差及其延伸出的多邊形周長最值問題.而我們通常認為的“胡不歸”是以求“PA+kPB”形式的幾何最值出現的,通過垂直構造直角三角形中的三角函數來處理系數k,從而完成思維上的過渡,將問題轉化至求相連兩條線段和的最值.本文將著重圍繞這兩大模型的例題展開剖析,對于更為復雜的最值模型,如“阿氏圓”“費馬點”等,留給學有余力的學生繼續探究,深化對解題原理與解題思路的理解[1].
2 例題解析
2.1 構造直角 轉化系數
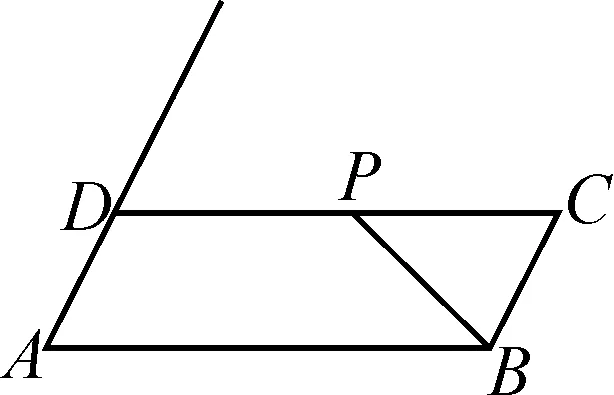
圖1
例1在ABCD中,∠DAB=60°,AB=6,BC=2,P為邊CD上的一動點,則的最小值等于.
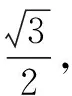
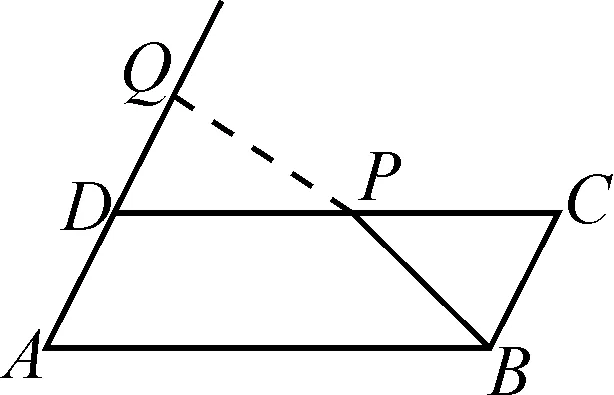
圖2
解析:如圖2所示,過邊CD上的動點P作PQ⊥AD,交AD的延長線于點Q.
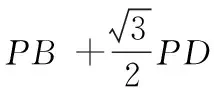
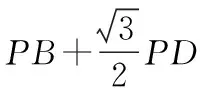
2.2 異端相接 回歸本質
例2如圖3,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中點,直線l經過點D,AE⊥l,BF⊥l,垂足分別為E,F,則AE+BF的最大值為.
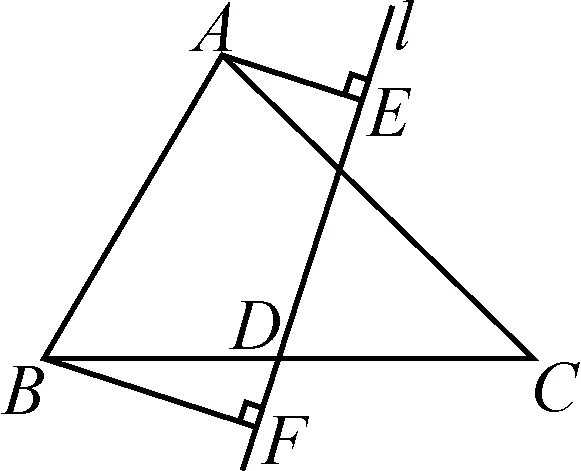
圖3
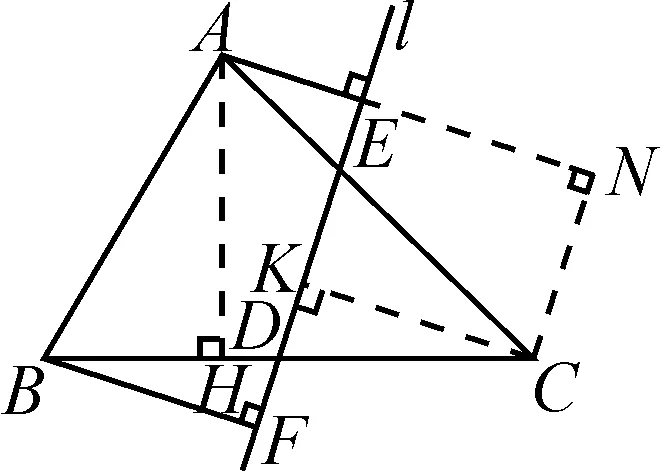
圖4
分析:初看本題,無法再從“胡不歸”模型考慮.但無論從“將軍飲馬”還是“胡不歸”的視角考慮,所求最短路徑之和都由一個公共點相接,而此題的特殊之處在于兩條線段是彼此獨立.如此一來,我們不能將思路限制在兩處的線段本身,而應通過必要的操作,將不常規的問題轉化成熟悉的情形.
解析:充分利用中點D,設法找出與AE相接的BF的等效線段.如圖4,過點C作CK⊥l于點K,過點A作AH⊥BC于點H.
在Rt△AHB中,∠ABC=60°,AB=2,
在Rt△AHC中,∠ACB=45°,
∵點D為BC中點,
∴BD=CD.
在△BFD與△CKD中,
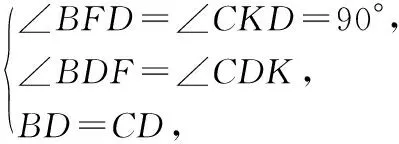
∴△BFD≌△CKD(AAS).
∴BF=CK.
延長AE,過點C作CN⊥AE于點N,可得AE+BF=AE+CK=AE+EN=AN.
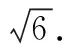
2.3 聚焦目標 化動為靜
例3如圖5,在邊長為4的正方形ABCD中,將△ABD沿射線BD平移,得到△EGF,連接EC,GC.求EC+GC的最小值.
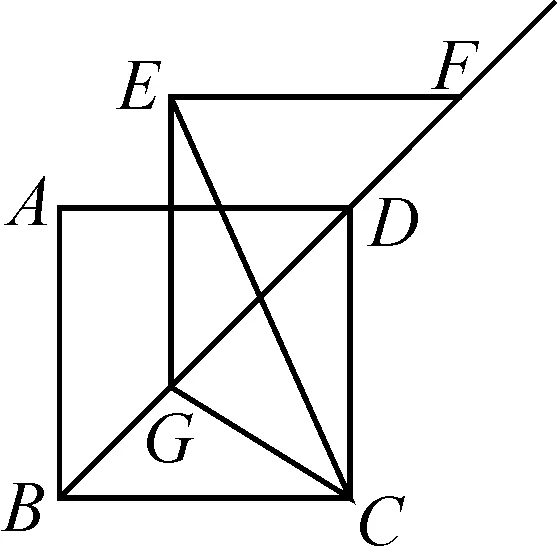
圖5
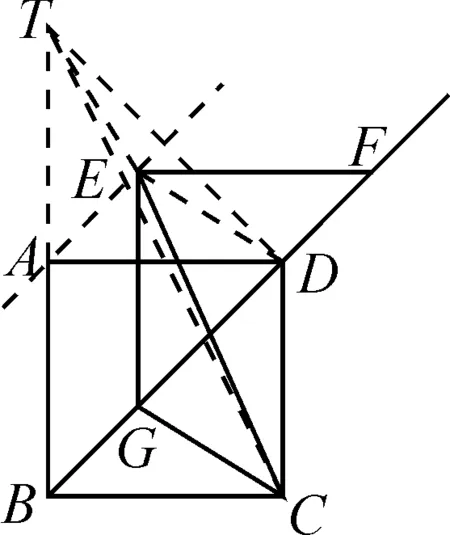
圖6
分析:本題中點E,G始終處在平移的動態中,我們仍需轉化目標.嘗試連結DE,AE,GC長等效到DE處,作點D關于直線AE的對稱點T,這時可以得到“將軍飲馬”的雛形.再連結AT,ET,CT,易證B,A,T共線.
解析:通過上述輔助線的添加,得到圖6.
∵四邊形ABCD是正方形,
∴AB=BC=AD=4,
∠ABC= 90°,∠ABD=45°.
∵AE//BD,
∴∠EAD=∠ABD= 45°.
∵點D,T關于AE對稱,
∴AD=AT=4,∠TAE=∠EAD= 45°.
∴∠TAD=90°.
∵∠BAD= 90°,
∴B,A,T三點共線.
又∵EG=CD,EG//CD,
∴四邊形EGCD是平行四邊形.
∴CG=DE.
∴EC+CG=EC+ED=EC+TE.
∵TE+EC≥TC,
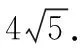
趁熱打鐵,我們來看此類題型的一道拓展:
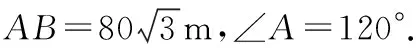
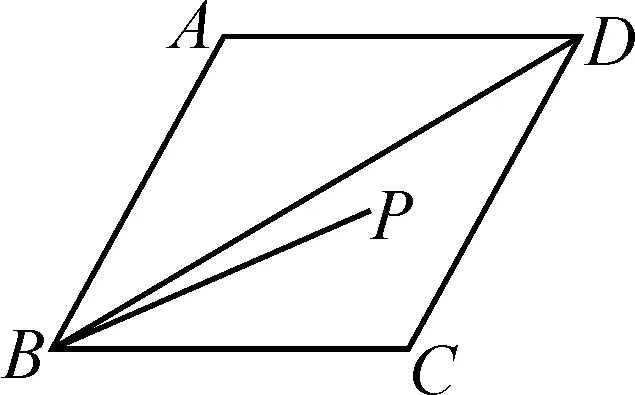
圖7
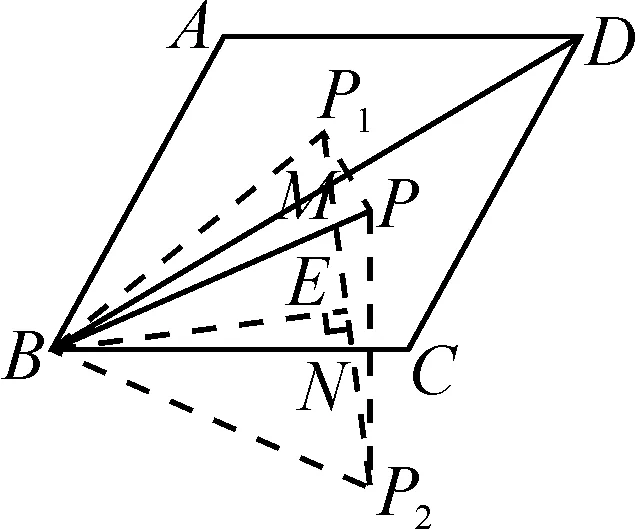
圖8
分析:觀察點P的動態位置,BD,BC是天然存在的對稱軸,作點P關于BD的對稱點P1,關于BC的對應點P2,連接P1P2,分別交BD,BC于點M,N,此時得到△PNM周長最小;而四邊形PMBN的面積問題根據軸對稱的性質、等邊三角形的性質、三角形三邊關系以及外接圓的性質解答即可.
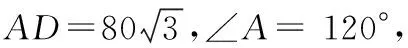
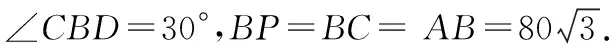
按分析中添輔助線的要求作出△PNM周長最小時的情形,如圖8.
由對稱的性質,可得
BP1=BP=BP2,
∠P1BM=∠PBM,∠P2BN=PBN,
MP1=MP,NP=NP2.
所以∠P1BP2= 2(∠PBM+ ∠PBN)=60°.
因此△P1BP2是等邊三角形,有
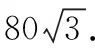
過點B作BE⊥P1P2于點E,則
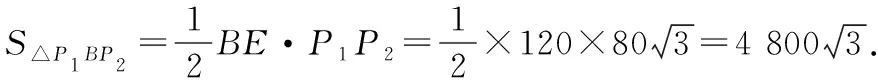
由軸對稱的性質,可得△P1BM≌△PBM,△P2BN≌△PBN.當△BMN的面積最小時,四邊形PMBN的面積最大.
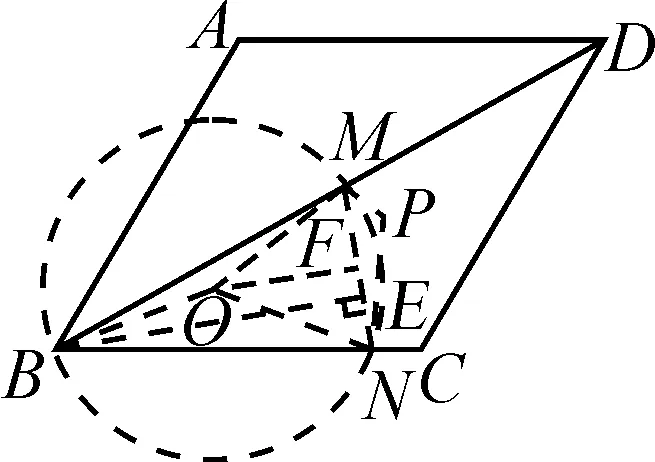
圖9
如圖9,作△BMN的外接圓⊙O,連接OB,OM,ON,過點O作OF⊥MN于點F,∠MON=2∠MBN=60°,所以△MON是等邊三角形.
設⊙O的半徑為R,則
由OB+OF≥BE,得
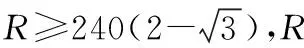
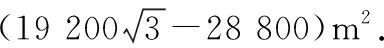
3 結論
通過對以上例題的探討,筆者更希望給予學生幾何最值問題的一種解題思路,在眾多習題的特殊個性中洞悉數學本質的共性.幾何最值問題屬于平面幾何的綜合應用,除了將基本模型轉化以外,主要還會結合三角形的性質、四邊形的性質、解直角三角形、軸對稱的性質、圓的性質等知識點,靈活應用先前建構起來的基礎知識與基本技能完成解答[2].在“將軍飲馬”的動態過程中尋求不變與等效的量,在“胡不歸”處理系數的選擇上提高數感,均為提高解題能力之關鍵.

