培養學生“抽象理解能力”的分析

?江蘇省張家港市南沙中學 蔣 蕾

1 引言

數學是一門非常抽象的基礎性學科，來源于生活，研究數量關系和空間形式，通過抽象體現數學之美.初中是培養學生數學核心素養的重要階段，初中數學學習能夠培養學生“抽象理解能力”，幫助學生更好地掌握和理解變量、函數等基本數學概念，同時也需要學生具備一定的抽象思維，能夠運用所學的數學概念進行推斷.但在實際教學中，許多初中生仍舊以形象思維為主，抽象理解能力比較薄弱，在學習一些抽象化程度較高的數學知識時，理解上有一定難度.因此，教師要多方面、多途徑、多維度加強學生抽象理解能力的培養.

2 “抽象理解能力”的作用

在初中數學教學中，數學教材涉及大量的數學抽象概念，數學概念是數學學科的重要組成部分，也是數學學習的基礎.教師通過引導學生學習數學相關概念，幫助學生學會分析、判斷各種問題，在長期的學習過程中形成抽象理解能力和整合能力，對學生產生良好的指導作用.抽象理解能力對學生數學學科的學習極其重要，能夠讓學生充分了解所研究事物的本質屬性，并進行精確的提煉.在初中數學教材中，許多數學理論都是通過分析、比較多種事物的屬性，由一定的抽象方式形成的.因此，學生擁有抽象理解能力就能夠更好地理解和掌握各種概念.

3 培養學生“抽象理解能力”的具體措施

3.1 通過形成數學概念和規則

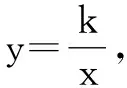
學生對數學概念有一定的理解后，教師要積極引導學生應用理論知識解決實際問題，以此實現抽象概念的具體化分析，促進學生抽象理解能力的提升.此外，教師要注意引導學生發現數學概念間的聯系，從中尋找、分析相應的數學規則，進而逐步構建數學概念理論體系，強調數學知識的整體性，以促進學生主動思考、探索，提升學生的抽象理解能力.

3.2 通過形成數學思想和方法

初中數學教材中涉及多種數學思想和方法，比如：分類討論思想、轉化思想、函數與方程思想等.教師可通過幫助學生形成數學思想，促進學生抽象理解能力的提升.在教學過程中，教師要結合具體內容，適時進行數學思想和方法的滲透.在學習不同章節時，及時向學生介紹不同數學思想與方法，并引導學生探索其內涵.此外，遇到難度較高的綜合性問題時，教師可引導學生運用合適的數學思想與方法分析、探究問題，以尋求解決問題的思路，得到答案.在引導學生學習數學知識時，教師可結合實際情況設計探究性問題，幫助學生利用數學思想與方法進行分析、探究.例如：小童的奶奶步行去社區衛生服務中心做理療，從家走了15min到達距離家900m的社區衛生服務中心，她用了20min做理療，然后用10min原路返回家中，請畫出小童的奶奶離家的距離s(單位：m)與時間t(單位：min)之間的函數關系圖象.本題是比較典型的結合實際的題目，學生可利用一次函數的相關知識分析兩變量之間的函數關系，列出各時間段的函數解析式，最后運用數形結合思想畫出距離與時間之間的函數圖象.在解題過程中，學生要綜合分析、抽象已知條件，靈活地將實際問題轉化為函數模型，幫助學生在應用中領悟數學思想，增強學生的應用意識、創新意識和抽象意識.

3.3 通過形成數學結構和體系

任何事物都擁有特定的結構，不同的結構代表不同的性質.數學以抽象知識為主，具有完整的理論結構，數學結構和體系涉及到許多分支，以及大量數學概念、原理.在初中數學課堂教學中，教師要引導學生全面掌握數學課程結構特征，并逐步構建出完善的數學結構和體系.在實際課堂中，教師要根據數學教學目標設計合理的教學方案，通過數學課堂教學，引導學生逐漸掌握數學結構和體系，建立數學知識框架，進而引導學生自主探索問題，了解并掌握數學新概念和新原理，從而培養學生抽象理解能力.學生可對各章節知識點、概念、原理等進行綜合分析，以此掌握不同知識點與原理之間的內在聯系，站在總體角度，將兩者聯系起來，并組成一個有機整體.

3.4 通過鼓勵學生在協作中運用逆向思維

數學課程的主要任務是理解數學的意義，理解數的標志.數學課堂中，學生通過小組學習與交流，充分發揮各自的優勢，取人之長，補己之短，提升合作交流能力和抽象理解能力.逆向思維有利于學生更好地理解數學問題，學生可通過正反兩方面解決思維障礙、攻克難題，例如，在小組合作討論問題時，可進行小組分工，比較不同解題方式的快慢，激發學生的抽象思維能力.

3.5 注重直觀教學

數學是一門抽象性學科，但是許多抽象的數學概念和數學原理都源于直觀的生活，所以教師在講解復雜深奧的數學知識時應該合理地化抽象為直觀，幫助學生更好地理解抽象知識，有利于培養學生的抽象理解能力.數學抽象與數學直觀是相互促進、相互依存的，因此，教師可利用生動的直觀教學幫助學生培養數學抽象思維，通過多媒體技術和各種輔助教學道具調動學生各感官，幫助學生從直觀的學習中理解抽象的數學概念和數學原理，提升學生抽象思維能力，有利于學生更透徹地掌握數學知識，從而提升教學質量，提高數學課堂效率.例如，在講解九年級上冊第二章第5節的“直線和圓的位置關系”(蘇科版)時，教師先利用課件展示一組“海上日出”的圖片，感受生活中反映直線與圓的位置關系的情境：在太陽升起的過程中，如果把太陽看作一個圓，把地平線看作一條直線，那么直線與圓的位置關系可以表示為三種(出示三幅圖).接著讓學生在練習本上畫一個圓，把直尺當作直線，移動直尺，觀察直線和圓的位置，教師用《幾何畫板》演示直線和圓的相對運動，讓學生感受直線與圓的位置關系的變化.通過直線與圓的公共點的個數以及圓心到直線的距離的變化和相關關系，歸納得出直線和圓的三種位置關系，了解直線與圓相交、相切、相離的概念.借助直觀教學向學生進一步講解直線與圓的位置關系的性質與判斷.

4 結束語

在初中數學教學過程中，培養學生的抽象理解能力是十分重要的.對教師而言，培養學生抽象思維是一個系統的過程，需要多方面積極引導學生逐步掌握數學概念、數學思想方法、數學結構體系，促進學生深化理解數學原理和數學概念，領悟抽象數學知識和實際生活的聯系，提升學生的數學素養和創新理解能力.