圖正則重加權稀疏約束的深度非負矩陣分解算法用于高光譜圖像解混

蔣永叢， 何 飛

(1. 河南林業職業學院信息與藝術設計系，河南 洛陽 471002; 2. 鄭州大學信息工程學院，河南 鄭州 450001)

0 引 言

高光譜圖像作為對地遙感觀測的一種重要手段，在服務國防科技、農業發展、水資源監測、環境災害等方面發揮著不可替代的作用[1-3]。但受限于有限的空間分辨率，高光譜圖像中容易出現混合像元，即一個圖像像元光譜是由一個或幾個地物光譜混合而成[4-5]。高光譜解混是一種將圖像混合像元分解成一組最純的端元光譜和其對應的組成豐度的技術[6]。高光譜解混是解譯高光譜圖像的一種重要途徑，因此對高光譜解混算法的研究變得格外重要。

當前高光譜圖像混合像元分解算法可以大致分為三類。第一類是無監督解混算法，這一類算法從圖像中提取指定數目端元，然后再采用全約束最小二乘算法估計端元對應的豐度。典型的算法包括頂點成分分析法（vertex component analysis, VCA ）[7]，空間能量約束的最大單純形體積法（spatial energy prior constrained maximum simplex volume,SENMAV）[8]，空間單純形加權端元提取法（spatially weighted simplex strategy，SWSS）[9]。第二類算法是有監督解混算法，這一類算法采用一個完備的光譜庫作為字典，不對圖像進行端元提取，僅需要估計圖像混合像元的豐度成分。典型算法包括空譜加權稀 疏 回 歸 法 （ spectral-spatial weighted sparse regression，SSWSR）[10]，光譜多視角協同稀疏回歸法（spectral multiview collaborative sparse unmixing,SMCSU）[11]。第三類算法是基于非負矩陣分解（nonnegative matrix factorization, NMF）模型的無監督解混算法。這一類算法將高光譜圖像分解成兩個非負矩陣，即端元矩陣和豐度矩陣。由于NMF模型是非凸的，難以獲得全局最小值。因此通常采用針對端元或豐度的先驗知識來對模型施以約束以提升模型的求解精度。典型的基于NMF模型的解混算法包括有L1/2稀疏約束的NMF（L1/2constrained NMF, L1/2-NMF）[12]， 空 間 組 稀 疏 約 束 的 NMF（spatial group sparsity constrained NMF, SGS-NMF）[13]。

當前，在圖像處理的研究過程中，深度學習范式越來越受到研究人員的關注，因為深度學習相比傳統算法而言更加關注數據的隱層結構。為了使NMF算法也能獲得學習隱層信息的能力，有研究人員提出了深度NMF算法，這類算法通過將端元矩陣經過多層分解以挖掘圖像的深度信息。典型算法包括有多層非負矩陣分解算法（multi-layer NMF,MLNMF）[14]，稀疏深度非負矩陣分解算法（sparse deep NMF, SD-NMF）[15]。但這類算法仍然存在典型問題，即在深度分解的過程中無法有效地挖掘圖像的先驗信息以提升解混性能。

為了有效提升高光譜圖像解混性能，提出了一種圖正則和重加權稀疏約束的多層深度非負矩陣分解 算 法 （ graph regularized and reweighted sparsity constrained deep nonnegative matrix factorization,GRS-DNMF）。提出的 GRS-DNMF對傳統 NMF模型分解得到的端元矩陣進行多層分解直至到達指定層數，并對各層中豐度矩陣同時施加圖和稀疏約束以提升模型的魯棒性。模擬數據集和真實數據集實驗驗證了所提出的GRS-DNMF算法相比其他算法具有明顯解混優勢。本文GRS-DNMF算法的核心創新點在于提出了一種對非負矩陣分解進行多層分解的深度模型且利用同時利用稀疏和圖約束對多層豐度矩陣進行正則的方法。

1 光譜線性混合模型與非負矩陣分解算法

高光譜圖像像元混合模型通常假定滿足光譜的線性混合，表述如下：

式中： Y ∈ RB×N——包含個波段和個像元的高光譜圖像；

M ∈RB×K——包含個光譜的端元矩陣；

A∈RK×N——個光譜的端元所對應的豐度矩陣；

E∈RB×N——噪聲矩陣。

需要指出的是，線性混合模型通常需要滿足兩個本質約束項即豐度非負約束和豐度和為一約束。

非負矩陣分解算法是一種將多信號混合的數據分解成兩個非負矩陣的乘積的一種有效方式。NMF通常表述如下的形式：

通過讓上式分別對兩個非負矩陣進行最小化優化，NMF算法可以有效求解兩個非負矩陣，目標函數表述如下：

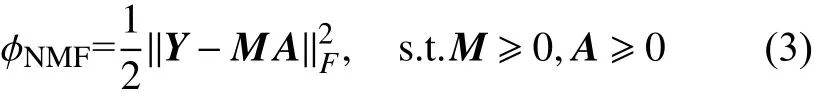
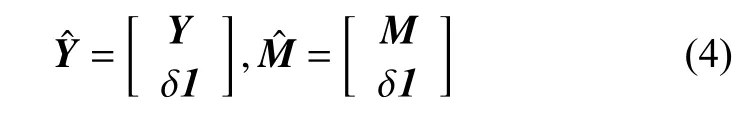
2 提出的圖正則重加權稀疏多層深度非負矩陣分解算法

2.1 模型提出

為了有效提升NMF算法對高光譜圖像的解混性能，提出了一種基于圖正則和重加權稀疏約束的多層深度非負矩陣算法GRS-DNMF。對于多層深度非負矩陣算法，其第一層是將進行常規分解，形成和。第二層中，將第一層中的繼續分解成和。這個過程將會重復繼續下去，直至到達指定的層。對于多層深度非負矩陣模型，其最終的多層結構表述如下

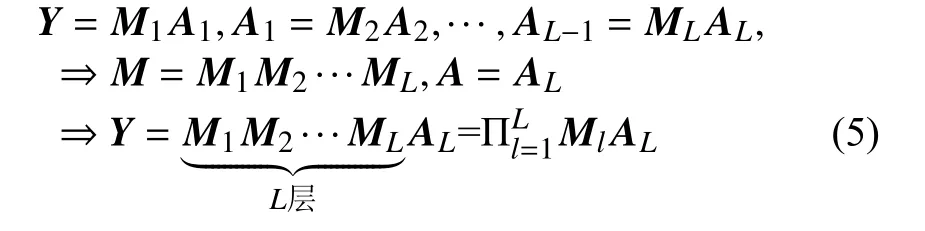
對于第l層，多層深度非負矩陣分解模塊在該層的模型可以表述如下

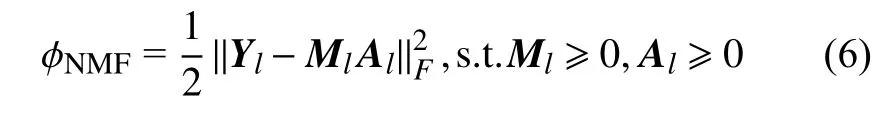
為了有效提升模型的魯棒性，增強對高光譜圖像的分解能力，本文采用圖結構和重加權稀疏正則項對模型施以約束。為了有效挖掘圖像和豐度矩陣在局部所具有的本質特征，即圖像局部數據是空間光譜相似的，其豐度成分也應該是相近的。因此，通過獲取圖像局部數據的圖結構并讓其在豐度矩陣局部保持同樣結構能有效提升豐度矩陣的估計效果。另一方面，豐度矩陣通常是表征圖像中少量端元在混合像元時的成分。但事實上，對于混合像元而言，其通常由少量光譜混合而成，因此豐度矩陣呈現稀疏性。通常研究人員采用或稀疏項，但并沒有稀疏，而相比是非凸的。為了避免和的問題，本文采用重加權稀疏正則項，通過引入權重矩陣來增強迭代優化過程中豐度矩陣的稀疏性。重加權同時具有的稀疏度和的凸結構。通過融合圖結構和重加權稀疏正則項，在第l層的模型可以表述為

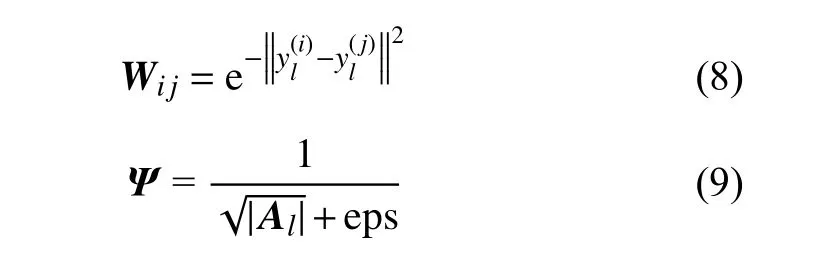
2.2 模型優化

為了方便模型的優化，首先將圖正則約束項作如下改寫：

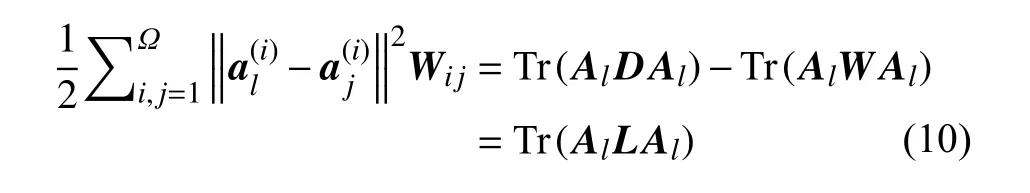
L=D-W——圖拉普拉斯矩陣。

因此原始模型可以重新表述如下：

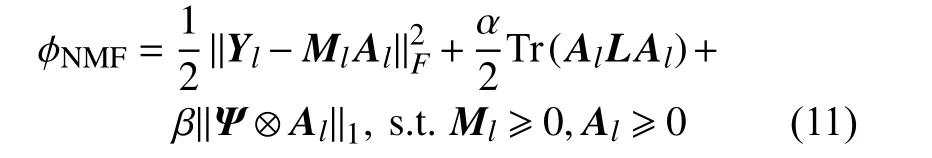
將非負和和為一約束寫入模型，則拉格朗日函數可以表述如下

2.3 算法偽代碼

為了有效闡述所提出的算法的求解流程，本文提供了算法的標準偽代碼。偽代碼如下所示：

3 實驗結果與分析

3.1 實驗評價方法

為了有效驗證所提出的算法和對比算法在不同數據集上的有效性，本文采用兩種典型的度量方法，即光譜角距離（spectral angle distance, SAD）和均方根誤差（Root Mean Error Square）。SAD 度量原始光譜和從圖像中估計出的光譜之間的光譜相似度，SAD值越低，表明兩個光譜相關性高。和之間的SAD表述如下：

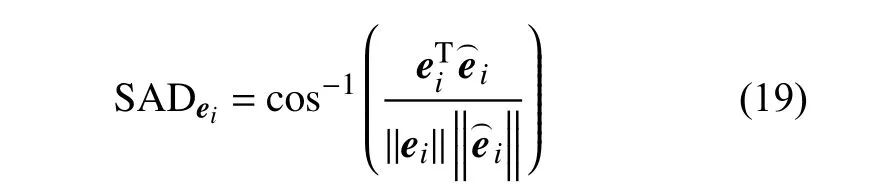
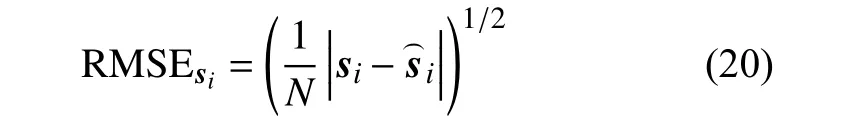
3.2 實驗數據集

為了有效驗證不同算法在不同場景數據集下的解混性能，本文采用兩種數據集包括一種模擬數據集和一種真實數據集。模擬數據集由6種包含有224個波段的光譜按照一定比例混合而成。為了更好模擬真實的圖像場景，不同信噪比(signal-tonoise ratio, SNR)的零均值高斯白噪聲將會添加在模擬圖像中，且豐度矩陣中像元最高的光譜純度為0.8即圖像中并不包含純像元。模擬圖像如圖1所示。

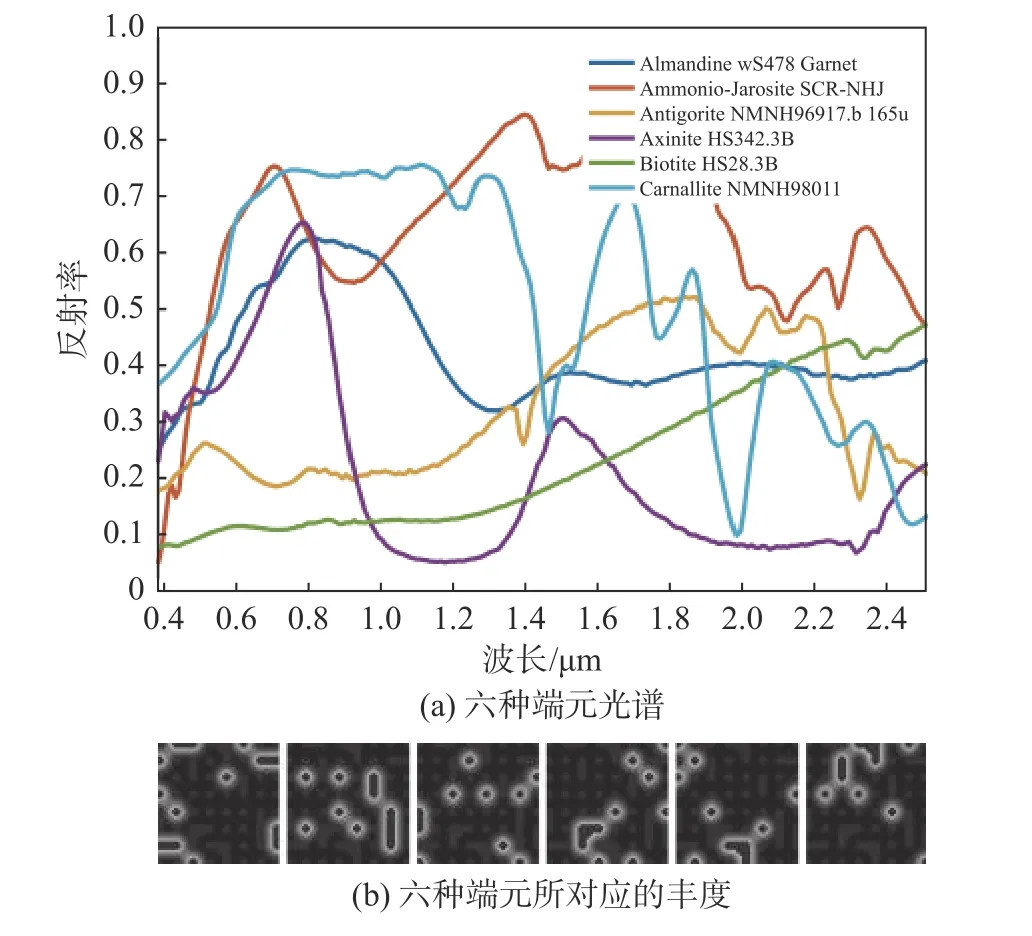
圖1 模擬數據集

真實數據集采用高光譜解混標準數據集Cuprite，該數據集由機載紅外成像光譜儀在美國內華達州Las Vegas地區拍攝。原Cuprite數據集尺度包含224個波段，考慮到水汽和噪聲干擾，移除第1～6、105～115、150～170和 221～224波段，保留 182個波段。圖像采用250×190×182大小的子圖像作為實驗數據集。采用端元數目估測算法對Cuprite數據集進行估測的端元數目為12。Cuprite數據集偽彩色圖像如圖2所示。

圖2 Cuprite數據集偽彩色圖像

3.3 對比算法與參數選擇

為了有效驗證所提出GRS-DNMF算法的有效性，采用3種標準算法進行實驗對比，分別為端元提取算法VCA，L1/2-NMF算法和MLNMF算法。對于VCA算法，其是一種典型的無監督算法，僅需要輸入圖像矩陣和指定端元數目。對于L1/2-NMF算法，正則參數可以通過度量圖像的稀疏度來確定。對于MLNMF算法，其涉及到對端元矩陣和豐度矩陣的稀疏約束和深度層的數目，這些參數分別設置為 3×10-5，7×10-5，10。

本文所提出的GRS-DNMF算法涉及到豐度的圖和稀疏正則項以及深度層的參數。為了驗證不同參數對模型解混精度的影響，分別將分別從1×10-5變化到 5×10-1，從 1×10-4變化到 5×10-1，層數 l 從1變化到10。如圖3～圖5所示，當，和層數 l分別設置為1×10-1，1×10-2，3 時 GRS-DNMF能產生最優解混結果。

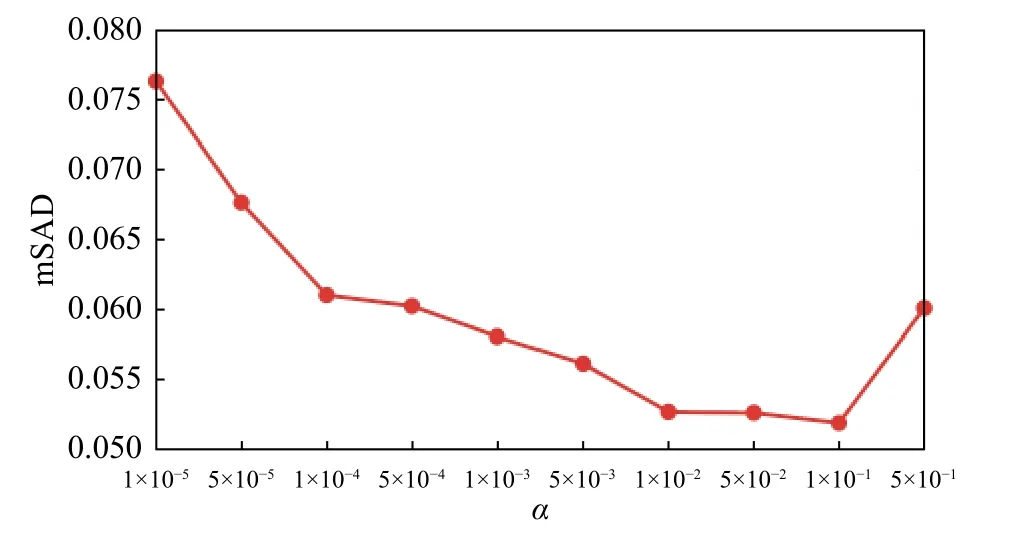
圖3 GRS-DNMF算法在不同的平均SAD值

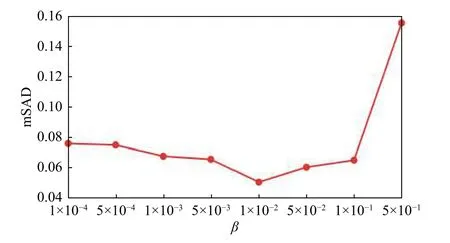
圖4 GRS-DNMF算法在不同的平均SAD值

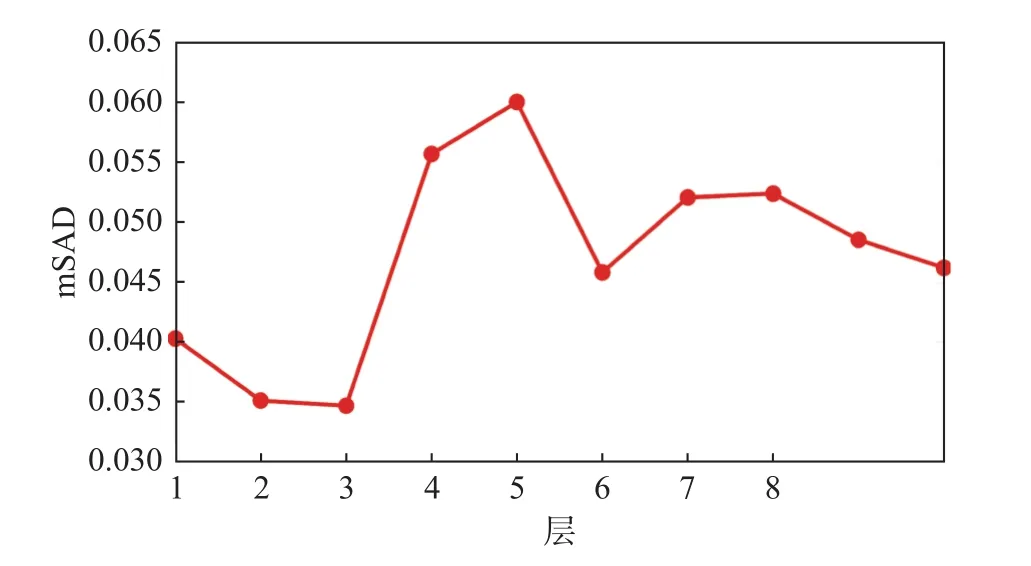
圖5 GRS-DNMF算法在不同層的平均SAD值

3.4 噪聲水平對算法解混精度的影響

為了度量所提出的算法和三種標準對比算法在不同信噪比情況下的端元提取精度，本試驗對模擬數據分別添加15 dB至45 dB的零均值高斯噪聲。圖6展現了四種算法在不同信噪比下的端元提取平均SAD的變化趨勢。如圖所示，隨著噪聲的減弱，所有算法能逐漸獲得較好的端元提取性能。但相比其他算法，本文所提出的算法無論是在噪聲強度大的情況下還是在弱噪聲的情況下均能獲得最優的端元提取精度。

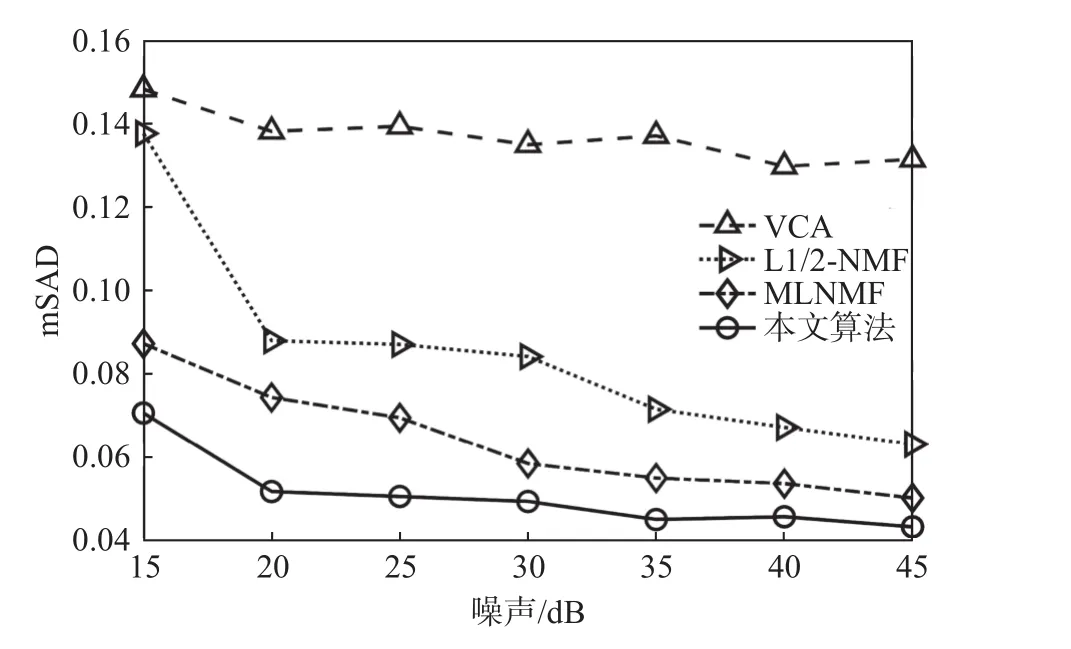
圖6 四種算法在不同SNR下的平均SAD值

3.5 不同算法對圖像的解混性能評價

為了度量所提出的算法和三種標準算法在模擬數據下提取端元的精度，本文考慮了在30 dB噪聲的模擬數據下的算法性能對比。表1展現了四種算法在包含了6種端元的模擬數據集下的端元提取精度。從表中可以看出，對于6種端元，所提出的算法能準確地對其中三種端元進行估計并且能提供最小的平均SAD值，而MLNMF和L1/2-NMF算法則分別能提供對另外兩個和一個光譜的準確度量。表2展現了四種算法在模擬數據集上對6種端元所對應的豐度進行估計的結果。與表1所呈現的結果類似，對于三種端元所對應的豐度而言，其依然能提供最優的豐度估計結果以及最小的平均RMSE值。實驗證明所提出的算法相比其他算法在高光譜解混的任務中，能提供更優異的解混精度。

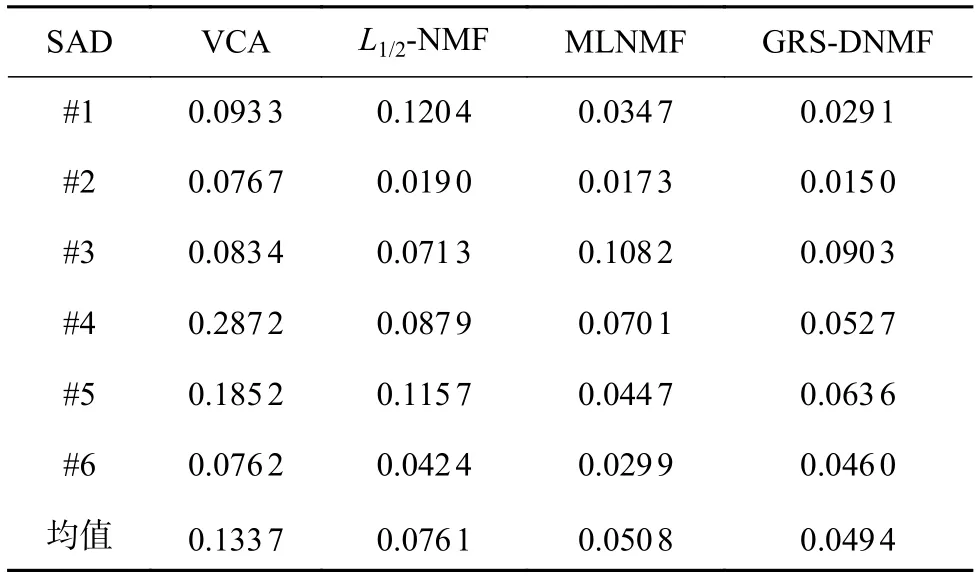
表1 不同算法提取6種光譜的SAD值和平均SAD值

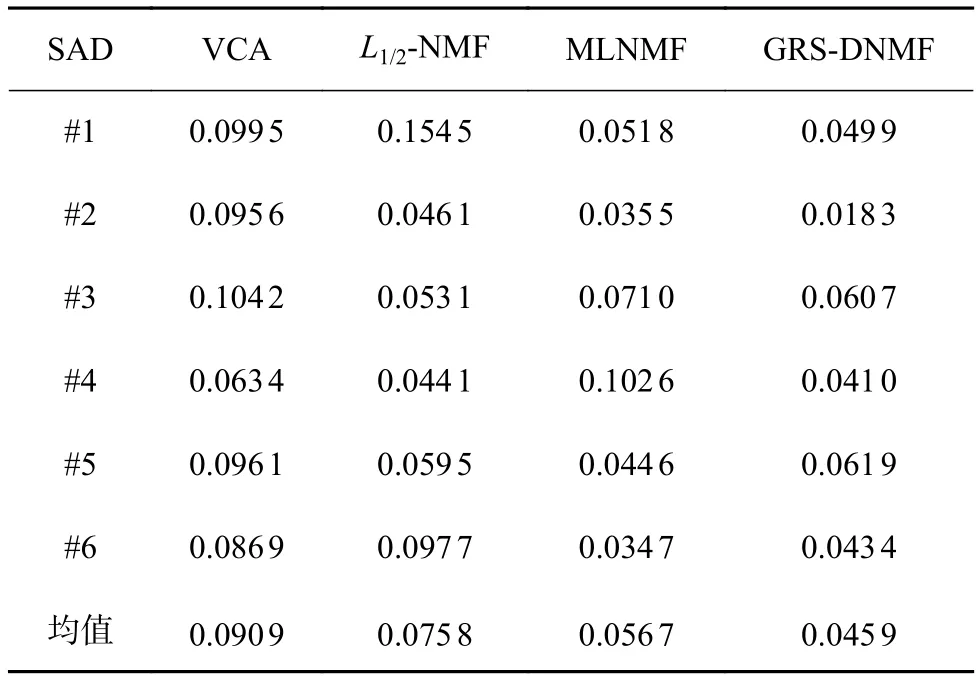
表2 不同算法提取6種光譜的RMSE值和平均RMSE值

3.6 算法解混效果的可視化評價

為了可視化地展現所提出的算法在30 dB噪聲下進行解混任務后的光譜曲線，圖7展現了6幅由算法提取的光譜和真實光譜可視化對比的圖像。由圖7可以觀測出，對于真實光譜而言，由算法所提取的光譜具有較好的擬合效果。同時，為了可視化展現算法在不同噪聲情況下估計的豐度和真實豐度之間的差異性，算法在 15 dB、25 dB、35 dB、45 dB噪聲的模擬數據下進行了解混任務并進行豐度對比。圖8展現了豐度對比圖，相比真實豐度，在高噪聲的情況下，算法所估計的豐度雖然能較好地恢復出真實豐度但一定程度上仍然受噪聲的影響，如在15 dB情況下。但在噪聲略微減弱的情況下，如25 dB到45 dB，算法則能完整恢復出真實豐度。

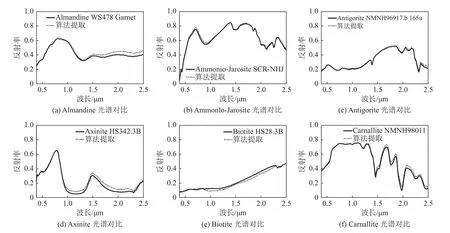
圖7 GRS-NMF 算法提取的 6 種端元（點劃線）和真實端元（實線）的可視化對比

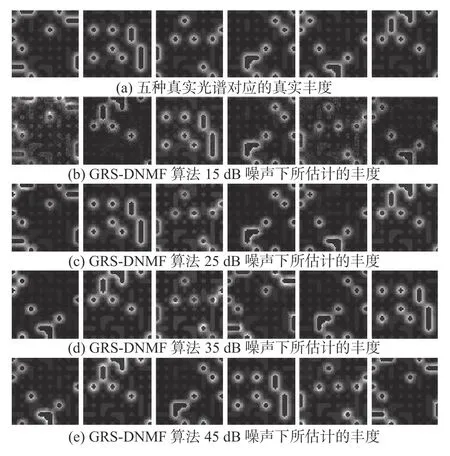
圖8 GRS-NMF 算法在不同噪聲下估計的豐度和真實豐度的可視化對比

3.7 不同算法在真實數據集上的解混效果

本試驗是為了衡量不同算法在地物混合更加復雜的Cuprite數據集下的解混精度。表3展現了4種算法提取12種地物的SAD數值。如表3所示，在更為復雜的Cuprite數據集下，所提出的算法依然能準確地估計出5種地物的光譜，緊接著的是L1/2-NMF算法，其能對4種地物光譜進行估計，而MLNMF和VCA則分別能獲得2種地物和1種地物的最優光譜估計性能。此外，所提出的算法對于12種地物能獲得最低的平均SAD值，這證明了該算法具有較強的魯棒性。圖9可視化地展現了提取的12種光譜和光譜庫之間的對比。由圖可知，由算法提取出的光譜基本上匹配了標準光譜庫光譜。此外，圖10展現了算法分解出的12種礦物所對應的豐度。

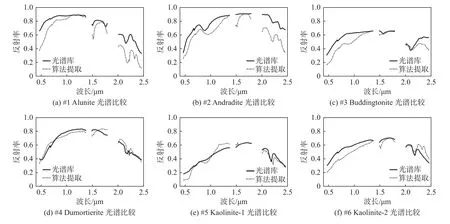
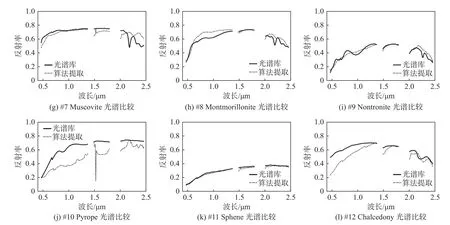
圖9 GRS-NMF 算法在 Cuprite 數據集上提取的 12 種端元（點劃線）和真實端元（實線）的可視化對比

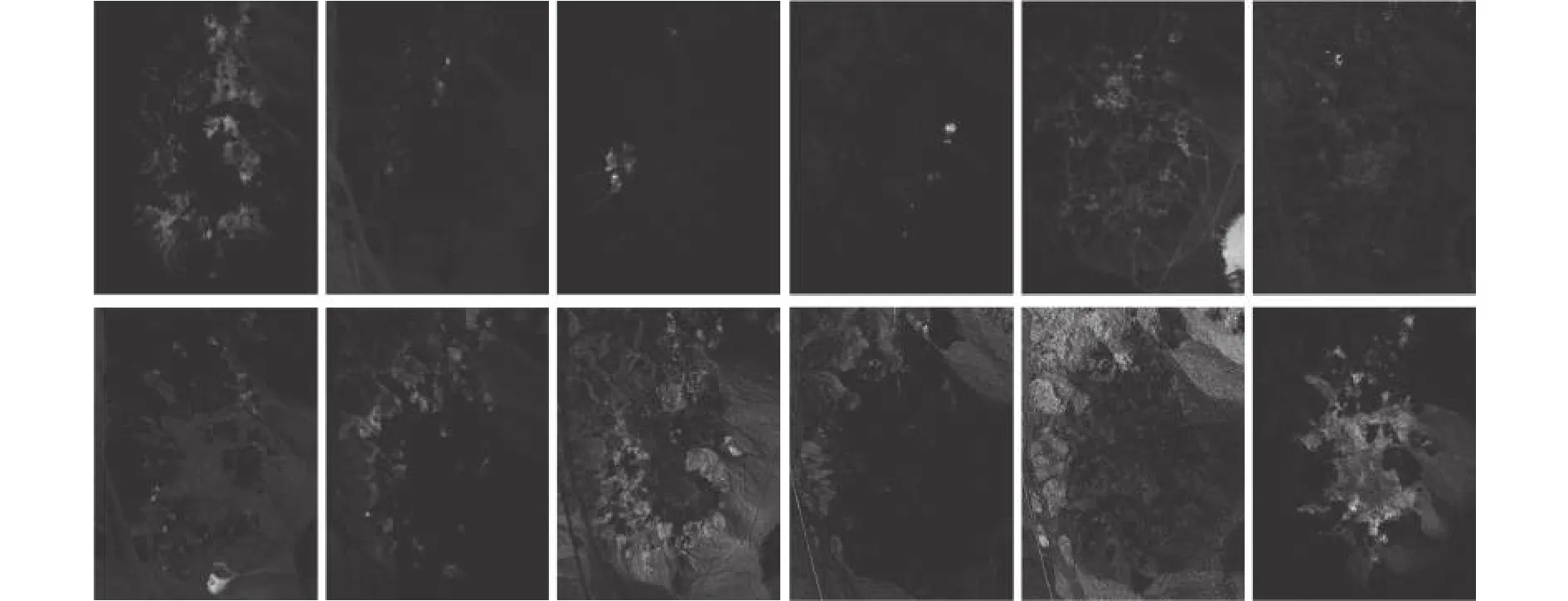
圖10 GRS-NMF算法在Cuprite數據集提取的12種豐度的可視化展示

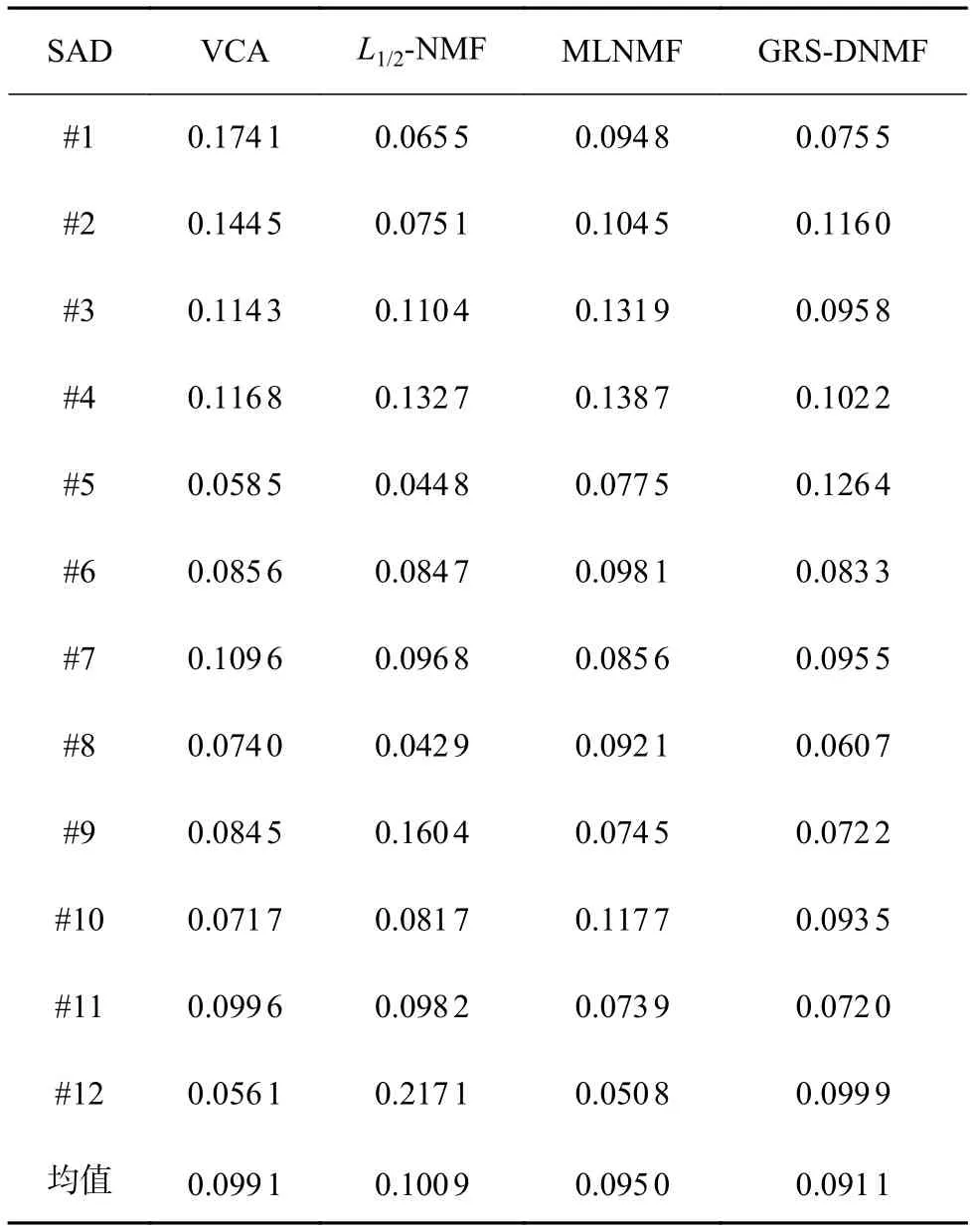
表3 不同算法提取6種光譜的SAD值

4 結束語

為了有效提升目前高光譜解混算法對高光譜圖像解譯的水平，提出了一種圖和重加權稀疏正則的多層深度非負矩陣分解算法。該算法對端元矩陣進行多層的分解并對相對應的豐度矩陣施加圖和稀疏約束直至分解至指定層數。在模擬數據和真實數據上的解混實驗對比中，所提出的算法相比其他算法具有更明顯的魯棒性且能有效提升高光譜圖像的解混能力。實驗證明，所提出的算法在未來可以有效應用于國防科技領域，成為一種有效的對地觀測手段。