鋼筋混凝土歷史建筑中方鋼-混凝土的極限粘結應力分析

糜鎮東，淳慶，金輝

(東南大學 建筑學院，江蘇 南京 210008)

近代時期，鋼筋混凝土結構技術由西方傳入中國并大量應用于各大城市建設中.目前，保留下來的鋼筋混凝土歷史建筑大量存在于北京、上海、武漢、天津、青島、西安、廈門、廣州、濟南、南京、杭州等大中型城市中.這些鋼筋混凝土歷史建筑是中國城鎮建筑遺產的重要組成部分，具有重要的歷史價值、藝術價值、科學價值和社會價值.而近代鋼筋混凝土建筑中使用最為廣泛的方鋼在形狀與構造方面明顯不同于現代圓鋼，因而其粘結滑移性能與現代圓鋼也有明顯不同.

粘結滑移性能是評判鋼筋混凝土結構的承載性能和變形性能的重要指標[1].現代圓形鋼筋與混凝土之間的粘結滑移關系主要通過拉拔實驗、梁式實驗與軸拉實驗3種實驗方式進行研究.Lutz等[2]通過鋼筋與混凝土的拉拔實驗，提出鋼筋與混凝土之間的粘結力主要由化學結合力、摩擦力與機械咬合力3個部分組成.國內外學者大量研究表明，鋼筋的直徑、肋間距、肋的形狀對粘結應力有決定性作用，且肋的形狀決定了裂縫大小和最終的破壞模式[3-5].另外，混凝土的抗拉強度和鋼筋的屈服強度也是鋼筋混凝土極限粘結應力的重要影響因子[6-7].

上世紀60年代至今，國內外學者提出了大量現代圓形鋼筋與混凝土的粘結滑移理論模型.早在1977年，Orangun等[8]就通過實驗得出帶箍筋的鋼筋混凝土粘結應力的表達式；Darwin等[9-10]擬合了帶箍筋和不帶箍筋的鋼筋混凝土粘結應力表達式并進行驗證；在此基礎上，Harajli[11-12]對高強混凝土、普通混凝土等劈裂破壞形式的粘結滑移公式進行推導.目前僅有少數關于近代方鋼-混凝土粘結性能的試驗研究.張時琦[13]對近代方鋼進行拉拔實驗，根據現代的混凝土規范，擬合粘結應力四段折線圖，并且根據該本構模型對近代鋼筋混凝土梁進行ANSYS有限元模擬分析.Chun等[14]搜集整理了近代民國關于鋼筋混凝土規范的資料，并對近代鋼筋進行本構關系的實驗研究，得出近代鋼筋的本構模型，總結近代鋼筋的大致尺寸形制，研究近代時期常用的方鋼、螺旋鋼、扁截鋼的力學特性.

綜上所述，目前關于鋼筋混凝土的粘結滑移性能研究主要針對現代圓鋼，而關于近代方鋼-混凝土粘結滑移計算模型的研究鮮有報道.因此，本文對近代鋼筋混凝土結構中的方鋼-混凝土極限粘結應力的計算模型進行研究.

1 近代文獻關于方鋼-混凝土的粘結性能規定

近代文獻規定的方鋼-混凝土極限粘結應力的安全值[15-27]，如表1所示.表1中：τ為方鋼-混凝土的極限粘結應力；fcu，fct分別為混凝土的抗壓強度和抗拉強度；fc，28 d為混凝土養護28 d后抗壓強度；ftr為混凝土的抗拉強度設計值.近代時期，國內工程界對混凝土配比的使用較為單一，大多混凝土配比為V(水泥)∶V(砂子)∶V(石子)=1∶2∶4，V為體積，《鋼筋混凝土學》[24]規定濕拌法的混凝土用水量(質量)為干料總質量的10%～13%.因此，近代時期的混凝土抗壓強度相對固定，澆筑28 d后的抗壓強度為14.00～16.46 MPa；而混凝土的設計值通常取安全系數為3～5，較為保守[24].

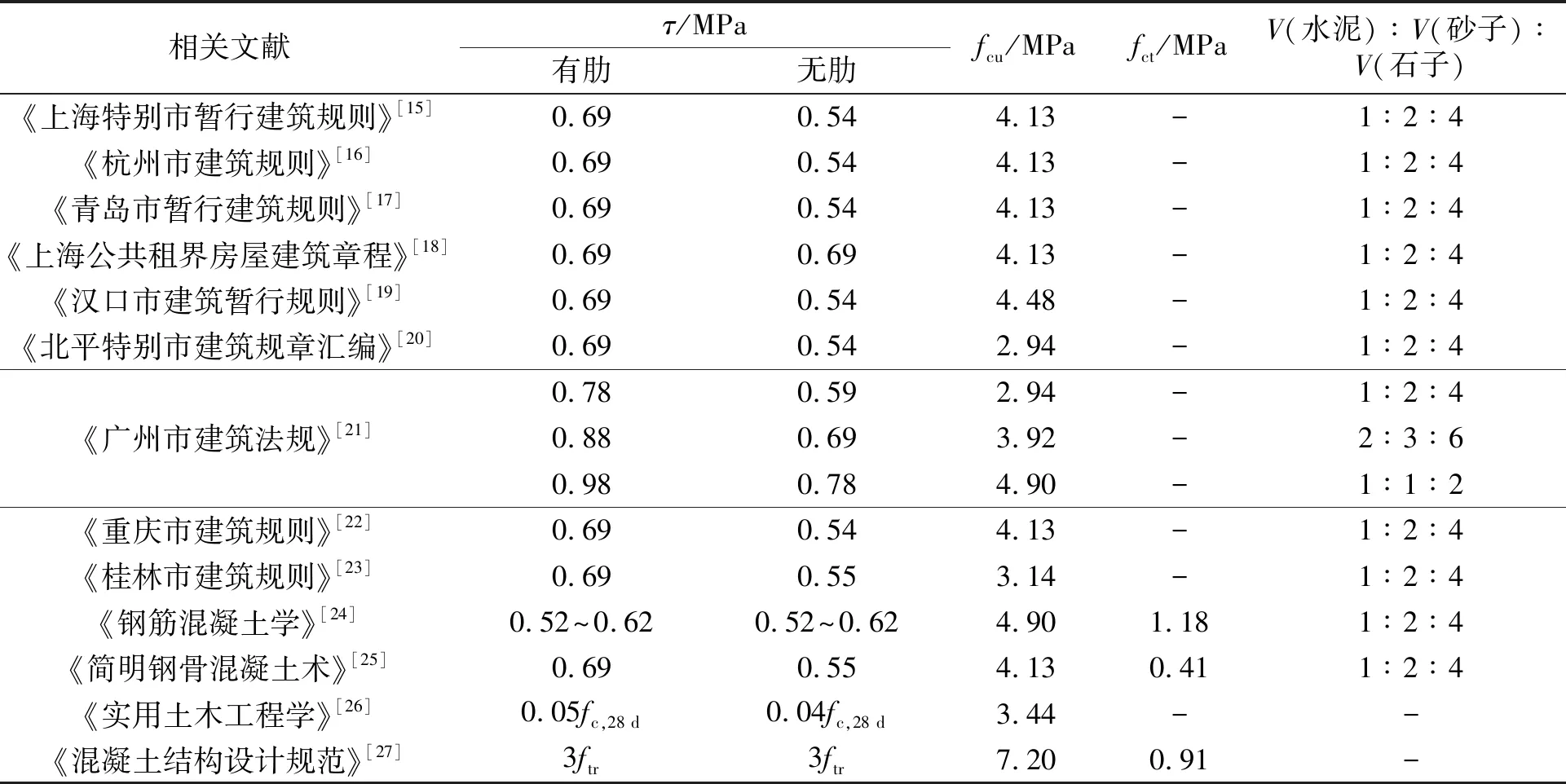
表1 近代文獻規定的方鋼-混凝土粘結應力的安全值Tab.1 Safety values of bond stress of square rebar-concrete regulated in modern literatures

近代中國工程界明確了方鋼-混凝土之間的粘結力主要由混凝土對鋼筋握裹作用產生的摩擦阻力和方鋼表面粗糙不平的機械咬合力組成；方鋼-混凝土粘結滑移極限應力安全值約為0.5～0.8 MPa，當混凝土中的水泥體積比小于常用配比(V(水泥)∶V(砂子)∶V(石子)=1∶2∶4)時，應該對安全粘結力進行酌減，當水泥體積比大于常用比例時，可對安全粘結力進行酌增[16-17，19-20，23].

參考文獻[28]，結合課題組完成的數十個近代方鋼-混凝土建筑的檢測評估結果，可以認為近代混凝土強度等級為C15.依據GB 50010-2010《混凝土結構設計規范》[27]，近代混凝土軸心抗壓強度標準值為10 MPa，其抗拉強度標準值ftk為1.27 MPa，軸心抗拉強度特征值ftr為0.91 MPa，因此，近代方鋼-混凝土的極限粘結應力設計值應為2.73 MPa.由此可見，近代時期雖對方鋼-混凝土間的粘結滑移性能有一定的認識，但其設計強度過于保守，近代方鋼-混凝土極限粘結應力的設計安全值約為現行規范下設計值的0.19～0.29倍.

2 方鋼-混凝土粘結性能的理論模型

目前，鋼筋混凝土粘結性能的理論模型均是針對圓形截面的鋼筋類型，不適用于方鋼-混凝土的粘結性能分析.因此，基于近代方鋼的構造特征，推導近代方鋼-混凝土的粘結性能理論計算模型.

方鋼形狀簡化圖，如圖1所示.劈裂破壞時的應力分布，如圖2所示.圖1，2中：α為混凝土破壞面與方鋼表面的夾角；Rr為徑向應力；F為摩擦力；P為壓應力；R為合力；μ為摩擦系數.當方鋼與混凝土之間產生相對滑移時，方鋼與混凝土表面會產生相對的滑移力，方鋼與混凝土之間由于產生了相對滑移，從而產生了新的作用面.方鋼和混凝土發生相對滑移直至混凝土界面破壞的過程中，理想的簡化模型將方鋼視作錐形體[29]，且混凝土破壞面覆蓋方鋼表面的肋間距，此時，混凝土破壞面與方鋼表面的夾角為α.在理想簡化模型中，方鋼與混凝土間的粘結力全部由混凝土與方鋼之間的摩擦力提供.

圖1 方鋼形狀簡化圖 圖2 劈裂破壞時的應力分布Fig.1 Simplified diagram of rebar shape Fig.2 Stress distribution at splitting failure

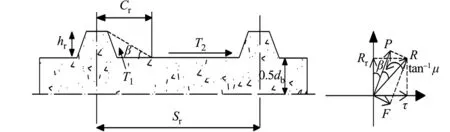
圖3 混凝土劈裂實際破壞面Fig.3 Actual failure surface of concrete splitting

國內外學者以該理想簡化模型為基礎進行研究發現，混凝土實際破壞時的界面角度并不是α，混凝土也無法完全覆蓋方鋼表面肋間距.在混凝土劈裂破壞時，破壞界面會形成一個楔形面[30]，如圖3所示.圖3中：hr為方鋼的肋高；Cr為楔形面底邊頂點到肋的距離；Sr為肋間距；db為方鋼邊長；T1為楔形面提供的拉拔力；T2為水平面的摩擦力.在方鋼混凝土劈裂破壞的瞬間，極限粘結應力主要由楔形面給予方鋼的拉拔力T1和楔形塊之外的方鋼表面與混凝土的摩擦力T2提供，除此之外，還有混凝土澆筑時產生的化學吸附力T3[31].

由于方鋼與圓鋼的截面形狀不同，導致方鋼與混凝土之間的握裹力與劈裂力的計算方法不同，使得方鋼與混凝土之間的粘結力與拉拔力計算方法不同[30].對于方鋼的徑向應力做如圖2所示的簡化處理.因此，根據混凝土破壞時的實際劈裂面，取一個肋間距Sr進行分析，可以推導得到破壞的楔形面上混凝土與方鋼的粘結應力τ1與徑向應力Rr的關系，即

(1)

式(1)中:β為假想的肋平面的傾斜角.

同時，方鋼總粘結應力τ與總拉拔力T存在關系為

(2)

式(2)中:lb為所取計算長度中方鋼的有效長度.

對照Wang[30]給出的公式，將圓鋼的理論模型加以改進，并考慮方鋼與混凝土的化學吸附力.方鋼在拉拔過程中，混凝土會給方鋼一個握裹力，假設方鋼會在劈裂時刻劈裂為兩半(圖2)，則劈裂時刻的楔形面部分的劈裂力Fsplit，1表示為

(3)

方鋼混凝土的總劈裂力Fsplit表示為

Fsplit=fctAsplit.

(4)

式(4)中:Asplit為混凝土的有效劈裂面積.

根據式(1)～(3)，可得

T1=4Fsplit，1tan(β+arctanμ)=4Crfctlsplittan(β+arctanμ).

(5)

式(5)中:lsplit為混凝土劈裂部分的長度.

水平面的摩擦力T2除去傾斜角β，可表示為

T2=4μFsplit，2=4μ(Sr-2Cr)fctlsplit.

(6)

式(6)中:Fsplit，2為方鋼水平面部分的劈裂力.

可以得到該肋間距中的楔形面與水平面的總拉拔力T為

T=T1+T2=4Fsplit，1tan(β+arctanμ)+4μFsplit，2.

(7)

將式(6)化簡，可得

(8)

根據拉拔力與粘結應力的關系，可以得出楔形面與水平面的總平均粘結應力τ1+τ2為

(9)

參考Martin[31]的建議，化學吸附力產生的粘結應力τ3取值為0.04fcu.總粘結應力可表示為

(10)

表2 各文獻的摩擦系數取值Tab.2 Values of friction coefficients in various literatures

3 方鋼-混凝土粘結應力理論模型

方鋼-混凝土的粘結應力與其摩擦系數有關.不同文獻的摩擦系數取值，如表2所示.綜合表2中各文獻摩擦系數的平均值，取方鋼與混凝土的摩擦系數μ為0.41進行后續分析.

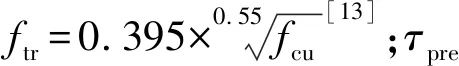
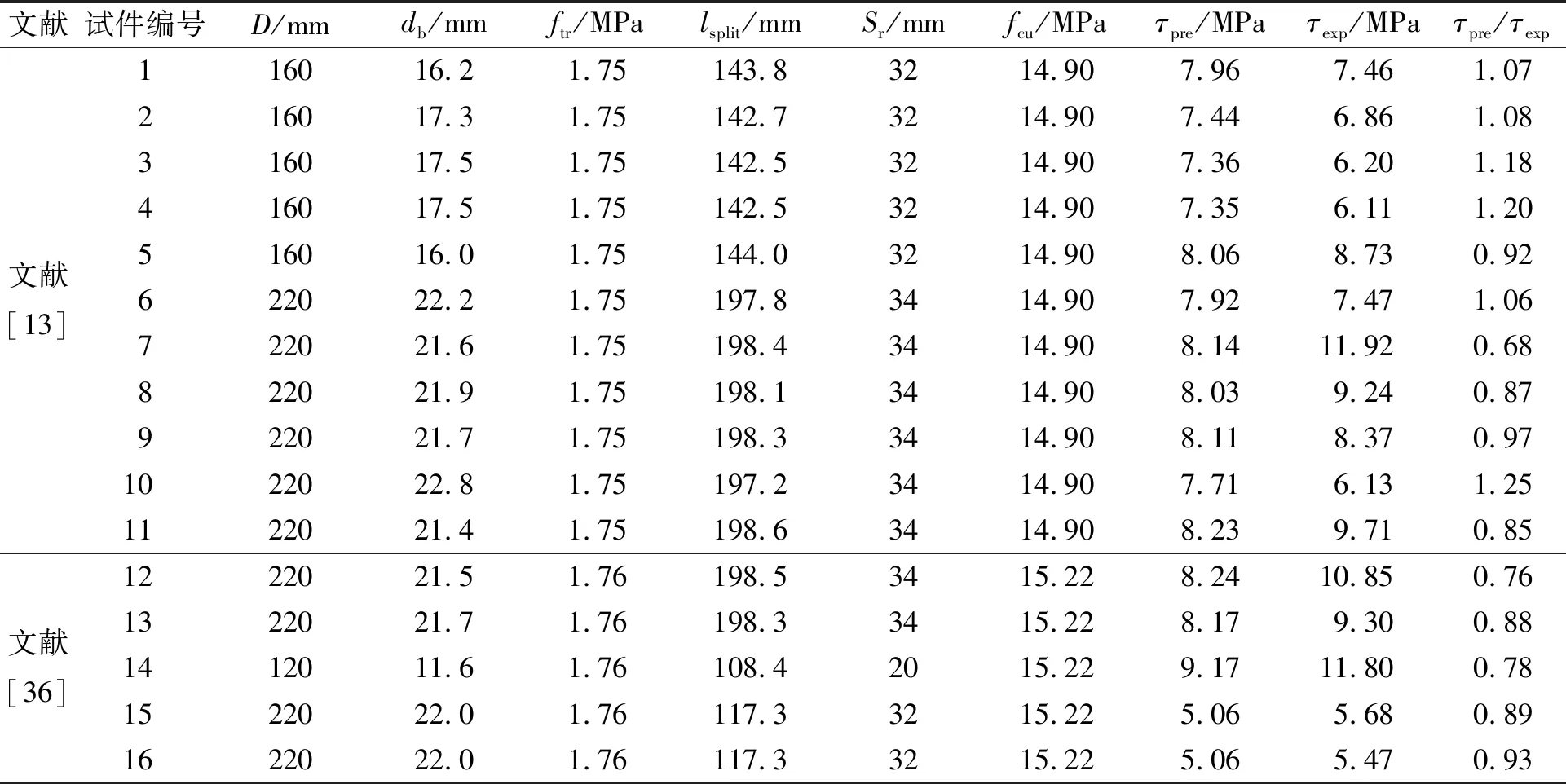
表3 文獻[13]和[36]試件極限粘結應力的試驗值和理論計算值對比Tab.3 Comparison between experimental value and theoretical calculation value of bond stress of specimens in literature [13] and [36]

根據表3中所得數據繪制散點圖，得到粘結應力理論計算值與試驗值的對比圖，如圖5所示.圖5中：k為斜率.由圖5可知：16個散點數據中有5個數據點明顯偏離了斜率(100±15)%的包絡線，積分誤差絕對值(IAE)為15.8%.此外，利用文中提出的理論公式得到的極限粘結應力的平均計算值與平均試驗值之比為1.08，證明該理論公式計算得出的方鋼-混凝土極限粘結應力具有較高的準確性.

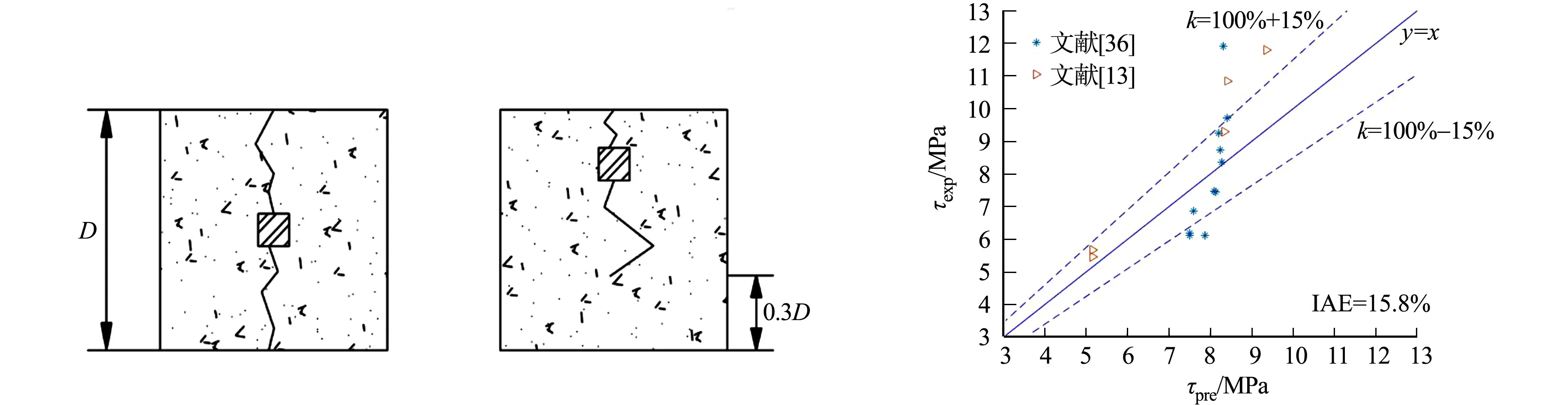
圖4 試件劈裂情況 圖5 理論計算值與試驗值對比Fig.4 Situation of specimen splitting Fig.5 Comparison between theoretical values and experimental values

4 參數分析

方鋼-混凝土的粘結應力主要與方鋼-混凝土的摩擦系數、方鋼的肋間距和肋高、混凝土的抗拉強度和抗壓強度及最終破壞的裂縫長度有關.從式(10)可以看出，混凝土相關強度參數越大，方鋼-混凝土的粘結應力也越大.但是，方鋼的肋間距Sr、肋高hr及方鋼邊長db和摩擦系數μ對粘結應力的影響并不能在公式中直觀地體現.因此，分析這4個參數對極限粘結應力的影響程度.

4.1 摩擦系數

選取表3中的5號試件進行參數分析(下同)，摩擦系數的取值范圍為0.2～0.6，其余參數不變.摩擦系數對極限粘結應力的影響，如圖6所示.

由圖6可知：摩擦系數對極限粘結應力的影響幾乎呈線性增長，摩擦系數越大，極限粘結應力就越大；當摩擦系數從0.2增長至0.6時，極限粘結應力從4.78 MPa增長至11.73 MPa，即摩擦系數增長到原來的3倍，極限粘結應力增長了145%.因此，摩擦系數對方鋼-混凝土粘結性能的影響較為顯著.

4.2 方鋼的肋間距

方鋼的肋間距的取值范圍為20～40 mm，其余參數不變，得到方鋼的肋間距對極限粘結應力的影響，如圖7所示.由圖7可知：方鋼的肋間距對極限粘結應力的影響呈反比例關系，肋間距越大，極限粘結應力越小；當方鋼的肋間距增長20 mm，即當方鋼表面肋間距增長到原來的2倍，極限粘結應力僅僅減小了11%.因此，方鋼的肋間距對方鋼-混凝土粘結性能的影響較小.

圖6 摩擦系數對極限粘結應力的影響 圖7 方鋼的肋間距對極限粘結應力的影響 Fig.6 Influence of friction coefficient on ultimate bond stress Fig.7 Influence of rib spacing of square rebar on ultimate bond stress

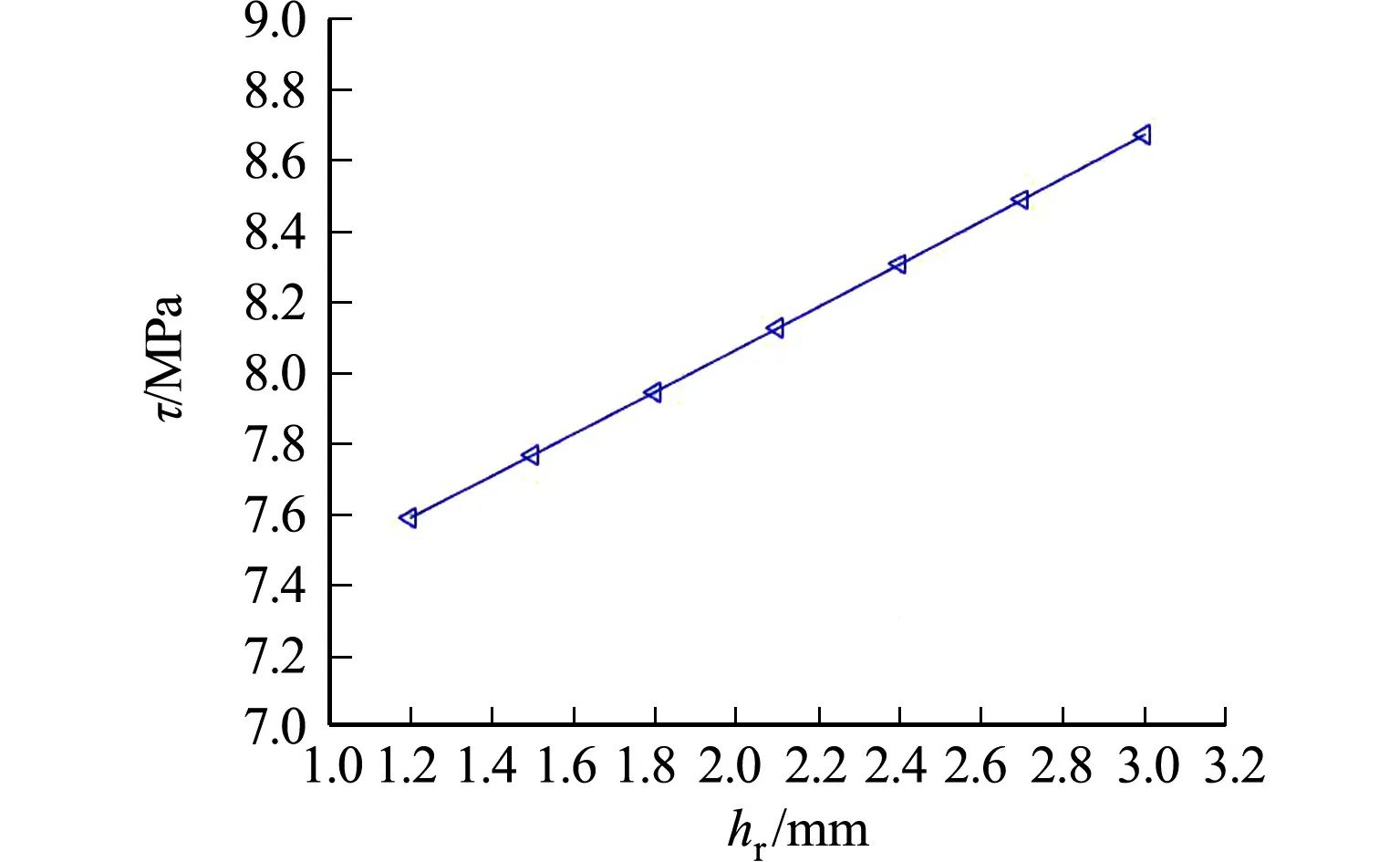
圖8 方鋼的肋高對極限粘結應力的影響Fig.8 Influence of rib height of square rebar on ultimate bond stress

4.3 方鋼的肋高

方鋼肋高取值范圍為1.2～3.0 mm，其余參數不變，方鋼的肋高對極限粘結應力的影響，如圖8所示.

由圖8可知：方鋼的肋高對極限粘結應力的影響與摩擦系數相仿，都是呈線性變化，且隨著方鋼肋高的增加，極限粘結應力也隨之增加，但是與摩擦系數稍有不同的是，方鋼肋高對極限粘結應力的影響并不是很大，由于近代方鋼的肋高大多為2 mm[14]，即使肋高在1～3 mm之間變動，劈裂時粘結應力的變化也不會超過1.2 MPa；且當肋高增大到原來的2.5倍，粘結應力僅增長了13%.

4.4 方鋼邊長

方鋼邊長的取值范圍為6～26 mm，其余參數不變，方鋼邊長對極限粘結應力的影響，如圖9所示.由圖9可知：方鋼邊長對劈裂時試件的極限粘結應力的影響呈反比例關系，方鋼邊長越大，極限粘結應力越小，當方鋼邊長擴大到24 mm時，試件劈裂時產生的極限粘結應力降低至原來的30.4%.

綜上所述，摩擦系數和方鋼的肋高與方鋼-混凝土極限粘結應力均呈線性關系，且均為正比例關系，其中，摩擦系數對粘結滑移性能的影響較大，方鋼的肋高對粘結滑移性能的影響較小.方鋼的肋間距及方鋼邊長與方鋼-混凝土極限粘結應力呈反比例關系，肋間距越大，極限粘結應力越小，但影響程度偏小.而方鋼邊長對方鋼-混凝土劈裂時的極限粘結應力的影響相對肋間距來說更大，且方鋼邊長db<16 mm時對極限粘結應力的影響較方鋼邊長db>16 mm時的影響更大.

4.5 近代方鋼-混凝土粘結性能與現行規范的比較

近代歷史文獻采用安全值的方法規定方鋼-混凝土的極限粘結應力為0.5～0.8 MPa.我國現行國標GB 50010-2010《混凝土結構設計規范》[27]建議用四段式折線(粘結滑移曲線，粘結應力為縱坐標，相對滑移值為橫坐標)表示方鋼-混凝土的粘結性能，采用3個特征點確定四段折線，分別為(0.025Scr，2.5ftr)，(0.040Su，3.0ftr)，(0.550Sr，ftr)，其中，Scr為劈裂段的最大相對滑移；Su為失效階段的最大相對滑移；Sr為殘余段的最小相對滑移.可見現行的混凝土規范對極限粘結應力的規定僅與混凝土的強度有關.取近代混凝土立方體強度抗壓標準值15 MPa，則現行規范規定的方鋼-混凝土極限粘結應力為2.73 MPa.

根據上文的參數分析，取方鋼的肋高為2.0 mm，摩擦系數為0.41，混凝土試塊邊長為160 mm且假設破壞時混凝土試塊截面均劈裂，方鋼肋間距的取值范圍為20～44 mm，方鋼邊長取12～26 mm，計算得到方鋼-混凝土的極限粘結應力理論值為4.69～11.83 MPa.對比表1中的數據可知，近代文獻和現行規范對極限粘結應力設計值的規定都相對保守，尤其對于近代文獻規定值來說，極限粘結應力規定的最大值約為理論計算最小值的0.17倍.

5 結論

對近代歷史文獻中方鋼-混凝土粘結性能的相關規定進行整理分析，基于方鋼的構造特征，提出方鋼-混凝土極限粘結應力的理論計算模型，得出以下3點結論.

1) 近代中國歷史文獻中規定的極限粘結應力非常保守，約為現行混凝土規范中規定的同等級混凝土與帶肋方鋼的極限粘結應力的0.19～0.29倍.

2) 依據方鋼-混凝土粘結滑移性能的楔形截面破壞理論，文中提出的方鋼-混凝土極限粘結應力的計算方法的理論計算值與試驗值的平均比值為1.08，IAE為15.8%，證明理論公式的準確度較高.

3) 影響近代方鋼-混凝土極限粘結應力的因素主要為混凝土與方鋼的摩擦系數，方鋼的肋間距、肋高和邊長；摩擦系數和方鋼的肋高對于極限粘結應力的影響為正相關，其中，摩擦系數的影響較大；方鋼的肋間距和方鋼邊長對極限粘結應力的影響為負相關，其中，方鋼邊長的影響較大.