數(shù)值求解納米尺度熱傳導(dǎo)分?jǐn)?shù)階拋物兩步模型

沈淑君

(1.華僑大學(xué) 數(shù)學(xué)科學(xué)學(xué)院，福建 泉州 362021；2.華僑大學(xué) 計(jì)算科學(xué)福建省高校重點(diǎn)實(shí)驗(yàn)室，福建 泉州 362021)

納米傳熱現(xiàn)象的模擬已經(jīng)引起人們的廣泛關(guān)注，特別是超短脈沖激光加熱引起的納米尺度熱傳導(dǎo).由于效率高、功率密度高、附帶材料損壞小、加熱高精度控制等優(yōu)點(diǎn)，超短脈沖激光加熱技術(shù)已廣泛應(yīng)用于生物、化學(xué)、醫(yī)學(xué)、物理和其他的熱加工領(lǐng)域，如薄金屬薄膜的結(jié)構(gòu)監(jiān)測(cè)，激光微加工，激光微薄膜的制圖、結(jié)構(gòu)裁剪和薄膜沉積中的激光加工等[1].分?jǐn)?shù)階微分算子具有非局部性，非常適用于描述現(xiàn)實(shí)世界中具有記憶及遺傳性質(zhì)的材料，已成為描述各類復(fù)雜力學(xué)和物理行為的重要工具之一[2].分?jǐn)?shù)階微積分已成功地應(yīng)用于多種熱傳導(dǎo)模型的模擬和研究[3-5]，分?jǐn)?shù)階模型已被證實(shí)是一個(gè)很好的納米級(jí)傳熱的候選者[6].繼續(xù)研究文獻(xiàn)[1]中的分?jǐn)?shù)階拋物型兩步超短脈沖激光加熱引起的納米級(jí)熱傳導(dǎo)模型，即

(1)

(2)

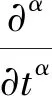
(3)

1892年，Hadamard提出了Hadamard分?jǐn)?shù)階導(dǎo)數(shù)[10]，這種分?jǐn)?shù)階導(dǎo)數(shù)與Riemann-Liouville和Caputo分?jǐn)?shù)階導(dǎo)數(shù)的區(qū)別在于積分核含有任意指數(shù)的對(duì)數(shù)函數(shù).研究者發(fā)現(xiàn)，Hadamard分?jǐn)?shù)階微積分在描述材料疲勞裂紋擴(kuò)展方面具有潛在的應(yīng)用價(jià)值[11-14].但是，Riemann-Liouville導(dǎo)數(shù)和Hadamard導(dǎo)數(shù)的其中一個(gè)缺點(diǎn)就是對(duì)常數(shù)的導(dǎo)數(shù)一般不等于零.2012年，Jarad等[7]修改了Hadamard分?jǐn)?shù)階導(dǎo)數(shù)，使其對(duì)一個(gè)常數(shù)的導(dǎo)數(shù)為零，并且使其在物理上具有類似于Caputo分?jǐn)?shù)階導(dǎo)數(shù)那樣的可解釋的初始條件，由此產(chǎn)生了Caputo-Hadamard分?jǐn)?shù)階導(dǎo)數(shù).比起Hadamard分?jǐn)?shù)階導(dǎo)數(shù)，Caputo-Hadamard分?jǐn)?shù)階導(dǎo)數(shù)更適合應(yīng)用在工程和科學(xué)中[7，10，14].

與文獻(xiàn)[1]做法一樣，引入無量綱參數(shù)，便得到無量綱的分?jǐn)?shù)階拋物型兩步熱傳導(dǎo)模型為

(4)

(5)

式(4)中：Kn表示Knudsen數(shù).

此外，需要指出的是，在考慮納米級(jí)傳熱時(shí)[15]，非跳溫邊界條件忽略了邊界聲子散射的影響，導(dǎo)致在邊界附近的結(jié)果令人不滿意.通過觀察發(fā)現(xiàn)，碳納米管的熱流是阻塞的，溫度在管的兩端可以看到跳躍[16-17].為了捕捉納米幾何結(jié)構(gòu)內(nèi)部的邊界聲子散射效應(yīng)，提出溫度跳躍(Robin′s)邊界條件[1]，即

(6)

為使記號(hào)簡(jiǎn)單，采用u(x，t)和v(x，t)分別代替模型中的Te(x，t)和Tl(x，t).

1 模型方程

考慮無量綱分?jǐn)?shù)階兩步模型，即

(7)

(8)

帶有Robin邊界和初值條件為

(9)

u(x，a)=T1(x)，v(x，a)=T2(x)，x∈[0，1].

(10)

(11)

同理，用類似的過程可以得到v(x，t)的第2個(gè)邊界條件為

(12)

2 緊有限差分格式

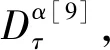
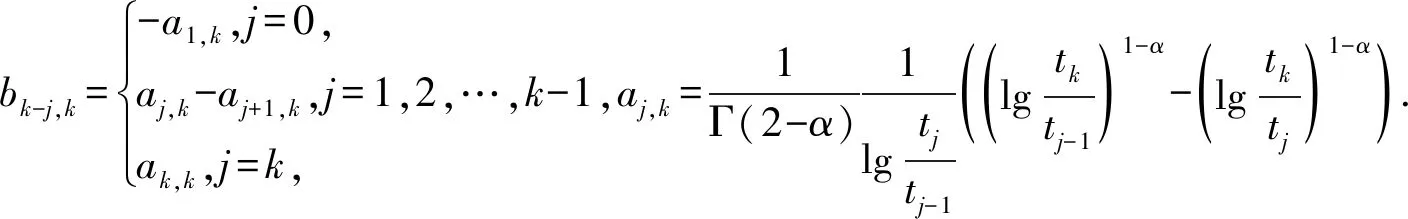
引理1[1]如果f(x)∈C6[x0，xM] ，則有

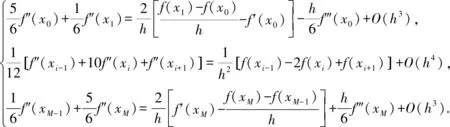
引理2[9]設(shè)0<α<1，g(t)∈C2[a，tk]，則有

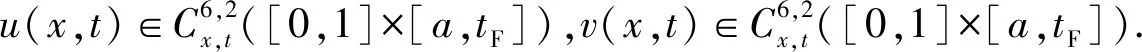
(13)

(14)

(15)

(16)

把邊界條件(9)和方程(16)一起代入方程(14)，可得

(17)

(18)

于是，方程(17)變?yōu)?/p>

(19)

同理，用類似上面的過程可以推導(dǎo)出當(dāng)i=M時(shí)方程(7)的緊格式為

(20)

當(dāng)1≤i≤M-1時(shí)，利用引理1，2可得

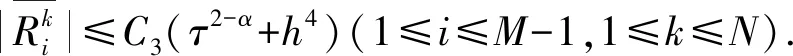
(22)

(23)

(24)

(25)

(26)

(27)

式(23)～(26)中:1≤k≤N.

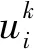
備注2用類似文獻(xiàn)[1]中的能量分析的方法可以證明差分格式(23)～(27)是穩(wěn)定的，并且收斂階為O(τ2-α+h4).

3 數(shù)值算例

考慮帶Robin邊界的Caputo-Hadamard分?jǐn)?shù)階拋物型兩步模型，即

(28)

(29)

(30)

u(x，1)=0，v(x，1)=0，x∈[0，1].

(31)

式(28)，(29)中:0<α<1.

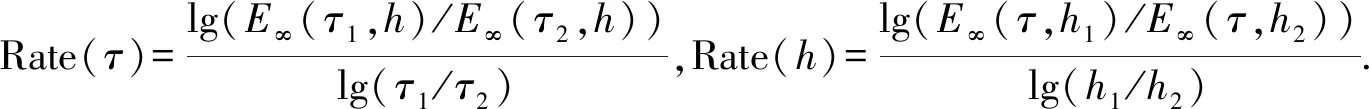
當(dāng)時(shí)間tF=2，空間步長(zhǎng)h=1/50時(shí)，隨著時(shí)間步長(zhǎng)τ的減少，取不同時(shí)間分?jǐn)?shù)階α?xí)r，例1數(shù)值解的最大誤差和時(shí)間上的收斂階的情況，如表1～4所示.表1～4中：EU，max，EV，max分別為U，V的最大誤差；RateU，RateV分別為U，V的收斂階.

表1 α=0.2 時(shí)的最大誤差和時(shí)間上的收斂階(例1)Tab.1 Maximum errors and convergence rates in time for α=0.2 (example 1)

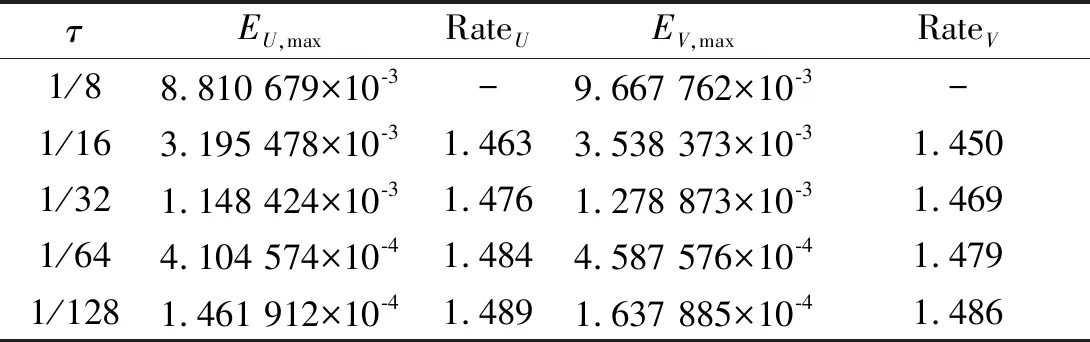
表2 α=0.5 時(shí)的最大誤差和時(shí)間上的收斂階(例1)Tab.2 Maximum errors and convergence rates in time for α=0.5 (example 1)

表3 α=0.8 時(shí)的最大誤差和時(shí)間上的收斂階(例1)Tab.3 Maximum errors and convergence rates in time for α=0.8 (example 1)

表4 α=0.999 時(shí)的最大誤差和時(shí)間上的收斂階(例1)Tab.4 Maximum errors and convergence rates in time for α=0.999 (example 1)

由表1～4可知：時(shí)間上的收斂階大概是2-α.這與引理2的結(jié)論吻合.

當(dāng)時(shí)間tF=2，時(shí)間分?jǐn)?shù)階α=0.5，τ=1/20 000時(shí)，隨著空間步長(zhǎng)的減少，例1數(shù)值解的最大誤差和空間上的收斂階，如表5所示.由表5可知：空間上的收斂階大概是4階.

表5 α=0.5時(shí)的最大誤差和空間上的收斂階(例1)Tab.5 Maximum errors and convergence rates in space for α=0.5 (example 1)

源項(xiàng)

參數(shù)取為B=G=c0=Kn=1.可以算出精確解為

當(dāng)時(shí)間tF=2，h=1/50時(shí)，隨著時(shí)間步長(zhǎng)的減少，取不同的時(shí)間分?jǐn)?shù)階α?xí)r，例2數(shù)值解的最大誤差和時(shí)間上的收斂階，如表6～9所示.

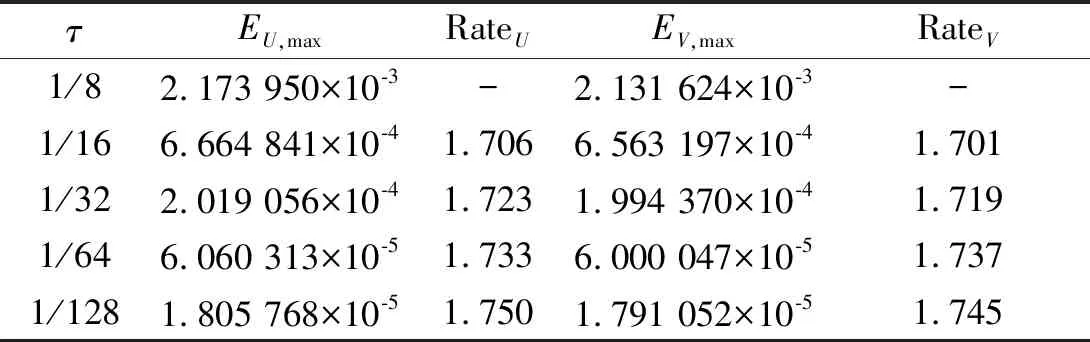
表6 α=0.2 時(shí)的最大誤差和時(shí)間上的收斂階(例2)Tab.6 Maximum errors and convergence rates in time for α=0.2 (example 2)

表7 α=0.5 時(shí)的最大誤差和時(shí)間上的收斂階(例2)Tab.7 Maximum errors and convergence rates in time for α=0.5 (example 2)

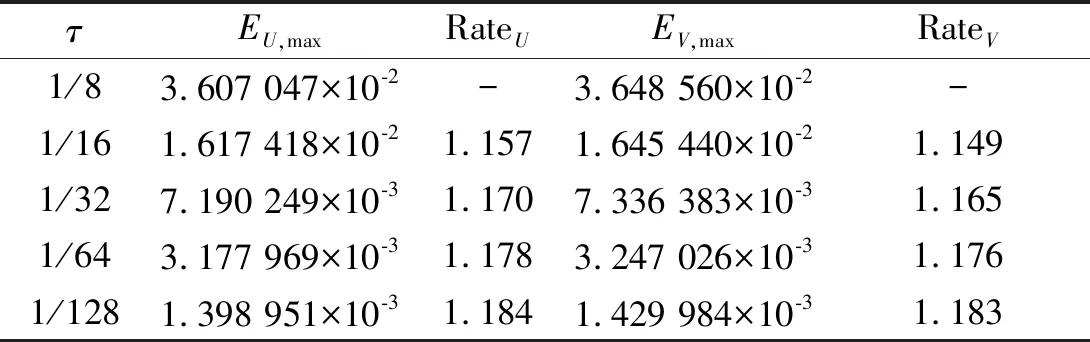
表8 α=0.8 時(shí)的最大誤差和時(shí)間上的收斂階(例2)Tab.8 Maximum errors and convergence rates in time for α=0.8 (example 2)

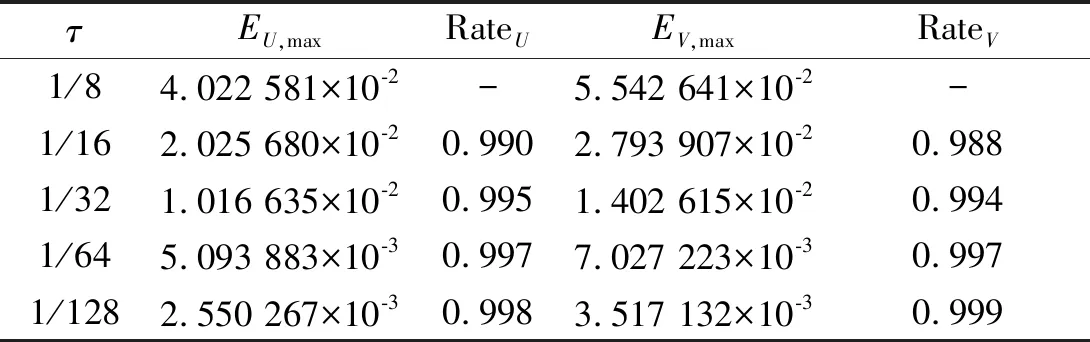
表9 α=0.999 時(shí)的最大誤差和時(shí)間上的收斂階(例2)Tab.9 Maximum errors and convergence rates in time for α=0.999 (example 2)

由表6～9可知：時(shí)間上的收斂階大概也是2-α，這與引理2的結(jié)論吻合.

當(dāng)時(shí)間tF=2，α=0.2，τ=1/20 000時(shí)，隨著空間步長(zhǎng)的減少，例2數(shù)值解的最大誤差和空間上的收斂階，如表10所示.由表10可知：空間上的收斂階也大概是4階.

表10 α=0.2 時(shí)的最大誤差和空間上的收斂階(例2)Tab.10 Maximum errors and convergence rates in space for α=0.2 (example 2)

4 結(jié)束語

對(duì)無量綱的分?jǐn)?shù)階拋物型兩步熱傳導(dǎo)模型提出了高階有效的數(shù)值算法.方程中采用的是Caputo-Hadamard分?jǐn)?shù)階導(dǎo)數(shù)，并且考慮的是Robin邊界條件，目前國(guó)內(nèi)外文獻(xiàn)還鮮有研究.利用空間四階緊格式和Caputo-Hadamard時(shí)間分?jǐn)?shù)階導(dǎo)數(shù)的L1逼近格式建立了數(shù)值格式.文中的兩個(gè)數(shù)值例子驗(yàn)證了提出的數(shù)值算法的有效性.通過改變Knudsen數(shù)和分?jǐn)?shù)階導(dǎo)數(shù)的數(shù)值以及邊界條件中的參數(shù)，模擬可以作為分析超短脈沖激光作用下多孔介質(zhì)(如多孔金屬薄膜)納米尺度熱傳導(dǎo)的工具.后續(xù)可進(jìn)一步深入探索算法的理論研究.