真空-堆載預壓聯合加固道路軟基沉降規律研究

黃艷軍，張艷林，劉夕奇，王 聰，王東星

（1.中國水利水電第七工程局有限公司，四川成都 610213；2.武漢大學 土木建筑工程學院，湖北武漢 430072)

引言

我國海岸線大部分屬淤泥質海岸，土體為淤泥、淤泥質粘土、淤泥質亞粘土，具有初始含水率高、抗剪強度低、孔隙率高、壓縮性強、透水性欠佳等復雜特征[1]。若將建筑物修建于此類軟弱土地基，固結過程及剪切效應將誘使地基產生延續時間很長的顯著沉降甚至不均勻沉降，地基土體自身低強度誘發地基承載與穩定性難以滿足實際工程要求。為能夠確保施工運營期軟弱地基穩定性與承載力、有效控制過大差異沉降，通常不得不預先對軟弱土地基開展加固增強處治[2-3]。

通過抽真空與堆載聯合作用加固地基，真空預壓旨在降低孔隙水壓、增大有效應力，堆載預壓旨在增大總應力以提高孔隙水壓、轉化為有效應力，二者共同作用確保地基不會因填土速率過快而失穩。真空-堆載預壓法，已普遍推廣應用于多類型、不同領域實際工程，加固效果和經濟效益顯著。許多學者已對該技術進行系統深入探索，取得了豐碩成果。陳環和鮑秀清[4]用一維負壓固結儀開展正負壓對比試驗，分析所得數據發現正壓、負壓下固結過程基本相同；Leong 等[5]探究相同正負壓力值下試樣剪切強度演變過程，分析發現堆載預壓加固地基效果要優于真空預壓；張誠厚等[6]選用模型槽試驗探究排水板間距、真空面位置影響地基加固效果，揭示真空作用面移向低部后地基加固效果更好且排水板間距對其影響不容忽略；沈珠江和陸舜 英[7]選取Biot 固結有限元計算某真空預壓法加固地基工程，發現本構模型選取對模擬數據影響很大且認為南水模型計算結果比較符合實際；劉漢龍等[8]、王旭升和陳崇希[9]等學者開展有限元和邊界元在真空預壓計算方面應用，拓展了真空聯合堆載預壓法理論深度及工程示范；吳躍東等[10]依托京珠高速廣東段某軟基真空-堆載加固工程，綜合殷宗澤雙屈服面等本構模型，數據表明考慮土體流變計算結果優于僅考慮彈塑性變形計算結果。

以真空-堆載預壓加固廣州某地基工程為依托，綜合考慮荷載形式、初始條件和邊界條件建立有限元數值計算模型，明確真空-堆載預壓下軟土地基沉降演變過程和孔壓傳遞規律并與實測數據對比，最后基于所得結果預測堆載中心點處工后沉降。研究成果可為廣州市洪灣港等工程建設安全及工期優化提供理論支撐。

1 工程概況

1.1 工程背景

工程位于廣州市南沙區某填筑項目道路軟基加固工程，沉積軟土區域占施工占地總面積50 %～60 %，片區擬建市政道路約80 %軟基需利用真空聯合堆載預壓法加固。典型軟土區域某試驗段，分段加固區長214.8 m，兩端寬40 m。

1.2 地質條件

片區處于廣州某典型深厚軟土地帶，地層自上而下依次：人工填土層、第四系海陸交互相沉積層、殘積層、下伏基巖為燕山三期侵入花崗巖。該路段地基土層和土體計算參數，見表1。

表1 加固區土體地質參數

1.3 排水板選擇與布置方式

塑料排水板因性能好、質量可靠、施工方便、工效高等優點，獲得了廣泛的應用。塑料排水板采用SPB100·C 型原生料板（厚度4.5 mm、寬度 100 mm），排水板按正三角模式打設、打設間距 1 m，平均深度21 m，濾管（Φ50 mm）及主管 （Φ75 mm、壁厚≥2.3 mm）選取PVC 材質，采用高強度柔性塑料波紋濾管。

2 軟基固結沉降數值模擬

2.1 有限元計算參數

有限元平面計算模型中，將排水板等效為砂井，使等效后圓柱狀砂井與塑料排水板具有相同排水能力，此時砂井直徑設定為排水板等效直徑。有必要將軸對稱砂井地基問題轉換為平面應變問題處理，轉化原則是保證轉化前后地基平均固結度固定。把沿路基縱向間隔排布砂井視為沿縱向連續排布砂墻，即把砂井地基（三維固結問題）轉變為成排砂墻地基（平面應變問題）。依據現有計算原則與等效方法，塑排板不同計算參數及其取值，見表2。

表2 塑排板參數及其取值

2.2 有限元計算模型

利用軸對稱性，取整個軟土地基的一半建立模型。計算模型幾何參數，基本與原型施工時相同。路基頂面寬度40 m，由于計算斷面對稱，計算時取路基寬度20 m。考慮真空-堆載聯合預壓豎向影響深度和水平影響范圍，取基本不受影響的粉砂層厚度50 m，相當于被影響深度范圍2 倍。塑料排水板總長23 m，厚度4.5 mm，間距1.1 m。

采用孔隙流體/應力耦合單元CPE4P 進行有限元網格劃分，模型網格劃分如圖1 所示。將加固區土體網格進行加密，使加固區計算結果更精確，遠離加固區土體所受影響越小，網格逐漸稀疏。計算模型設定邊界條件：左右邊界設置為不透水邊界（僅豎向變形），底面邊界設置為不透水界面（豎向/水平變形為零），頂面邊界設置為自由位移邊界，且地表邊界設置為零孔隙水壓。

圖1 有限元網格劃分

3 模型加載

3.1 計算荷載步確定與初始地應力平衡

為準確計算，分四個載荷步施加真空-堆載加載時程曲線，如圖2 所示。第一載荷步是施加初始地應力；第二荷載步是施加瞬時真空負壓，該荷載步只有一個子步；第三荷載步是繼續施加真空負壓；第四荷載步是同時施加路基堆載和真空壓力（加載持時230 d）。第三、第四荷載步，設置為自動時步。

圖2 真空-堆載時程曲線

計算過程中須簡化荷載，真空聯合堆載預壓時荷載形式主要為土體自重、加固區土體表面堆載壓力和排水體中真空負壓。跟據工程實際情況，堆載分三次實施進行，加固區真空預壓：表面點孔壓從0 線性漸近衰減至-80 kPa 后恒定；加固區堆載預壓：按填土堆載過程實施、不必等效轉換。地表真空壓力達到-80 kPa，加固深度底部壓力-15 kPa，通過在Abaqus 設置場函數得以實現。

3.2 模擬與實測沉降結果對比

數值模型的堆載中心點對應軟基地表沉降計算值隨時間變化過程，見圖3（包含現場監測沉降量數據）。分析可知，簡化計算模擬值同實測值吻合程度較高，但與實測值存在一定差異。真空預壓區域軟基沉降整體比較均勻，中心點地表沉降實測值210 cm，此時對應模擬值217 cm，二者誤差約3.4 %。

圖3 加固區中心點地表沉降模擬值與實測值

選取計算模型堆載中心點下不同深度處地基沉降模擬值隨時間變化曲線，見圖4（包含現場實測沉降數據）。分析發現，真空預壓作用之初，軟基沉降數值計算值與實測值之間存在差異，最大誤差不高于20 %。究其原因，工程實際中負孔隙水壓力傳遞是隨時間和深度變化漸進過程，受傳遞過程阻力效應、施工場所復雜程度、地基土不均勻性等因素制約，且未全面考慮井阻、涂抹等作用，模擬所得沉降曲線收斂較快。上述因素可能是導致模擬計算值和實測值二者存在誤差的原因，但模擬計算值和實測值總體發展趨勢一致。

圖4 分層沉降模擬值與監測值曲線

分析發現，由于所構建數值模型、參數取值等方面不可避免與現場真實情況仍有差異，并不能夠理想再現地基土實際應力-應變特性，但數值計算數據整體還是較為合理，無論是位移變化趨勢還是位移量基本上均與實測值契合。隨著時間延續，地基土側向水平和豎向沉降量均加大，真空-堆載協同作用加固效果明顯、路基變形顯著。堆載固結過程中，軟基沉降模擬結果與實測值變化規律一致。等值線圖表明地基加固區發生漏斗狀沉降變形，且中心處沉降量最大、向外側邊緣沉降量緩慢減小。值得注意的是，真空預壓地基25 m 深度范圍內沉降量偏大，意味著加固效果主要集中在25 m 深度范圍，即約為排水板打設深度。

真空-堆載預壓作用增強路基影響范圍較廣，邊緣外側6 m 之內路基土仍然會發生豎向沉降。究其原因，加固區地基土受真空與堆載聯合作用的影響程度遠小于中心點處賦存土體，地基土出現朝向加固區方向的水平位移；堆載作用促使加固區地基土朝外側壓擠，導致加固區臨近土體沉降值比中心點處小，這跟現場實測數據較為契合。

3.3 模擬與實測孔壓結果對比

圖5 為地基膜下真空度與模型加載時程曲線。圖6 為堆載中心點不同深度處孔隙水壓力監測值與數值模擬對比結果。

圖5 膜下真空度隨時間變化

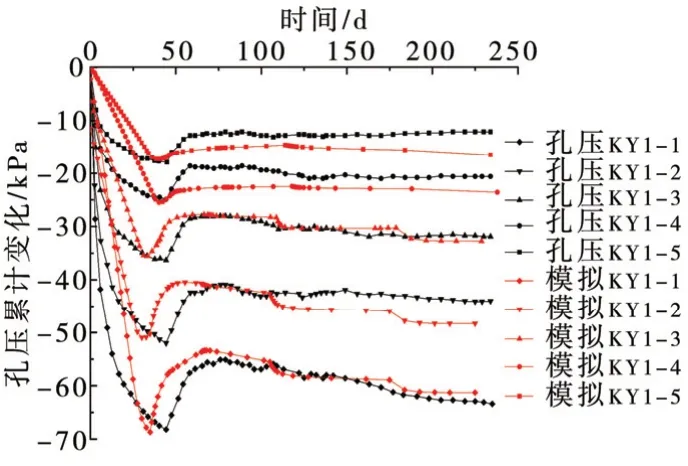
圖6 中心不同深度處孔壓與模擬結果對比

分析可知，盡管孔隙水壓力數值計算值與現場實測值不可避免存在差異，不過整體演變趨勢較為相符，即孔隙水壓力值隨抽真空啟動而快速降低，隨抽真空時間增加，孔隙水壓降幅漸趨縮小。堆載預壓固結過程中，堆載作用下地基土內部孔壓迅速增大，而孔壓及時有效消散后土體固結沉降過程方可逐漸完成。分析超靜孔壓計算與實測數據二者時程曲線，可發現：1）堆載加固地基土內部孔壓增幅和孔壓消散速率隨深度增加而減弱；2）現場監測和數值計算數據二者演變規律相符，堆載導致孔壓明顯增加，經由塑排板排水固結、孔壓漸趨消散；3）預壓作用區域之外密封帷幕的存在導致真空負壓向外傳遞受阻，表現為真空負壓傳遞范圍集中在預壓區域內；4）孔壓現場實測與計算數據之間存在些許差異，計算值對應峰值相較實測數據更為顯著，并且實際孔壓消散速率明顯弱于計算速率，這源于所構建數值模型的計算簡化和并未引入井阻效應，進而引起一定程度波動。

3.4 水平位移計算結果

水平位移計算曲線，見圖7，其中位移以向加固區方向移動為正。從圖9 可知，地基土水平位移的計算與實測數據整體上相符合。真空預壓引起地基土發生朝向加固區變形；堆載作用（較真空荷載小）施加導致地基土水平位移規律演變，但其方向仍然朝向加固區，盡管土體位移相較真空預壓時已有所減小。從圖10 可知，地基土側向變形主要發生在加固區范圍邊緣地表，區內外土體均朝向內側移動，向內位移量與距加固區邊緣距離成反比，該現象與現場數據規律較為吻合。同時，密封墻外側地基土變形量明顯比其內側更小，即發現密封墻兼具密封和阻礙非加固區水平位移效能。上述分析表明，真空預壓作用能夠引起一定程度的朝向內側位移，而且其影響作用范圍比較廣、即需考慮施工過程對周邊環境干擾。

圖7 水平位移監測與數值模擬結果對比

4 工后沉降預測

選取Asaoka 法進行真空-堆載聯合預壓加固地基工后沉降預測，理論基礎是一維固結方程。采用Asaoka 法（淺崗法）分析固結度，Δt 過小，會造成擬合點跳躍性較大，擬合所得直線相關系數較小；Δt 過大，擬合參數偏小，會產生一定偏差。因此，建議Δt 取值區間為10～100 d，選取Asaoka 法通過線性擬合預測地基沉降。線性擬合結果的好壞，通過相關系數反映，相關系數越大，則擬合結果可信度越高，擬合參數誤差就越小。

如圖8 和圖9 所示，選取Δt=10 d，根據Asaoka法進行固結系數反演計算，工程現場及數值模擬得到相關系數分別為0.981 和0.93，說明預測結果可靠性較高。聯港二路GK0+336.000～+550.797 段預測結果，見表3。截至2021 年6 月11 日滿載驗收后抽真空125 d，符合設計要求的預壓期≥120 d。分析表3 可知，Asaoka 法推算得到的實測值及模擬值最大工后沉降均≤50 cm，符合設計要求（次干路15年、支路10 年，一般路段≤50 cm）。經綜合評定，該區域軟基處理加固達到設計卸載要求，建議真空卸載。

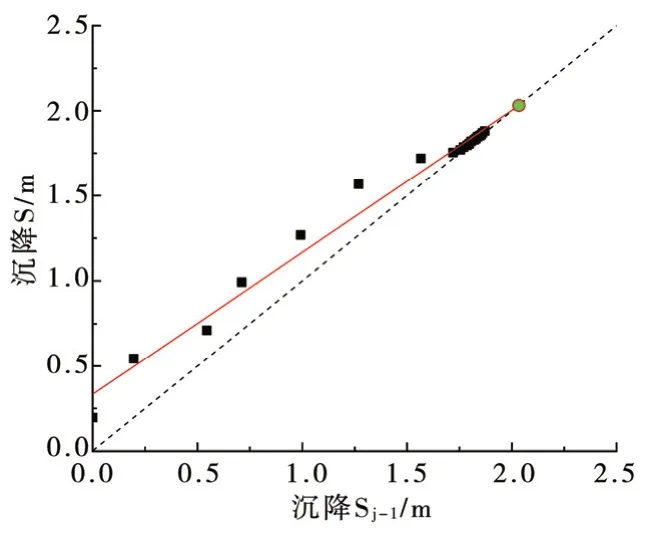
圖8 堆載中心點沉降預測

圖9 數值模擬沉降預測

表3 Asaoka 法固結度推算

5 結語

依固結度等效原則將砂井地基轉化為砂墻地基，提出一種真空-堆載聯合預壓有限元計算簡化方法，建立廣州南沙區某典型軟土區域真空-堆載聯合加固道路軟基有限元模型。結論如下：

1）通過數值計算值和現場實測數據分析比對，基于Abaqus 軟件的有限元計算模擬真空-堆載預壓加固軟基計算過程與實測數據較為吻合，即有限元簡化計算方法能夠有效模擬真空-堆載預壓加固軟基過程。

2）真空預壓加固區地基土主要產生收縮變形，并引起加固區域之外土體朝向加固區域方向移動；堆載預壓效應導致加固區地基土向外側壓擠，而近地表地基土仍然主要發生收縮變形，這與真空-堆載聯合預壓工作機理相一致。

3）根據實測沉降曲線，采用Asaoka 法推算預測最大工后沉降均≤50 cm，符合設計要求。經綜合評定，該區域道路軟基處理加固達到設計卸載要求，建議真空卸載。