挖掘教材資源 夯實單元復(fù)習*

范建兵 (江蘇省蘇州高新區(qū)景山實驗初級中學校 215163)

董林偉先生曾說過，數(shù)學學習的規(guī)律一般為先進行知識的新授課學習，再逐步深入，最后通過反思進行復(fù)習鞏固提升，從而對知識形成整體性的認識.新授課主要解決三個問題：為什么學、學什么、怎么學，而復(fù)習課則相應(yīng)解決知識間有怎樣的實質(zhì)聯(lián)系、知識如何運用、知識運用的智慧在哪里三個問題[1].數(shù)學教材是學生數(shù)學學習最普及、最有效的工具，是最能體現(xiàn)數(shù)學課程標準的教學資源.在單元復(fù)習教學中，應(yīng)立足于課程標準的精準要求，在宏觀上理解單元教學內(nèi)容在整個教材中的地位和作用，從微觀上把握單元教學內(nèi)容所蘊含的四基，深入研究教材，統(tǒng)整核心內(nèi)容，挖掘教材內(nèi)涵，凸顯教材的基礎(chǔ)功能和教學價值，達成知識更清楚、結(jié)構(gòu)更清晰、思路更明確、學習更有效的復(fù)習目標，提升學生學習自信與理性精神.現(xiàn)以人教版七年級下冊第五章《平面直角坐標系》為例，結(jié)合教材所提供的教學資源，談?wù)剬卧獜?fù)習的思考.

1 以問理知：梳理核心知識，增強問題意識

問題是數(shù)學的心臟，數(shù)學課堂教學本質(zhì)上是對問題的教學.好的問題具有兩個特征：一是基于學生認知，符合學生的最近發(fā)展區(qū)，能夠驅(qū)動學生主動思考、積極探究、互動交流；二是符合教師的教學風格，有利于教師引導(dǎo)學生實現(xiàn)高質(zhì)量和高立意；能把培養(yǎng)學生的問題意識、提高學生提出問題和解決問題的能力貫穿于整個問題之中[2].高效的單元復(fù)習應(yīng)該以問題為載體，將整個單元涉及的概念、性質(zhì)、應(yīng)用等數(shù)學知識統(tǒng)整起來，將復(fù)雜的、抽象的數(shù)學知識以問題的形式生動靈活地呈現(xiàn)在學生面前.人教版教材第83頁設(shè)置了如下問題供復(fù)習選用.

1.在日常生活中，我們可以用有序數(shù)對來描述物體的位置.以教室中座位位置為例，說明有序數(shù)對(x，y)和(y，x)是否相同以及為什么.

2.平面直角坐標系由兩條互相垂直且有公共原點的數(shù)軸組成.請你舉例說明如何建立平面直角坐標系，在直角坐標平面內(nèi)描出點P(2，4)和原點的位置，并指出點P和原點的橫坐標和縱坐標.

平面直角坐標系的兩條坐標軸將平面分成I，II，III，IV四個部分，這四個部分依次稱為第一象限、第二象限、第三象限和第四象限.請你在直角坐標平面內(nèi)描出點A(2，1)，B(-2，1)，C(-2，-1)，D(2，-1)的位置，并說明它們所在的象限.

3.平面直角坐標系具有廣泛的應(yīng)用,請你舉例說明它的應(yīng)用.

復(fù)習體系中的問題，一般都應(yīng)具有代表性和指向性，能夠在掌握知識技能、提升思維能力、激發(fā)數(shù)學興趣、開闊數(shù)學視野及培養(yǎng)創(chuàng)造精神等方面發(fā)揮重要的作用.以上幾個問題不僅有常規(guī)性問題(知識指向)，也有開放性問題(應(yīng)用指向)，能夠考查學生的判斷力、理解力和創(chuàng)造力.問題1意在讓學生理解坐標的有序性，從而認識到學習平面直角坐標系的必要性；問題2意在讓學生認識平面直角坐標系中的相關(guān)概念，感悟數(shù)與形的相互轉(zhuǎn)化；問題3開放而多元，指向數(shù)學的應(yīng)用性和價值性，引導(dǎo)學生用數(shù)學的眼光觀察世界，理解數(shù)學源于生活又服務(wù)于生活.復(fù)習時通過對章節(jié)核心問題的提出與思考，引導(dǎo)學生全面梳理知識并加深理解記憶.這種問題的設(shè)計既要有知識性和藝術(shù)性，更要有指向性和整體性.除了上述問題，復(fù)習中還可以再增加幾個知識性的問題，如：數(shù)軸上的點和平面直角坐標系內(nèi)的點在表示上有什么異同？已知點關(guān)于坐標軸對稱點的坐標與原坐標有何關(guān)系？能否在平面直角坐標系畫出一個邊長為4的正方形等問題，以幫助學生更全面、更完整地進行復(fù)習.

2 以圖理知：梳理知識網(wǎng)絡(luò)，構(gòu)建整體觀念

平時教學就像栽活一棵樹，單元復(fù)習好似育好一片林.栽活一棵樹容易，育好一片林要則要花更多功夫.單元復(fù)習不是老酒裝新瓶，而是要讓舊的知識帶來新的效率.2022年義務(wù)教育課程標準對課堂教學提出了新的要求，復(fù)習課堂更要體現(xiàn)新課程的理念，構(gòu)建知識的結(jié)構(gòu)化和整體性.因此，復(fù)習時不僅要引導(dǎo)學生通過“以問理知”實現(xiàn)對知識的全面回顧，更要促使學生理解各個知識點之間的內(nèi)在關(guān)聯(lián)，幫助學生將教材內(nèi)容進行歸類、綜合與整理，形成知識組合，建立整體結(jié)構(gòu).通過以圖理知的方式幫助學生構(gòu)建知識網(wǎng)絡(luò)，能夠促進學生的整體認知，帶動學生的單元學習觀念.

人教版教材每一單元的復(fù)習部分都設(shè)計了知識結(jié)構(gòu)圖，供師生復(fù)習時參考.圖1是《平面直角坐標系》一章的知識結(jié)構(gòu)圖(教材第83頁),從中可以清楚地了解本章的核心內(nèi)容：由確定點的位置引出平面直角坐標系的概念，再通過點的坐標來表示點的位置.除此之外 圖1中還滲透了知識學習的必要性和數(shù)學思想方法.從教材編排的教學內(nèi)容出發(fā)，也可以梳理出圖2所示的知識結(jié)構(gòu)圖，知道這一章學習幾節(jié)內(nèi)容、每節(jié)的主要內(nèi)容是什么，但這樣的圖示缺少知識之間的關(guān)聯(lián)性，也不能體現(xiàn)知識背后對數(shù)學思想和學習能力的教學要求.

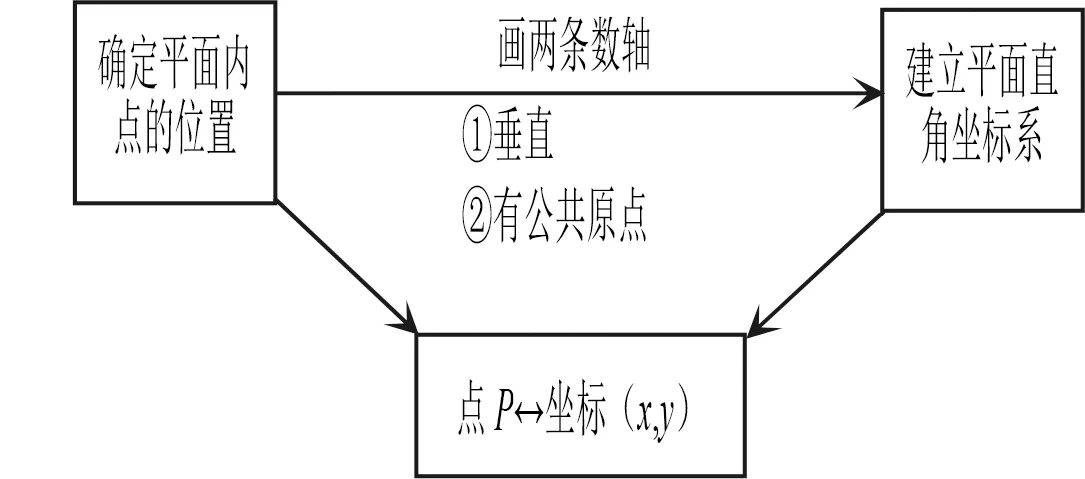
圖1

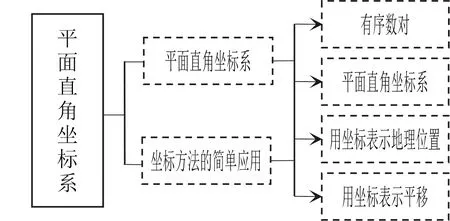
圖2

從復(fù)習的角度看，上述兩圖都略顯抽象和單薄，大部分學生只見森林而不識樹木.為了讓學生對細微的知識點有更清楚的了解，幫助學生將零散的知識串聯(lián)成網(wǎng)，以點帶面，提高復(fù)習效果，可以讓學生在復(fù)習時自己繪制知識網(wǎng)絡(luò)圖，把一系列的知識信息變成容易記憶的、有邏輯關(guān)系的圖畫，讓學生在梳理知識的同時理解知識結(jié)構(gòu)、明確知識關(guān)聯(lián)，實現(xiàn)復(fù)習的針對性和有效性.圖3和圖4是學生在本章復(fù)習時繪制的知識網(wǎng)絡(luò)圖，雖然邏輯關(guān)系稍有混亂，知識內(nèi)容不夠完整，但這樣的知識網(wǎng)絡(luò)圖有學生自主構(gòu)建和自我思考的過程，能夠體現(xiàn)學生在知識梳理和邏輯表達上的個性思考，有利于提高學生的記憶效果，形成整體學習觀念，培養(yǎng)學生的認知能力和思維能力.

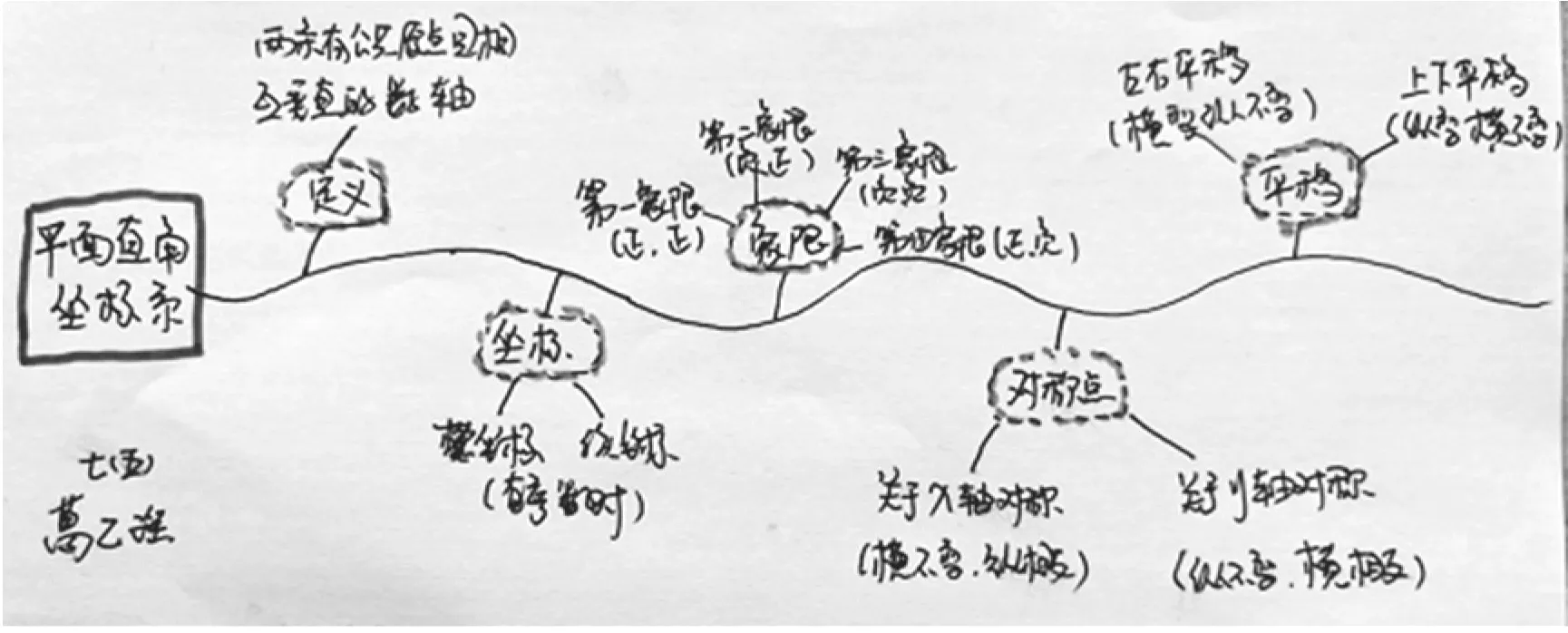
圖3

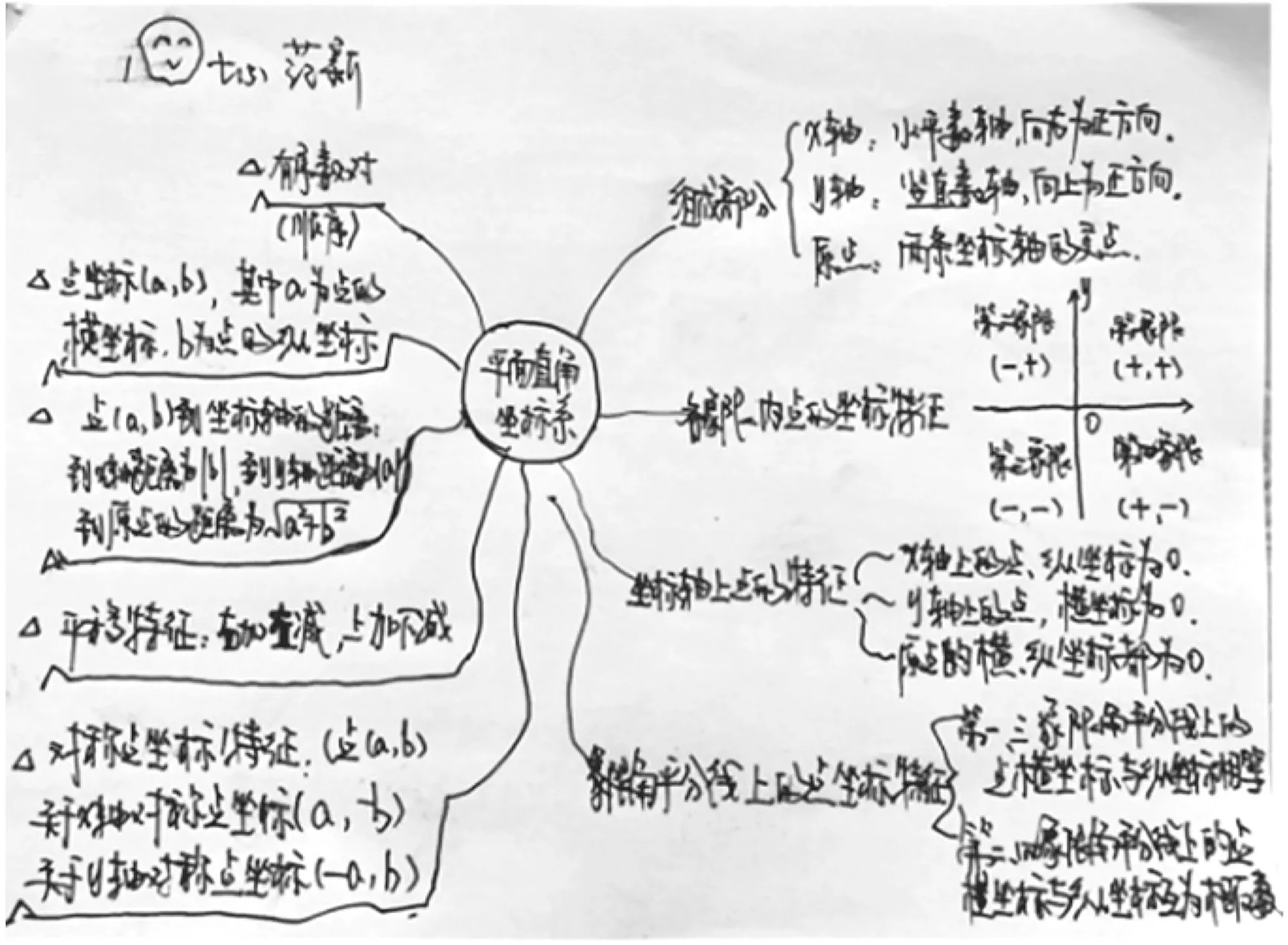
圖4

3 以題理知：剖析典型例題，提高應(yīng)用意識

以問理知喚醒學生對知識的回憶，以圖理知構(gòu)建知識的整體性和關(guān)聯(lián)性，但學以致用才能真正實現(xiàn)數(shù)學學習的應(yīng)用價值.數(shù)學家波利亞認為：中學數(shù)學教學首要的任務(wù)就是加強解題的訓(xùn)練.單元復(fù)習時可以通過對教材中典型例題或習題的再認識和再探究，更好地達成單元復(fù)習的目標.從解題中的“是什么”想到“為什么”，從“解題感悟”到歸納“思想方法”，這是一個自然的、合理的、科學的提升過程[2].美國教育心理學家加涅認為，任何一個學習過程都是有層次的，由簡單到復(fù)雜、由低級到高級排列而成.由于學生的學習存在主體差異性，因此單元復(fù)習的例題設(shè)計要緊密結(jié)合學情，遵循學生的認知規(guī)律，選擇更有典型性和知識性的例題，以幫助學生更好地回顧、梳理、重構(gòu)單元主題內(nèi)容.

(1)選題

平面直角坐標系這一章要注重學生從具體到抽象的能力培養(yǎng)，讓學生從數(shù)表示點坐標過渡到用字母表示點坐標，克服七年級學生對字母的生疏感和畏懼感，并利用坐標法解決相關(guān)問題.因此，我們需要選擇基礎(chǔ)性、典型性的例題，既要讓知識能夠有效聚焦，體現(xiàn)數(shù)學思想方法，又要讓學生感悟知識的應(yīng)用，實現(xiàn)能力的增長.教材第84頁第2題就是這樣的好題(圖5).

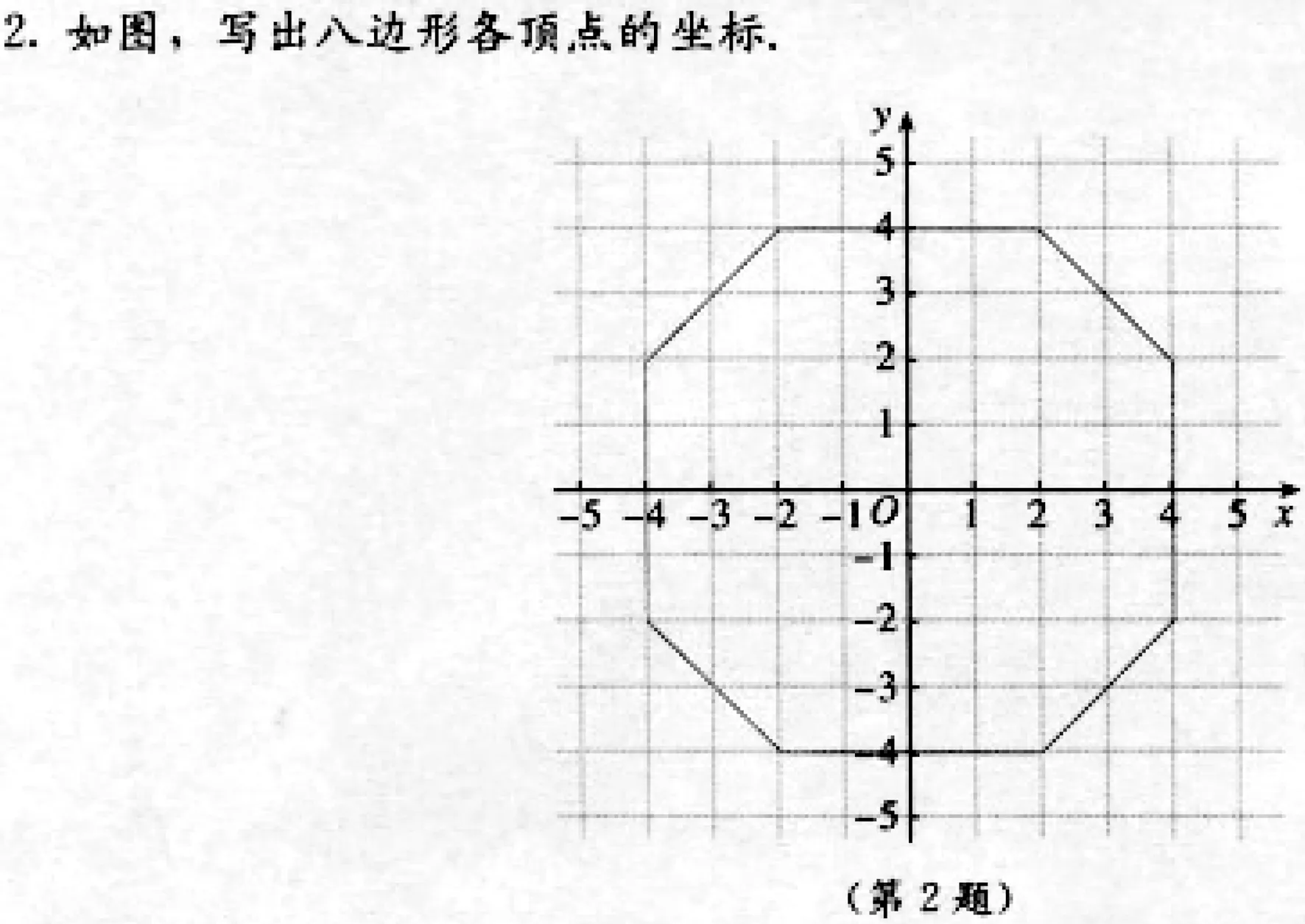
圖5

(2)講解

例題的選擇要能夠體現(xiàn)從特殊到一般、從簡單到復(fù)雜，兼顧不同學生的認知水平.復(fù)習課中的例題不能只講是什么，更要講為什么，也要培養(yǎng)學生問題解決的一般策略，逐步引導(dǎo)學生思考如何做、用什么方法做、為什么這么做、這一類問題怎么做.將題目的歸納提煉成解決問題的規(guī)律，有利于學生理清問題的本質(zhì)，提升學生的抽象意識和應(yīng)用能力.上述例題對于大部分學生來說是比較容易解決的，但從章節(jié)復(fù)習的視角看還是建議從問題入手，讓學生在思考與探究中喚醒與生長：①你能寫出這個多邊形的各個頂點坐標嗎？②坐標(2，4)和坐標(4，2)表示的是同一個點嗎？③這些頂點中哪些是關(guān)于坐標軸對稱的？④你能求出這個多邊形的面積嗎？⑤移動坐標系或者八邊形，點的坐標會發(fā)生變化嗎？ ⑥從題中你能夠感悟到哪些數(shù)學思想方法？你還能提出哪些與本圖形有關(guān)的問題等.經(jīng)典例題的價值就在于它的基礎(chǔ)性、應(yīng)用性和融合性，通過對以上幾個問題的思考，引導(dǎo)學生用數(shù)學的眼光觀察圖形、用數(shù)學的語言表達問題，全面提高學生的數(shù)學素養(yǎng).

(3)引申

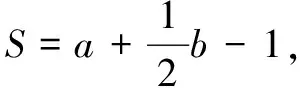
一個好的數(shù)學問題，除了結(jié)論具有知識性和應(yīng)用性，更需要有一定的推廣價值.皮克定理就具有這樣的推廣潛力，它可以推廣到更一般的多邊形，邊可以交叉，中間可以挖掉多邊形，還可以推廣到不同形式的格子點，甚至可以推廣到三維空間的多面體.這樣的引申重點不在于皮克定理是什么，而在于如何去發(fā)現(xiàn)、探索、猜想并證明一個定理，這才是學數(shù)學的重要方面.希望每位學生都不要只顧著解題與技巧，而忽略了數(shù)學結(jié)論背后那些精彩而又美麗的探索與發(fā)現(xiàn)的過程.

杜威提出：“教育就是已有經(jīng)驗的重組和再造，既能增加經(jīng)驗的意義，又能提高指導(dǎo)后來經(jīng)驗進程的能力.”新授課中單純的數(shù)學活動或單一的知識聯(lián)系，已不能再生數(shù)學經(jīng)驗，只有通過復(fù)習課將各個零散的知識和技能、方法和思想整合成一個系統(tǒng)，讓學生的知識建構(gòu)更全面、更系統(tǒng)，方法結(jié)構(gòu)更嚴密、更優(yōu)化，從而將知識與能力融為一體[1].從數(shù)學的本質(zhì)出發(fā)，深度挖掘教材復(fù)習資源，在抽象、邏輯推理和應(yīng)用中尋找復(fù)習的一般策略，能夠促進學生的深化和發(fā)展，提升學生的數(shù)學核心素養(yǎng).