構造函數法證明不等式的若干策略
2023-01-16 02:25:38浙江省奉化中學315503
中學數學研究(江西) 2023年2期
浙江省奉化中學 (315503) 張 園
運用對相關函數求導證明不等式是近年來高考命題的一類熱點題型,由于涉及許多導數問題中的解題技法,降低了解題的成功率,我們有不少同學都望而卻步.此類問題的破題關鍵就是找一個與待證不等式緊密聯系的函數,然后運用導數運算的方法,研究該函數的單調性、極值、值域等性質,進而達到證明不等式的目的.本文以近幾年高考題或模擬題為例,通過探索不同類型不等式的證明,闡述構造函數證明不等式的六種方法,供參考.
一、移項作差構造函數
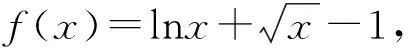
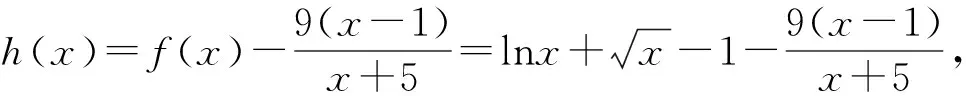
點評:移項作差法是證明不等式的最常用的方法,而構造新函數是利用導數解決問題的重要手段,本題中,在導函數式大小時根據解題需要又采用了放縮的辦法,并且再一次構造函數,最后才確定了大小關系,是一個難度較大的題目.
二、增添項后構造函數
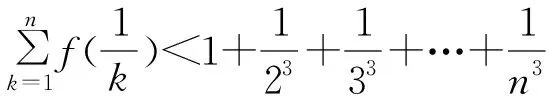

點評:通過將待證的結論式變形整理,揭露了待證式的實質,也就是需要證明不等式f(x) 點評:在本題中,由于是證明兩個變量的大小關系問題,通過換元,將兩元變換成一元,這樣降低了問題的難度,使之變成我們熟悉的、容易解決的問題了. 點評:在充分挖掘題目內涵的基礎上,將待證的不等式進行轉化、變形,使之等價變形為另一個大小關系證明的問題,然后再通過建立新函數輕松地解決了問題. 點評:由于待證的不等式比較復雜,在分析、化簡、變形的基礎上,再經過換元處理,成功的找到了同構關系,然后通過設新函數,這樣,成功地解決問題就是很容易了. 點評:在解題過程中,根據大小比較的需要,對表達式中的一部分采用構造函數處理,也是一個重要的解題思路,這種求解方法的關鍵是精確替換,以起作用、易解決為替換原則.三、及時換元后構造函數
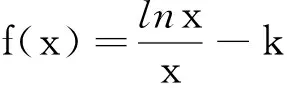
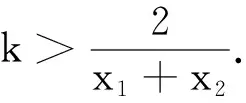
四、等價轉化后構造函數
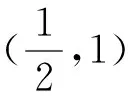
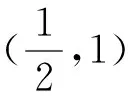
五、挖出同構關系后構造函數
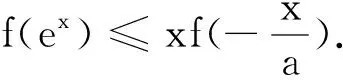
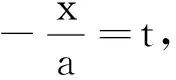
六、選擇關鍵部位構造函數
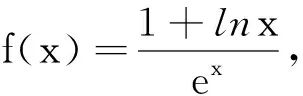
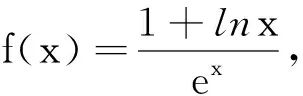
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中華詩詞(2020年1期)2020-09-21 09:24:52
小學生作文(中高年級適用)(2018年5期)2018-06-11 01:22:56
中學生數理化·七年級數學人教版(2017年11期)2017-04-23 07:18:00
數學大王·中高年級(2016年12期)2016-12-26 21:37:36
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34

