基于BB步長的一類原始-對偶算法①
鄭代秀
四川師范大學 數學科學學院, 成都 610066
對于帶線性等式約束的凸優化問題
min{f(x)|Ax-c=0}
(1)

ALM算法本質上是一類原始-對偶算法,更新乘子λ的過程本質上是用梯度法求解對偶問題,其中參數ρ是梯度算法的下降步長.而在優化問題的梯度類算法中,Barzilai-Borwein算法(以下簡記為BB算法[8])的表現比較好(具有擬牛頓性質).所以可以考慮用BB算法的步長去替代ALM中固定步長ρ, 得到一個新的凸優化問題的原始-對偶算法,我們將其簡記為ALM-BB算法.該思想首先由文獻[9]在研究大數值優化問題的乘子交替方向法[10-11]的改進型算法時提出,但沒給出算法的收斂性證明.本文在目標函數f為強凸二次函數,約束函數中矩陣A行滿秩的條件下證明了ALM-BB算法收斂性.
范數最優控制問題本質上是無窮維的二次凸優化問題,通過適當的離散格式可以獲得其有限維框架的近似問題,且其近似問題為一類二次凸優化問題.由此可以利用本文的算法進行數值求解.通過求解范數最優控制問題的數值算例發現,ALM-BB算法收斂速度更快.
本文的結構如下: 在第1節中給出一些記號和預備知識; 在第2節中介紹ALM-BB算法并證明其收斂性; 在第3節中給出范數最優控制的離散格式,并利用實際算例說明ALM-BB算法的有效性; 在第4節中作總結.
1 預備知識
考慮如下二次凸優化問題:
s. t.Ax-c=0
(P)
其中S∈Rn×n,b∈Rn,c∈Rm,A∈Rm×n.在本文中,我們作出如下假設:
(A1)S∈Rn×n為對稱正定矩陣;
(A2) rank(A)=m.

向量λ稱為對偶變量或者原問題(P)的Lagrange乘子向量.
Lagrange對偶函數定義為
問題(P)的對偶問題定義為
(D)
引理1[2]對于凸優化問題(P),若條件(A1)-(A2)成立,那么x*,λ*分別是原、對偶問題的全局最優解當且僅當
(2)
稱滿足(2)式的(x*,λ*)為KKT對. 由引理1知求解凸優化問題(P)的KKT對等價于求解原問題與對偶問題的最優解.
優化問題(P)的增廣Lagrange函數為:
(3)
其中ρ>0是罰參數. 同樣,可利用其增廣Lagrange函數定義對偶函數:
引理2[12]若x*,λ*分別為增廣Lagrange函數Lρ(x,λ)對應的原始、對偶問題的解,則(x*,λ*)為Lagrange函數L(x,λ)的KKT對.
下面我們回顧經典的增廣Lagrange乘子算法.求解問題(P)的增廣Lagrange乘子法(ALM)的迭代格式如下:

算法1: ALM1. 給定初始點x0與λ0, ρ>0, 終止誤差ε, 令k=0; 2. 計算xk+1=arg minx∈RnLρ(x, λk); 3. 若‖Axk+1-c‖<ε, 停止; 否則轉第4步; 4. 計算λk+1=λk-ρ(Axk+1-c); 5. 令k=k+1, 轉第2步.
該算法中的步長ρ是固定的,而罰參數若選取不當,會顯著增加求解時間.為改進算法,考慮用BB算法的步長αBB去替代固定的步長ρ.給定xk,xk-1,λk,λk-1, 定義
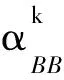

算法2: ALM-BB1. 給定初始點x0與λ0, ρ>0, 終止誤差ε, 令k=0; 2. 計算xk+1=arg minx∈RnLρ(x, λk); 3. 若‖Axk+1-c‖<ε, 停止; 否則轉第4步;4. 若k=0, 計算λ1=λ0-ρ(Ax1-c); 否則計算λk+1=λk-αkBB(Axk+1-c); 5. 令k=k+1, 轉第2步.
2 ALM-BB算法的收斂性
在本節,我們證明算法2的收斂性.首先, 我們證明算法2中更新Lagrange乘子的過程等價于求增廣Lagrange函數對應的對偶問題的BB算法.
定理1若條件(A1)-(A2)成立,則算法2中更新Lagrange乘子的過程等價于求增廣Lagrange函數對應的對偶問題的BB算法.
證由條件(A1),對任意給定的λ∈Rm,存在唯一的x∈Rn使得
dρ(λ)=Lρ(x,λ)

xLρ(x,λ)=Sx-b-ATλ+ρAT(Ax-c)=0
由此可得x的顯式表達式:
x=R-1ATλ+R-1h
其中R=S+ρATA,h=ρATc+b. 因此對偶函數
(4)
其中C為與x,λ無關的常數項.
由(4)式,增廣Lagrange函數對應的對偶問題可寫為如下無約束凸二次優化問題(為簡單起見,我們將常數項C省略,它對對偶問題最優解的求解不會產生影響):
(5)
在假設條件(A1)-(A2)下,矩陣AR-1AT是對稱正定矩陣,因此優化問題(5)的解存在唯一.
由文獻[8],求解無約束凸優化問題(5)的BB算法迭代格式為
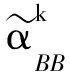
(6)
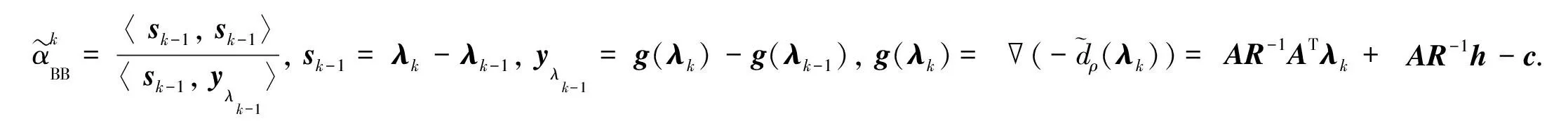
在ALM-BB算法第2步中,利用凸優化問題的一階最優性條件可得xk+1的精確解為
xk+1=R-1ATλk+R-1h
(7)
將(7)式代入ALM-BB算法第3步, 則有
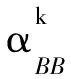
對比算法2與對偶問題的BB算法,我們只需證明
其中xk+1為算法2中求得的子問題的最優解.
事實上,由凸優化問題的一階最優性條件可知xk+1應滿足
xLρ(xk+1,λk)=Sxk+1-b-ATλk+ρAT(Axk+1-c)=0
利用之前的記號可得
xx+1=R-1ATλk+R-1h
(8)
下面我們利用BB算法的收斂性結果證明算法2產生的迭代序列的收斂性.
定理2設條件(A1)-(A2)成立,則由算法2得到的迭代序列{(xk,λk)}收斂到原問題的KKT對(x*,λ*).特別地,x*為原問題的最優解.
證由條件(A1)-(A2)知x*為原問題的最優解等價于存在λ*使得(x*,λ*)為KKT對,即(x*,λ*) 滿足

(9)

x*=R-1ATλ*+R-1h
(10)
結合(9)式和(10)式可得
Ax*=AR-1ATλ*+AR-1h=c
即(x*,λ*)滿足條件λL(x*,λ*)=0.
進一步,
(11)
由(10)式和(11)式可得
xL(x*,λ*)=R(R-1ATλ*+R-1h)-ATλ*-h=0
故(x*,λ*)為原問題的KKT對.
此外,利用BB算法的R-線性收斂率, 知ALM-BB也具有R-線性收斂率.
3 范數最優控制問題及其離散格式
設T>0,Rn與Rm分別為n維與m維歐式空間,考慮如下線性控制系統:
(12)
其中:A∈Rn×n,B∈Rn×m;x(·)為系統的狀態,u(·)為系統的控制,x0∈Rn是給定的初值,xT∈Rn為給定的終值. 稱x(T)=xT為終端狀態約束.定義性能指標:
由臨時仰拱臺階法沿高鐵盾構隧道方向地表沉降曲線圖9可以看出,地表最大沉降位于地鐵雙區間隧道中心截面,越靠近中心施工引起變形疊加效應越明顯,遠離中心后疊加效應逐漸降低,在距地鐵雙區間中心截面20 m附近存在反彎點,隨后地層變形主要受單線隧道施工影響。
(13)

(14)
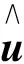
下面,我們給出范數最優控制問題(14)的離散格式.對控制系統(12)中的線性微分方程,我們有x(T)的顯示表達式:

記η=eATx0,M(t)=eA(T-t)B.則狀態約束可表示為:

(15)
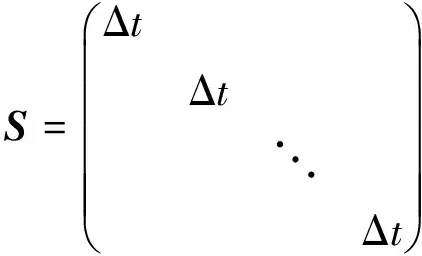
將(15)式中的積分表達式采用分段常量的逼近策略,取
M(t)=M(ti),t∈[ti,ti-1),i=0,1,…,N-1
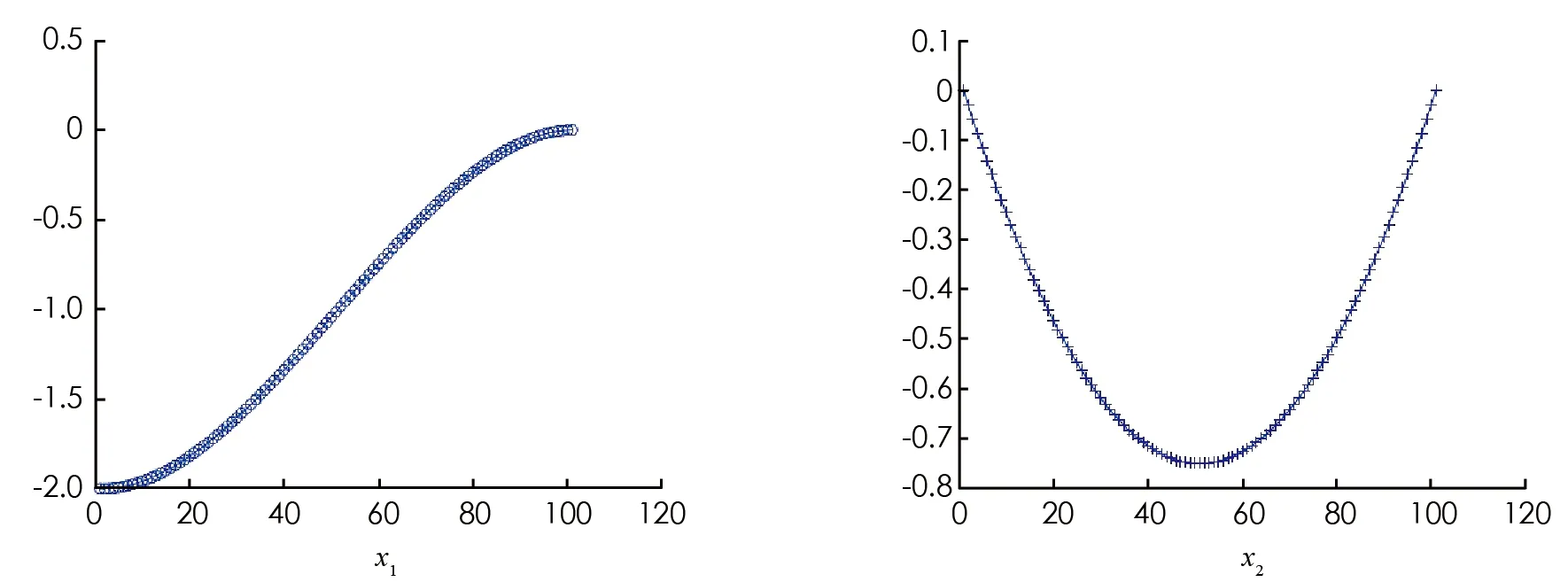
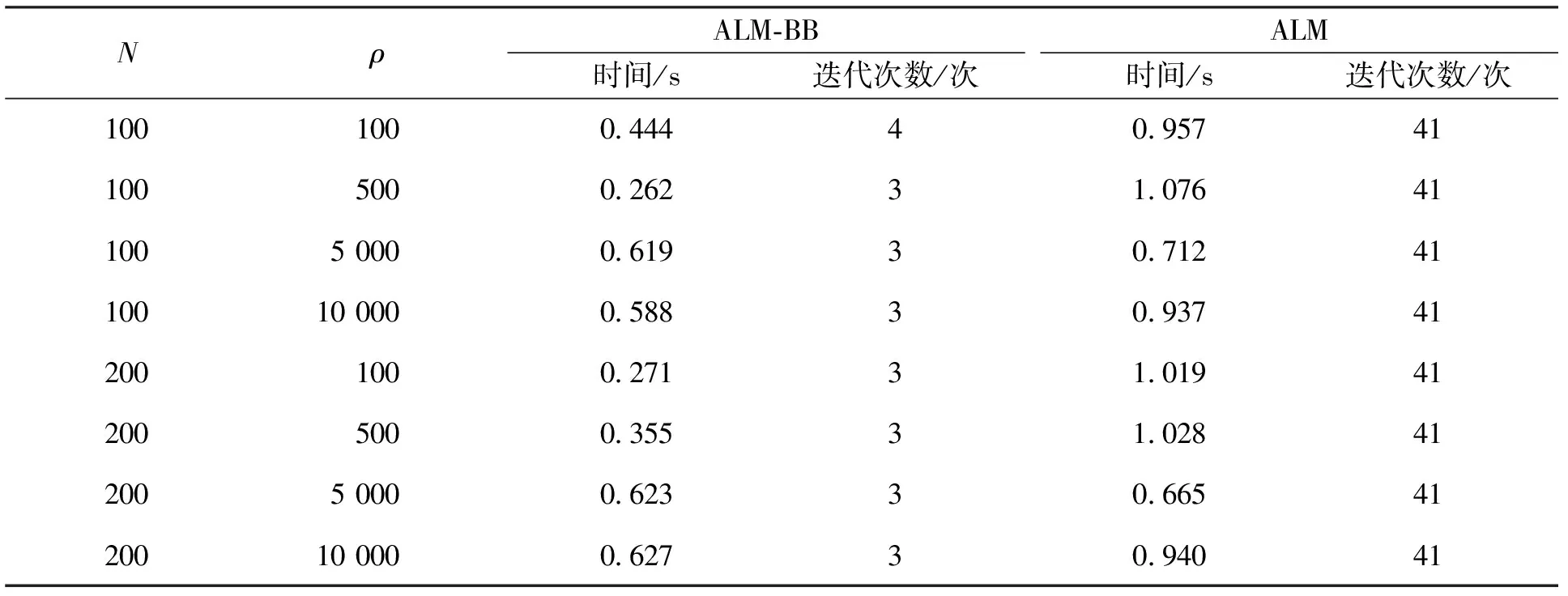
其中0=t0 可得如下近似方程: 若記u=(uT(t0),uT(t1), …,uT(tN-1))T. 在適當的可積性條件下,可得: 其中 由此可得,范數最優控制問題(12)對應的離散優化問題為: s.t.Mu+c=0 (16) 其中 我們對線性系統(12)作如下假設. (A3)線性系統(12)完全能控,即秩條件rank(A,BA, …,Bn-1A)=n成立. 在條件(A3)下,最優控制問題(14)解存在唯一,并且其離散優化問題(16)中的矩陣S,M滿足假設條件(A1)-(A2). 其中C為常數. 由引理3,求原范數最優控制問題(14)可轉化為求凸優化問題(16). 進一步,在假設條件(A3)下,我們可用ALM-BB算法求解問題(16). 下面我們給出一個具體的算例,并用它對原始的ALM與ALM-BB算法進行比較. 例6設T=3,n=2,m=1,考慮如下控制系統: 及性能指標 圖1 最優狀態圖 為了說明ALM-BB算法的有效性, 我們選擇不同的罰參數和劃分細度進行計算, 將ALM-BB和ALM算法的計算時間和迭代次數對比見表1. 表1 ALM-BB與ALM數值實驗結果對比 由表1可以看出, 在劃分細度與罰參數相同的情況下, ALB-BB算法迭代步數更少, 收斂速度更快. 但是當罰參數選取過大時, ALM與ALM-BB算法運行時間差別不大, 對罰參數的選取依然敏感. 本文通過改變ALM算法中更新乘子這一迭代步的步長來提高算法的收斂速度. 范數最優控制問題本質上是無窮維的二次凸優化問題, 通過適當的離散格式可以將其轉為有限維的二次凸優化問題. 通過求解范數最優控制問題的數值算例發現, ALM-BB算法較ALM計算效率更高. 從數值實驗看出ALM-BB算法的數值表現仍依賴于參數的選取. 此外, 本文的收斂性證明依賴于凸二次規劃問題的具體結構以及子問題可精確求解, 對于更一般的非精確的ALM-BB算法的收斂性有待進一步研究.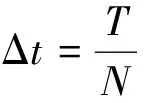
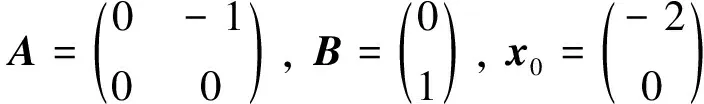
4 總結

