基于生成模型的塊稀疏偏差建模①
斯那雨追,余鵬彬,王建軍
西南大學 數學與統計學院, 重慶 400715
傳統的信號采樣方式是基于Nyquist采樣框架實現的, 根據香農采樣定理, 若要從采樣的離散信號中無失真地恢復模擬信號, 則要求采樣速率必須達到信號帶寬的兩倍以上[1-2]. 然而, 在現實世界中, 信號采集的成本很高. 為了解決這一問題, 文獻[3]提出了壓縮感知理論, 其核心思想是將壓縮與采樣相結合, 突破了香農采樣定理的瓶頸, 使得高分辨率信號的采集成為可能. 從數學角度出發, 壓縮感知的核心思想為一個線性測量過程. 選取測量矩陣A∈Rm×n(m?n), 可以得到信號x的測量信號y. 數學表達式如下:
y=Ax+ε
(1)
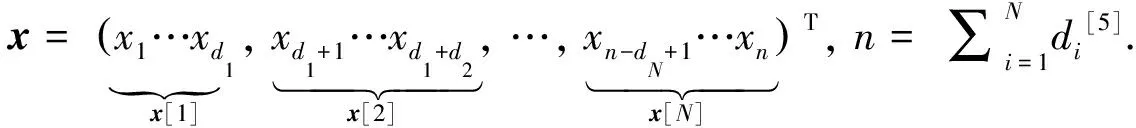
為了使得欠定方程有唯一解, 即便是在無噪聲的情況下, 通常需要對未知向量x進行一些結構性假設, 最常見的結構性假設是x是稀疏的. 如果信號在某一個正交空間具有稀疏性, 就能以較低的頻率采樣該信號, 并可能以高概率精確重建該信號. 經典的變換方法包括離散余弦變換(DCT)[8]、傅里葉變換(FFT)[9]、離散小波變換(DWT)[10]等. 在上述環境中, 如果矩陣A滿足某些條件, 如限制等距性質(RIP)[11]或限制特征值條件(REC)[12], 則可以保證x從y中有效恢復.
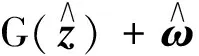
s.t.A(G(z)+ω)=y
(2)
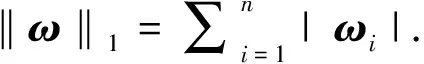
在本文中, 我們研究了基于生成模型的壓縮感知塊稀疏偏差模型. 在該方法中, 我們使用2.1范數來約束偏差向量, 其中G: RkRn是生成函數,ω∈Rn,A∈Rm×n是測量矩陣,y∈Rm是觀測向量. 本文關心的模型是
s.t.A(G(z)+ω)=y
(3)
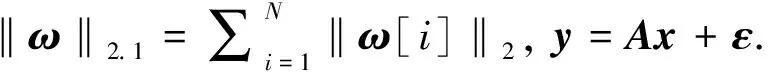
(4)
其中λ是拉格朗日常數. 我們給出了理論結果和仿真, 在理論上, 本文首先提出了針對塊稀疏信號的塊約束等距性質(B-RIP)和塊有限等距性質(B-S-REC), 如果測量矩陣具有這兩個性質, 則最優解碼的重構誤差存在上界. 最后推導出在生成函數條件下以高概率成功恢復所需的測量次數. 在實驗方面, 為了進一步驗證本文提出的Block Sparse-Gen的有效性和優越性, 使用兩個數據集(MNIST和CelebA)和兩個生成模型(VAE和DCGAN)進行了一系列實驗. 在測量次數相對較少的情況下, 該方法的重建誤差遠小于基于LASSO的恢復、基于生成模型的恢復和稀疏生成.
1 相關定義
定義1BS(0)={x: ‖x-0‖2.0≤l}, 其中
定義2(Block-RIP)對于參數α∈(0, 1) 和一個給定的分塊τ={τ1,τ2, …,τN}, 如果對于所有的x∈BS(0)滿足下面的不等式, 則我們說矩陣A∈Rm×n滿足B-RIP(,α),
(5)
定義3(Block-REC)對于參數γ>0和一個給定的分塊τ={τ1,τ2, …,τN}, 如果對于所有的x∈BS(0)滿足下面的不等式, 則我們說矩陣A∈Rm×n滿足B-REC(,γ),
‖Ax‖2≥γ‖x‖2
(6)
定義4(Block-S-REC)令S?Rn, 對于參數γ>0,δ≥0和一個給定的分塊τ={τ1,τ2, …,τN}, 如果對于所有的x1,x2∈S滿足下面的不等式, 則我們說矩陣A∈Rm×n滿足B-S-REC(S,γ,δ),
‖A(x1-x2)‖2≥γ‖x1-x2‖2-δ
(7)
2 主要結論及證明
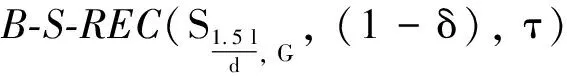
(8)
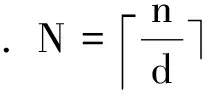
為了證明引理1, 首先定義如下記號. 考慮到要在我們的分析中考慮測量噪聲, 我們將矩陣A的ε型管集定義為
TA(ε)={ω: ‖Aω‖2≤ε}
(9)

(10)
記
(11)
為了證明引理1, 我們先陳述并證明下面的引理2和引理3.

(12)
對于某些給定的常數C0,τ,t≥0. 這樣的解碼器存在的充分條件由下式給出
(13)

(14)
(15)
這意味著
x-Δ(Ax+ε)∈TA(2εmax)
結合混合范數空間屬性, 我們有
(16)

(17)
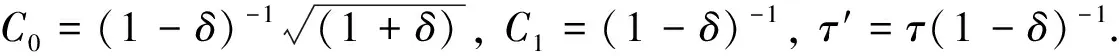
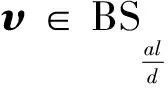
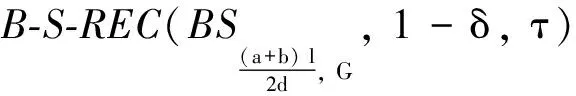
(18)
可以將η寫為η=ηT+ηT2+…+ηTs. 再根據η∈TA(ε), 將AηT表達為AηT=-A(ηT2+…+ηTs)+γ, 其中‖γ‖2≤ε. 因此,
(19)
根據(18),(19)兩個不等式可以得到
(20)
在兩邊加上‖η′Tc‖2并根據三角不等式可以得到
(21)

(22)
結合(21)式可得
(23)
引理1的證明結合引理2和引理3, 令a=2,b=1, 我們可以直接推導出引理1.

(24)

為了證明引理4, 我們先闡述下面的引理5和引理6.
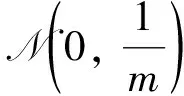
(25)
則A至少以1-e-Ω(δ2m)的概率滿足B-RIP(l,δ) .
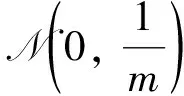
(26)
則A至少以1-e-Ω(δ2m)的概率滿足B-S-REC(G(Bk(r)),1-δ,τ) .
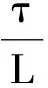
(27)
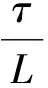
‖G(z1)-G(z′1)‖2≤τ
‖G(z2)-G(z′2)‖2≤τ
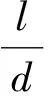
(28)
再次由三角不等式, 可以得到
(29)
由文獻[13]引理8.3, 我們有以概率1-e-Ω(m)滿足
‖AG(z′1)-AG(z1)‖2=O(τ)
‖AG(z2)-AG(z′2)‖2=O(τ)
將這一事實應用于(29)式, 則可以得到
‖AG(z′1)-AG(z′2)+Aυ‖2≤‖AG(z1)-AG(z2)+Aυ‖2+O(τ)
(30)
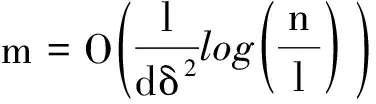
(1-δ)‖G(z′1)-G(z′2)+υ‖2≤‖AG(z′1)-AG(z′2)+Aυ‖2
(31)
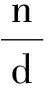
(32)
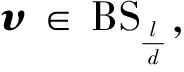
(33)
以下不等式
(1-δ)‖G(z1)-G(z2)+υ‖2≤‖A(G(z1)-G(z2)+υ)‖2+O(τ)
(34)
至少以1-e-Ω(δ2m)的概率成立. 引理4得證.
結合引理1和引理4, 我們可以得到如下所述定理1的結果.

(35)
假設Δ是滿足引理1的解碼器, 則我們至少以1-e-Ω(δ2m)的概率有
(36)
對于任意的x∈Rn, ‖ε‖2≤εmax, 其中C0,C1,γ,τ′的定義參見引理1.
3 實驗
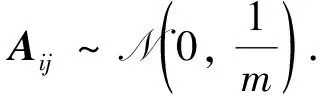
3.1 實驗設置
MNIST數據集中每個圖像的大小為28×28像素, 并且每個像素值為0或者1. 對于這個數據集, 我們根據Block Sparse-Gen 來訓練VAE, 以恢復原始圖像. 由于圖像包含單個通道, 因此輸入尺寸為28×28=784, 學習率為0.1,λ=0.1. 在CelebA數據集中, 將人臉圖像裁剪為64×64像素大小, 使每個圖像輸入的尺寸為64×64×3=12 288, 并將每個像素值縮放為[-1, 1]. 對于這個數據集, 考慮根據Block Sparse-Gen模型訓練一個DCGAN來恢復原始圖像, 同時會將結果與其他模型和算法進行比較. 對于Block Sparse-VAE, 使用LASSO作為基準, 并將其與基于生成模型的算法(VAE)和添加了稀疏偏差的生成模型(Sparse-VAE)進行比較. 對于Block Sparse-DCGAN, 我們將結果與LASSO的結果進行了比較, LASSO的結果包含兩個變換域: 二維離散余弦變換和小波變換. 類似地, 還將結果與基于生成模型的算法(DCGAN)和添加了稀疏偏差的生成模型(Sparse-DCGAN)進行比較.
3.2 重建結果
為了探索每種算法的重建效果, 對于MNIST數據集, 我們在圖1展示重建的均方誤差結果. 可以看出, 與理論結果類似, 隨著采樣數的增加, 均方誤差明顯減少, 并且Block Sparse-VAE模型相比其他的模型能夠更可靠地重構未知樣本. 類似地, 我們給出了CelebA數據集的恢復結果, 如圖2所示. 與MNIST數據集類似, 本文算法明顯優于LASSO等模型. 尤其是當測量次數較少時, 具有獨到的優勢. 圖3和圖4展示了MNIST數據集在測量次數為80時的恢復效果以及CelebA數據集在測量次數為1 000時的恢復效果. 我們發現除LASSO外, 其他方法恢復效果明顯較好. 這足以說明一個與理論一致的結果, 即在測量次數較少的情況下, 基于生成模型的恢復方法的強先驗完全優于基于LASSO的稀疏向量恢復方法. 另外可以發現我們提出模型的恢復效果優于其他的模型, 顯示了所提分塊方法的有效性和優越性.
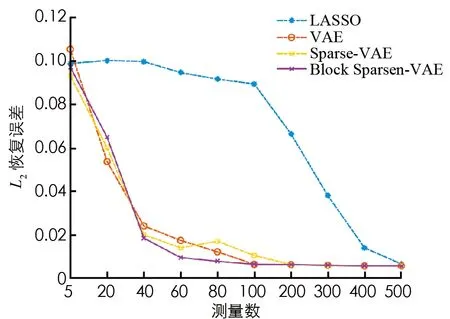
圖1 MNIST
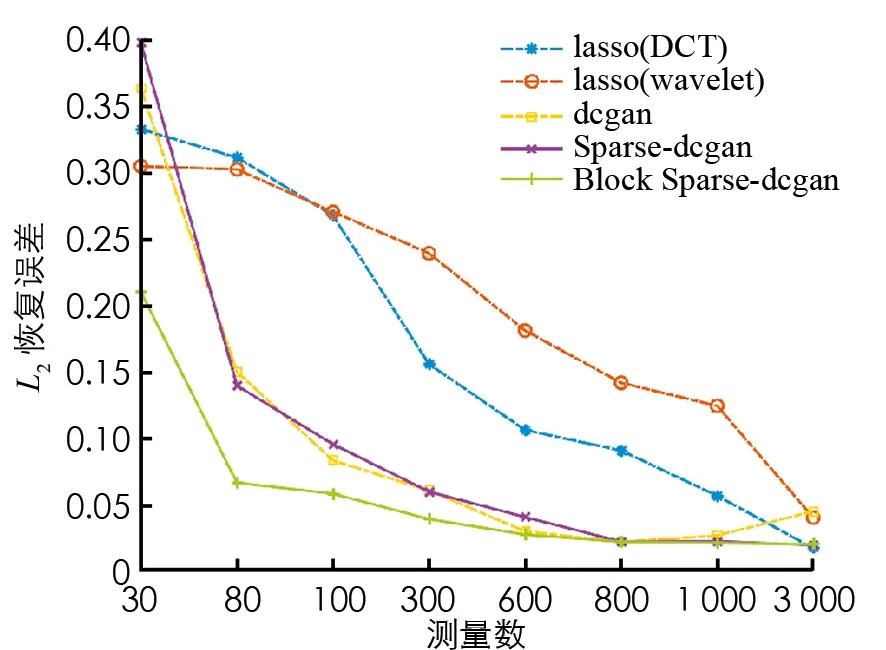
圖2 CelebA

圖3 MNIST數據集恢復效果(m=80)

圖4 CelebA數據集恢復效果(m=1 000)
4 結論
本文對基于生成模型的稀疏偏差建模進行了推廣, 提出了Block-Sparse Gen模型. 針對此模型, 我們提出了Block-S-REC條件, 結合Block-RIP條件推導了在生成函數的稀疏偏差范圍內最優解碼器的誤差上界, 并給出了原始信號高概率有效恢復的測量值次數
此結果在d=1時退化為稀疏生成(Sparse-Gen)的情況. 在數值實驗中, 我們提出的模型減少了成功恢復的測量值條件, 提高了恢復效果.

