溫度場的有限差分計算
——以一維溫度場為例①

趙銳，楊名揚，淡丹輝，3

1.新疆大學 建筑工程學院， 烏魯木齊 830017； 2.新疆建筑結構與抗震重點實驗室， 烏魯木齊 830017； 3.同濟大學 橋梁工程系， 上海 200092

熱量的傳遞過程是通過熱傳導、熱對流和熱輻射3種方式進行的， 其中， 熱傳導是通過固體或者靜止流體傳播熱量； 熱對流局限于液體和氣體， 并且往往涉及流體固體邊界的熱交換； 熱輻射能量是通過電磁波傳遞的[1]. 在計算物體溫度場時， 固態物體內部熱量的傳遞方式為熱傳導， 將熱對流和熱輻射作為邊界條件. 分析傳熱問題時， 從不同的角度出發可將傳熱問題分為3類： ①根據熱量傳遞的維度可將熱傳導問題分為一維熱傳導問題、二維熱傳導問題和三維熱傳導問題； ②根據是否考慮溫度場隨時間變化， 可分為瞬態溫度場和穩態溫度場； ③根據是否考慮材料性能隨溫度的變化， 可分為變系數熱傳導問題和常系數熱傳導問題.

熱量傳遞引起的溫度場變化涉及到生物[2]、醫療[3]、材料[4-6]， 建筑結構[7-9]等多個領域， 在溫度場研究中， 將與溫度分布相關的物理參數稱為熱工參數， 包括比熱、熱傳導系數以及密度， 其中密度隨溫度變化微小. 對于特殊材料或環境溫度變化范圍較小的情況， 如自然環境等， 可不考慮材料熱工參數隨溫度的變化. 然而， 大多材料的熱工參數都會隨著溫度的變化而改變， 以鋼材為例， 各國規范均給出了鋼材熱工參數隨溫度的變化規律[10]. 為了求解熱工參數隨溫度變化的熱傳導問題， 國內外學者做了大量研究. 在穩態溫度場的研究中， ünal[11]基于平面板模型提出一種考慮熱傳導率隨溫度線性變化的一維穩態熱傳導問題求解方法； Hussein[12]通過理論推導， 在球坐標系中求解了實心球體在有內部熱源、考慮材料熱傳導率隨溫度線性變化的情況下的一維穩態傳熱問題， 并且對比了使用3種不同材料時的溫度分布情況； 高仲儀[13]采用λ變換法求解變系數穩態熱傳導問題， 該方法假設熱傳導率隨溫度線性變化且熱傳導率與溫度一一對應， 將溫度逆向表示為熱傳導率的函數， 通過求解熱傳導率進而得到溫度場； 嚴治軍[14]給出了具有對流換熱邊界條件的一維常系數熱傳導差分解法， 考慮多層不同材料時溫度場分布， 最后采用FORTRAN語言編制成熱傳導解析的計算程序. 瞬態溫度場的研究也大多是基于一定假設簡化得到的計算結果， 魏光坪[15]、康為江[16]和彭友松[17]在研究自然條件下的橋梁溫度場時， 由于自然環境下溫度變化較小， 通常將材料熱工參數視為常數， 考慮了3種熱傳遞方式對結構溫度場的影響； 李國強等[18]在對火災下二維鋼板-混凝土組合樓板溫度場分析時， 考慮結構的熱對流和熱輻射邊界條件， 并探究火災位置和分布對樓板溫度場的影響， 通過對結果進行參數分析， 提出了適用于火災下的樓板溫度計算的簡化公式； 胡克旭等[19]采用有限單元法， 假定單元溫度隨著位置坐標線性變化， 計算了火災下壓型鋼板-混凝土組合樓板在存在熱對流和熱輻射， 同時考慮建筑材料熱工參數隨溫度變化時的溫度場.

實際上， 由于材料比熱和熱傳導率均會隨著溫度變化， 加之邊界條件的復雜性， 使得求解偏微分方程得出解析解是極少數情況. 采用數值方法計算， 能有效簡化計算過程. 常見的數值解法有有限元法、有限體積法、邊界元法和有限差分法等， 這些方法中， 有限差分法具有簡單且穩定的優點[20]. 本研究基于熱傳導的有限差分方程， 使用MATLAB編程計算結構溫度場. 以簡化的一維變系數瞬態溫度場分布模型為例， 闡明考慮材料熱工參數隨溫度變化時的有限差分法計算過程， 并建立有限元模型進行結果驗證.

1 熱傳導差分方程的建立

理論推導求解物體溫度場一般采用解析法和數值法. 其中， 解析法是以熱傳導方程為基礎， 求解偏微分方程， 尋求物體溫度分布與時間和位置關系的函數表達式， 即T(x，y，z，t). 實際能采用解析法求解的熱傳導問題是極少數情況， 因此， 通常采用有限差分的數值方法建立傳熱的有限差分方程， 求解溫度場近似值[21]， 通過減小單元格大小(時間步長、空間步長)來提高計算精度.

有限差分方程的建立可通過兩種方式完成： 一是基于熱傳導方程建立差分方程， 二是基于能量平衡建立差分方程.

1.1 基于熱傳導方程的差分方程

熱傳導方程為：

(1)

式中：λ(T)為熱傳導率；ρ為材料密度；C(T)為比熱容.(1)式表達了溫度在空間上的分布與溫度隨時間變化的關系：

基于熱傳導方程建立傳熱的差分方程， 就是以熱傳導方程為基礎， 用差分代替微分， 將偏導寫成差分形式進行求解. 對于任意連續函數， 使用泰勒級數將x0相鄰兩點函數值f(x-1)和f(x1)在x0處展開得：

(2)

(3)

(2)式+(3)式得到f(x)在x0處沿著x方向二階導數， 略去高階項， 得到：

(4)

同理， 在圖1所示三維直角坐標系中， 與點P(x0，y0，z0)相鄰的上下左右前后6個點的溫度值分別為TU，TD，TL，TR，TF，TB.

圖1 空間位置示意

則T(x，y，z)在點P(x0，y0，z0)處各方向二階偏導可表示為：

(5)

取空間間隔Δx=Δy=Δz=Δ， 時間間隔為Δt， 時間偏導采用向前差分格式則有：

(6)

式中：T′為P點下一時刻溫度值.將(5)式和(6)式帶入(1)式中， 得到基于熱傳導方程的差分方程， 整理得：

(7)

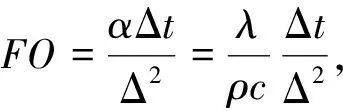
(8)

1.2 基于能量平衡的差分方程

基于能量平衡建立差分方程， 是根據單元能量平衡的思想進行的， 即： 單元內輸入熱量和輸出熱量的差值， 引起單元溫度變化. 差值為正， 單元溫度升高； 差值為負， 單元溫度降低.

在圖2所示三維空間直角坐標系中取控制單元(圖3).

圖2 空間直角坐標

圖3 控制單元示意

圖2中A為外界節點(邊界條件)，P1為邊界節點，P2為中間節點. 圖3中， 與點P相鄰的6個點U，D，L，R，F，B分別代表點P上下左右前后相鄰點. 為簡化計算， 令網格間隔Δx=Δy=Δz=Δ， 因此相鄰各點到P的距離均為Δ. 節點i到相鄰節點j之間的傳熱系數為Kij， 基于傅里葉定律， 從節點j到i的熱量為[13]：

Qij=Kij(Tj-Ti)

(9)

單元內蓄積的能量使得單元內部溫度發生變化， 節點i的能量平衡方程為：

(10)

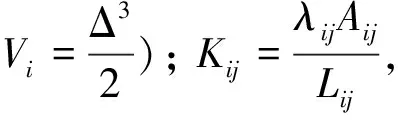
圖3中， 中間節點

(11)

圖2中， 邊界節點(假設為左側邊界， 右側同理)

(12)

(13)

對(12)式右側進行向前差分， 左側采用加權平均的形式， 整理得：

(14)

式中， 若β=0， 方程為顯式格式；β=1， 方程為隱式格式. 得到差分方程， 結合相應的邊界條件即可得到溫度場分布.

1.3 差分方程的特殊形式

實際情況中多為三維熱傳導問題. 但在處理一些特定問題時， 適當做出假設， 可將三維簡化為二維或一維情況.

按照1.2節思路， 可得二維熱傳導差分方程為：

(15)

一維熱傳導差分方程為：

(16)

同于1.1節， 若β=0， 方程為顯式格式；β=1， 方程為隱式格式.

1.4 顯示差分的穩定性要求

對于顯式格式的有限差分方程， 在計算時， 涉及到方程的穩定性問題.

令式(14)中β=0， 得顯式格式差分方程：

(17)

由(17)式可知， 由于FO>0， 所以當T的系數(1/FO-6)<0時，T越大T′ 就會越小， 即此時刻溫度越大下一時刻的溫度越小， 顯然違背熱力學原理. 因此， (1/FO-6)≥0同理. 對于二維和一維有相同的約束.

內部節點：

一維直角坐標FO≤1/2

二維直角坐標FO≤1/4

三維直角坐標FO≤1/6

(18)

邊界節點(對流邊界條件)：

一維直角坐標FO≤1/[2(1+Bi)]

二維直角坐標FO≤1/[2(2+Bi)]

三維直角坐標FO≤1/[2(3+Bi)]

(19)

式中：Bi=hΔ/λ， 時間步長限制取(18)式與(19)式所得交集. 在一維直角坐標系中， 由(19)式可得時間步長限制為：

(20)

2 差分方程求解

以“一維無熱源具有熱對流邊界條件的熱傳導問題”為例， 分別介紹是否考慮材料熱工參數隨溫度變化兩種情況時的溫度場求解方法.

已知初始時刻所有節點溫度均為T(X， 0)=T0； 左邊界環境溫度滿足TA=A(t)， 右邊界環境溫度滿足TB=B(t)， 表面傳熱系數為hw. 將構件沿x方向均勻劃分為N個單元格(圖4).

圖4 單元劃分示意

2.1 常系數熱傳導方程

在上述一維熱傳導問題中， 取T(X， 0)=T0=20 ℃， 左側環境溫度取國際標準升溫曲線(ISO834)[14]溫度值A(t)=20+345lg(8t+1)，B(t)=20 ℃，L=4 m，N=80. 熱工參數見表1.

表1 熱傳導相關參數值

對于常系數熱傳導問題， 采用顯式和隱式格式均可求解. 由(13)式和(16)式得節點i的差分方程， 其中顯式差分格式為：

(21)

隱式差分格式為：

(22)

2.1.1 常系數顯式求解

采用顯式格式求解熱傳導問題時， 首先根據精度要求， 選取空間網格Δ大小， 再根據顯式格式的穩定性要求確定時間步長Δt， 最后依據遞推關系(21)式， 結合邊界和初始條件計算得到溫度場.

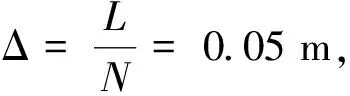
Δt≤49.062 5 s

計算時間取100 min， 則所需時間步為：

m=122.29

取Δt=49.062 5 s時，FO=0.187 5，Bi=5/3， 帶入(21)式， 得：

(23)

至此得到該例的顯式差分格式， 已知初始溫度分布T(x， 0)和邊界條件TA，TB， 依次沿著時間步向下計算， 可得到所有節點任意時刻溫度值. 計算示意圖見圖5， 橫軸為節點位置，i表示第i個節點； 縱軸為時間步，j表示第j個時間步.

圖5 顯式差分示意圖

由圖5可見， 顯示格式遞推關系清晰， 易于計算， 根據(23)式采用MATLAB編程計算溫度場即可.

2.1.2 常系數隱式求解

采用隱式格式求解熱傳導問題時， 根據精度要求， 選取空間網格Δ大小， 隱式格式的差分方程沒有穩定性要求， 時間間隔可根據需求選定. 通過(22)式， 結合邊界和初始條件， 求解方程組， 得到溫度場.

初始時刻， 時間步j=0. 由(22)式得每個節點上的差分方程為：

寫成矩陣形式：

(24)

其中：K1=1/(2FO)+(1+Bi)·2FO；K=2FO·Bi.

同理， 對于下一個時間步， 也可以得到相似的矩陣形式. 由此可見： 對于隱式格式， 雖然方程的計算不受時間間隔的影響， 但是在求解每一時刻各節點溫度值時， 都需要聯立方程組， 這使得求解計算量變大. 隱式格式求解結構圖見圖6.

圖6 隱式差分示意圖

此時基于矩陣(24)求解， 所采用的方法稱為三對角矩陣算法(TDMA). 取時間間隔為20 s， 空間間隔為0.05 m， 采用MATLAB編程求解矩陣， 即可得到溫度場.

2.2 變系數熱傳導方程

實際上， 當溫度較高時， 材料熱工參數會隨著溫度的改變而改變， 即熱傳導系數和比熱為溫度的函數. 在計算考慮材料熱工參數隨著溫度的溫度場時， 本研究采用歐洲規范EC3[2]中鋼材熱傳導系數和比熱容隨溫度變化關系， 由于材料熱工參數為溫度的函數， 熱傳導方程變為非線性方程， 基于熱傳導方程直接求解會十分復雜. 采用能量平衡的方法建立顯式格式的差分方程， 計算時遵循以下流程： 在已知初始溫度場T0時， 依據EC3規范計算得到初始時刻的熱工參數λ0和C0， 再通過λ0和C0依據差分方程計算新的溫度場T1. 即已知前一時刻熱工參數， 可得到下一時刻新的溫度場， 多次計算得任意時刻的溫度場Tn. 依據以上思路和1.2節內容， 建立差分方程.

對于中間節點， 有：

(25)

(26)

對于左側邊界節點， 有：

(27)

取顯式格式：

(28)

同理， 右側邊界節點：

(29)

若仍取Δ=0.05 m. 由于采用顯式差分格式， 需滿足(20)式與(22)式的穩定性要求. 結合(25)式和(26)式可知， 取初始的熱工參數λ0和C0滿足要求， 帶入參數得：

Δt≤21.36 s 取Δt=20 s

可以看出， 方程中溫度的系數都是隨溫度變化的， 即非線性方程， 采用2.1節中直接求解的方法無法得到結果. 根據(28)式-(29)式， 考慮溫度引起的材料性能改變(遵循EC3規范公式)， 使用MATLAB編程即可計算得到溫度場.

3 有限元對比與分析

基于以上內容， 使用ABAQUS分別建立不考慮熱工參數隨溫度變化的有限元模型MODEL0與考慮熱工參數隨溫度變化的有限元模型MODEL1， 相關參數與2.1節、2.2節保持一致. 模型MODEL0與模型MODEL1均采用C3D8T單元， 分別取x=0 m和x=1 m處截面溫度進行對比.

3.1 常系數計算結果驗證

不考慮材料性能隨溫度變化時， 可采用顯式和隱式兩種差分格式計算， 將2.1節計算結果與MODEL0計算結果進行對比， 以驗證計算結果的準確性(圖7和圖8).

由圖7可知， 當不考慮材料熱工參數隨溫度變化時， 采用隱式差分計算結果與ABAQUS有限元模擬結果高度吻合. 在環境溫度采用國際標準升溫曲線(ISO834)時， 在邊界處， 物體內部溫度變化與環境溫度變化形式相同， 均呈對數形式； 在遠離邊界的物體內部， 溫度變化幅度隨著離邊界距離的增大而減小， 且溫度變化呈指數形式. 對比圖8可知， 采用顯式差分計算在x=0 m邊界處與ABAQUS有限元模擬結果幾乎重合； 在距離邊界1 m處， 顯式計算結果和ABAQUS模擬結果隨著時間的增加相差變大， 但總體差距仍然較小(小于0.03 ℃). 產生這一現象的原因在于， 隱式差分計算中采用的TDMA方法計算結果是理論上的精確解， 而顯式差分的精度取決于網格劃分的大小.

圖7 常系數隱式計算結果

圖8 常系數顯式計算結果

3.2 變系數計算結果驗證

當考慮材料性能隨溫度變化時， 采用顯式差分格式計算， 將2.2節計算結果與MODEL1進行對比， 以驗證計算結果的準確性(圖9)所示.

圖9 變系數計算結果

由圖9可見， 當考慮材料熱工參數隨溫度變化時， 使用2.2節中方法計算結果與ABAQUS有限元模擬結果吻合度較高. 在環境溫度采用國際標準升溫曲線， 考慮材料熱工參數隨溫度變化時， 在邊界處物體內部溫度變化與環境溫度變化形式相同， 呈對數形式； 遠離邊界的物體內部， 溫度變化范圍隨著離邊界距離的增大而減小， 溫度變化呈指數形式. 溫度場變化規律與常系數相同. 可以看到， 采用有限差分法計算時， 不論是常系數還是變系數計算結果與相應的有限元模擬結果均存在誤差， 這些誤差主要來源于兩方面： ①采用有限元軟件計算的溫度場實際上是采用有限單元法計算的， 本研究采用的是有限差分法， 不論是有限單元法還是有限差分法， 兩者作為數值方法本身就與精確解存在誤差； ②兩種方法的計算精度不僅與時間網格、空間網格大小的有關， 有限單元法中選取的形函數、有限差分法中省略的高階項也直接影響相應的計算精度.

3.3 常系數、變系數計算結果對比

為探究是否考慮材料熱工參數對溫度場的影響， 分別取離左側邊界x=0 m，x=1 m處截面兩種情況下顯示格式計算所得溫度場進行對比， 并進行誤差分析， 結果見圖10和圖11.

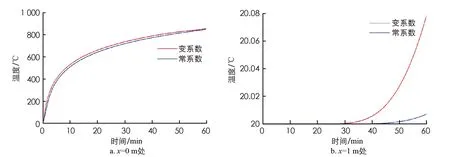
圖10 變系數和常系數溫度場對比

圖11 變系數和常系數溫度場誤差對比

由圖10可見， 是否考慮材料熱工參數隨溫度變化不影響溫度分布規律， 但改變了溫度大小： 考慮材料熱工參數隨溫度變化時的溫度相對于不考慮材料熱工參數隨溫度變化時的溫度偏高. 由圖11可見： 采用有限差分法時不論是否考慮材料熱工參數隨溫度變化， 兩者所產生的誤差具有相同的變化規律， 但不考慮材料熱工參數隨溫度變化產生的誤差總是高于考慮熱工參數隨溫度變化的誤差； 圖11a中， 除時間t=20 s時誤差為60%， 其余各個時間誤差均小于10%， 這是由于采用的升溫曲線初始溫度變化快， 同時計算時所取時間步長較大引起的. 因此， 當環境溫度較高或溫度變化速率較大時， 計算物體溫度場時應考慮材料熱工參數隨溫度的變化， 且取更小的時間空間網格以提高精度.

4 結論

本研究在推導求解變系數熱傳導問題的基礎上， 以具有熱對流邊界條件同時考慮材料熱工參數隨溫度變化的一維瞬態熱傳導問題為例， 采用有限差分法分析了當環境溫度為國際標準升溫曲線時物體內部溫度分布情況， 得到以下五點結論.

1) 基于能量平衡建立傳熱有限差分方程相對于從熱傳導方程出發建立傳熱有限差分方程， 過程清晰、可考慮熱工參數隨溫度變化的情況， 更適用于特殊復雜情況.

2) 通過與相應的有限元模型計算結果對比表明： 本研究采用基于能量平衡建立的有限差分解法能有效計算考慮材料熱工參數隨溫度變化時的溫度場.

3) 是否考慮材料熱工參數隨溫度變化不影響溫度分布規律， 但影響溫度大小： 考慮材料熱工參數隨溫度變化時得到的溫度場， 高于不考慮熱工參數變化得到的溫度場.

4) 在環境溫度采用國際標準升溫曲線(ISO834)時， 在邊界處， 物體內部溫度變化與環境溫度變化形式相同， 均呈對數形式； 在遠離邊界的物體內部， 溫度變化幅度隨著離邊界的距離增大而減小， 且溫度變化呈指數形式.

5) 依據本研究的思路也可計算二維、三維溫度場， 進一步就特定的環境溫度提出相應的物體內部溫度場簡化計算方法.