基于宏觀基本圖的城市路網交通流狀態分析算法應用

姜海巖 ZYRYANOV Vladimir

(頓河國立技術大學道路交通系 頓河畔羅斯托夫 344000)

0 引 言

隨著現代大型城市的迅速發展，城市交通需求的增加,有關交通流特征參數之間相互關系的研究，多為對現有的交通流宏觀模型進行參數結果校正或二次開發，即根據經驗數據和模擬結果確定更準確的宏觀模型參數[1-2].

交通流網絡宏觀模型下一階段的應用與二流交通流理論的提出有關，該理論將交通流與流體力學理論模型相類比，將其分為“動態流”與“靜止流”.“動態流”代表路網中行駛暢通的交通流，“靜止流”代表因交通管控或交通擁堵而暫時停留的交通流，該理論較好地模擬了城市路網交通流的特點，為交通流宏觀模型在城市路網層級的應用奠定了基礎.

Daganzo[3]闡述并定義了一種具有監控和管理網絡功能的宏觀交通流模型——宏觀基本圖(macroscopic fundamental diagram, MFD).MFD描述了城市道路網絡中駛入和駛離網絡的車輛累積與宏觀交通流參數之間的基本關系.經過多個大型城市的路網數據的實際驗證得出結論，即MFD所描述的這種關系在大型城市路網中基本存在，其得到的宏觀交通流參數關系圖像可作為城市路網交通流管理的基本工具[4-8].Ji等[9]使用MFD的基本屬性設計處理了具有邊界調整功能的交通分區算法，并根據實際路網數據測試了其有效性.此后的諸多研究均嘗試使用MFD監測路網車輛累積的相關性，針對多個城市交通路網區域進行邊界控制管理[10-12].結合現代數字建模技術和交通流監測手段，將利用MFD所得到的城市交通狀態預測結果及根據其推出的邊界管理策略納入智能交通系統中作為綜合預測模塊是值得期待的前景發展之一.

本文考慮到多個宏觀交通流參數的復雜聯動，基于MFD的監測與管理城市交通路網的功能，設計了根據實際路網應用場景的交通流狀態分析算法模型，利用該模型得到研究路網的車輛累積及城市路網吸引區變化規律.

1 模型構建

城市路網的交通流分布變化通常相較于擁有固定出入口的高速公路更加復雜.然而當城市路網處于早晚交通高峰或者大型聚集性活動時，其交通加載模式也會出現明顯的目標性流動趨勢，即大量處于不同時空分布的交通流量向目標城市路網區域匯集.為分析其中復雜的交通流變化趨勢，文中基于MFD的雙城區路網交通流狀態分析算法[13-14]，并根據頓河畔羅斯托夫市長度為39 km的中心城區路網的實例數據構建其算法分析模型，得出交通流趨勢變化結果.

引入一種新的交通流變量參數“旅行效率(travel production，TP)”為MFD的基本元素之一.TP為

(1)

式中：TP為旅行效率；A為路網中的車輛累積；Aj為路網中的最大車輛累積；vj為阻塞速度；vf為自由流速度；n為修正參數.

在旅行效率與路網累計車輛之間的關系圖像中(見圖1a))可知：研究路網區域在大約為2 500輛的累積水平上實現了最大性能，累積水平為2 000～3 500輛的范圍內有10%的參數最大偏差.這也表明使用TP作為基本元素的圖像形狀對應于使用傳統經典參數“駛離路網的車輛總數”的MFD.在網絡平均速度與路網累計車輛之間的關系圖像中(見圖1b))，大致可將其分為四類網絡運行狀態：A狀態—穩定狀態，平均速度不低于25 km/h；B狀態—網絡性能達到最大值，但平均速度下降到17 km/h；C狀態—擁堵狀態，平均速度急劇下降到7 km/h；D狀態—網絡“閉鎖”狀態，整個網絡因為強烈的擁堵而幾乎無法移動.

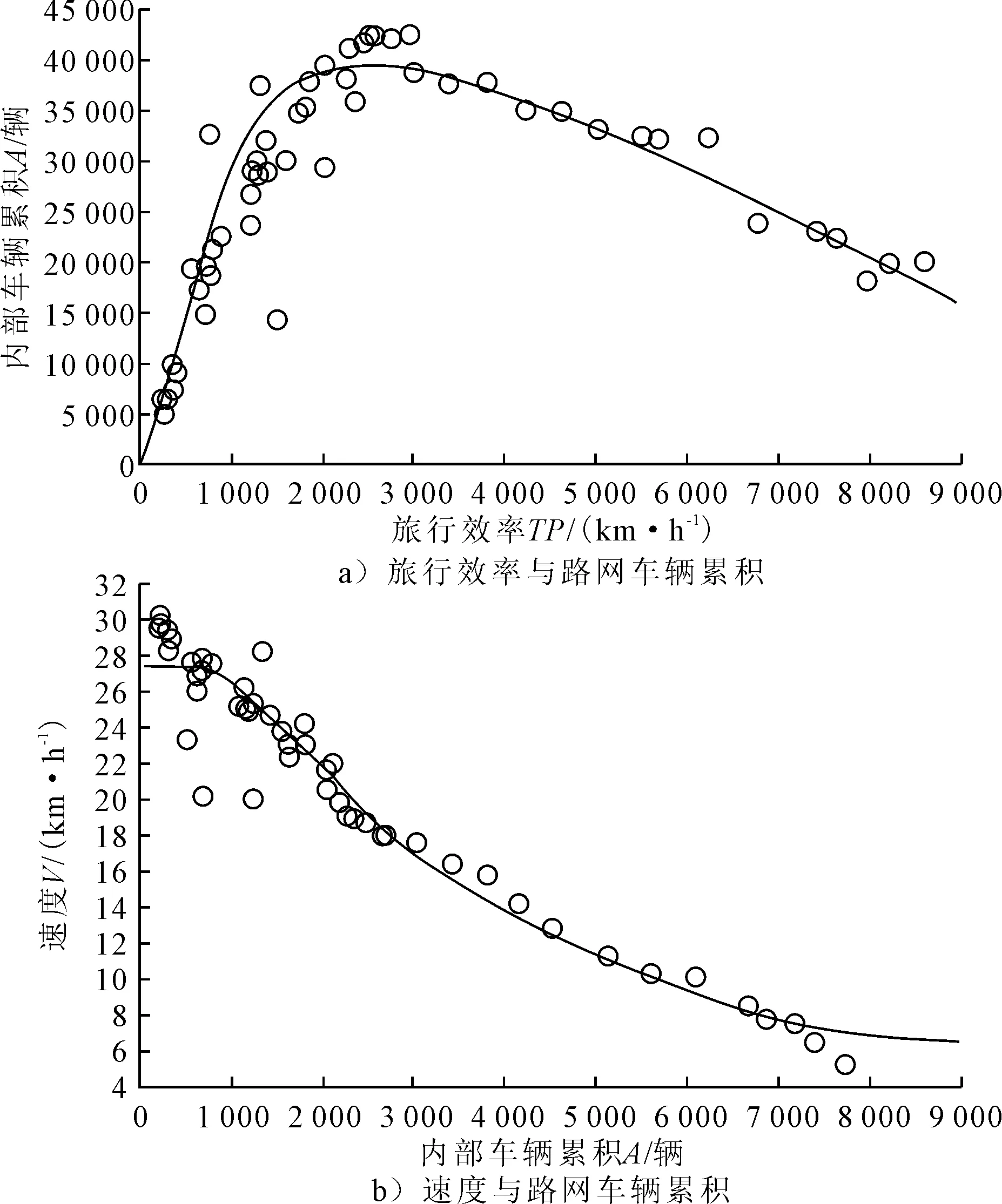
圖1 研究路網MFD

經過大量的交通調查與數據分析，獲取的實例路網中的交通流量趨勢大致可看作主要流量從“外圍區域”向“中心區域”的轉移，而“中心區域”也是通常處于邊界交通控制下的“保護區域”.其中，轉移流量(主要流量)命名為q3，“保護區域”內部流量為q1(內部流量是指起訖點均位于該區域的流量)，而“外圍區域”也存在內部流量為q2.實例路網及其兩城區的流量分布示意圖見圖2.

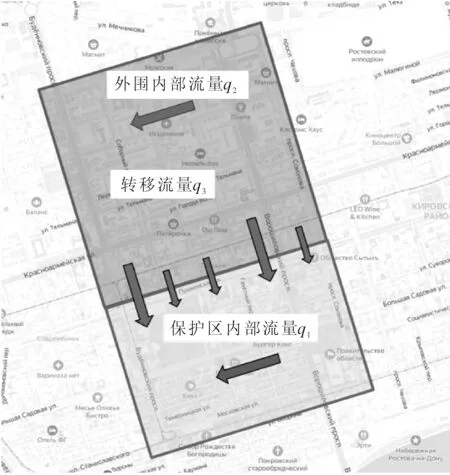
圖2 實例路網及其兩區流量分布示意圖

兩城區交通流狀態分析算法模型框架被描述為

(2)

(3)

TP2(n2(t))·u(t)-TP1(n1(t))

(4)

式中：n1、n2、n3分別為保護區域、外圍區域、轉移流量的車輛累積；q1、q2、q3分別為保護區域內部流量、外圍區域內部流量、轉移流量；TP1、TP2分別為保護區域、外圍區域的旅行效率；u為施加在保護區域與外圍區域之間的邊界控制(其值介于0～1：當u=0時，完全允許流量自由通行；當u=1時，則完全禁止外圍區域流量進入保護區域.)；t為交通流監控時間.

基于上述交通流狀態分析算法的框架公式，構建的模型示意簡圖見圖3.

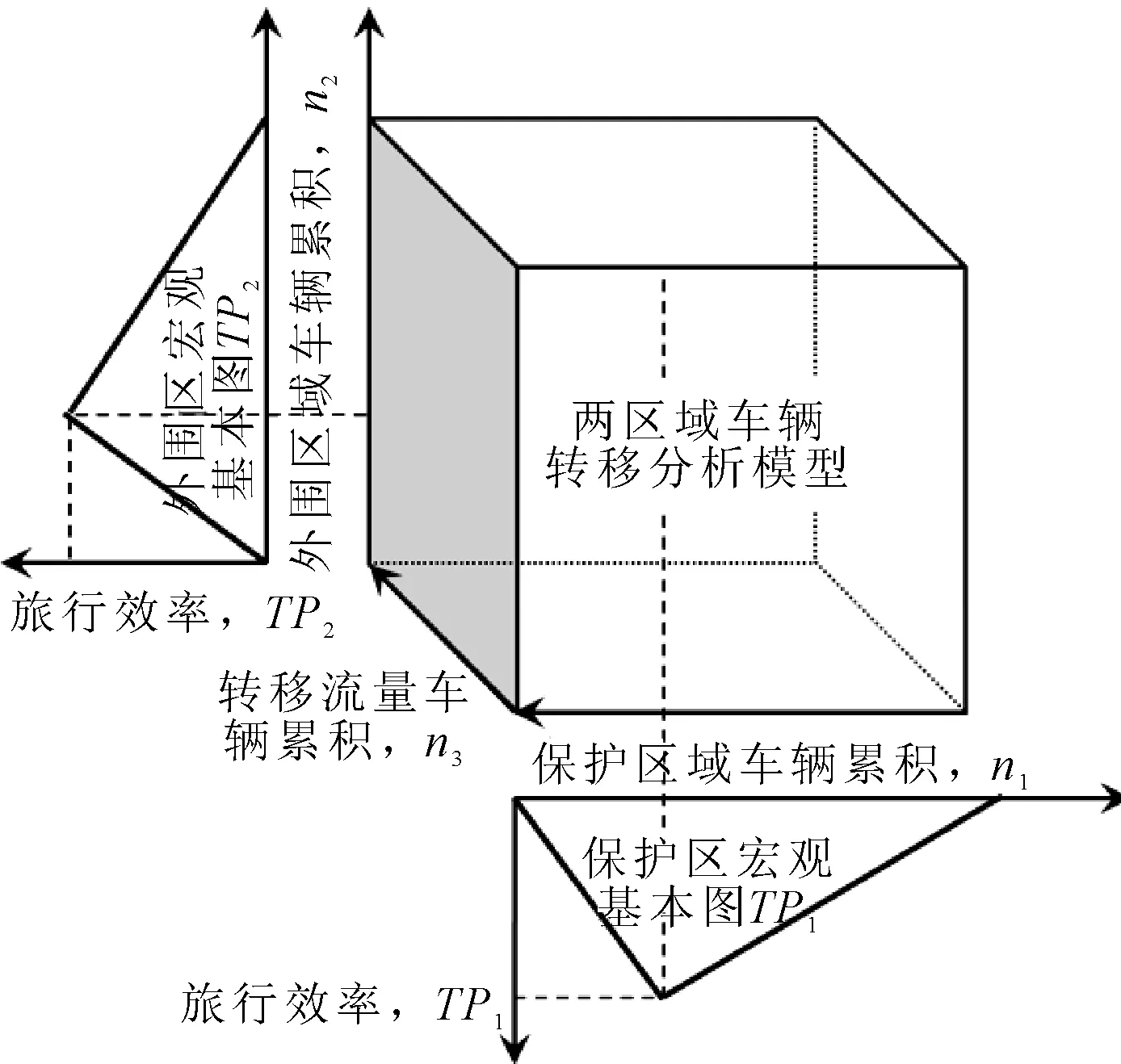
圖3 兩區域交通流分析算法模型示意簡圖

2 車輛累積變化趨勢模擬

通過分析城市路網處于早晚交通高峰或者大型聚集性活動時的交通流量變化趨勢，不難發現在某些情況下向目標城市路網區域匯集的交通流量往往占據絕對的數量優勢，使得外圍區域的內部流量可以被暫時忽略處理.因此，本文在處理兩城區交通流狀態分析建模時，首先考慮基于主要交通流量(即轉移流量q3)對于兩城區車輛累積變化趨勢的影響.

轉移流量q3對于保護區域累積變化趨勢影響的交通流狀態分析算法模型被簡化為

(5)

(6)

以式(5)～(6)的交通流狀態分析算法模型為基礎，通過使用數學建模軟件Matlab進行模擬轉移流量對于兩城區的車輛累積變化趨勢.

圖4為邊界控制分別為u=0.4和0.7的情況下，兩城區車輛累積的相關趨勢變化曲線.所有相關趨勢變化曲線的起點為在兩城區最大車輛累積限制下的任意點.通過分析車輛累積的趨勢變化曲線發現，在某特定區域內的曲線隨著時間的推移最終會達到代表駛離路網車輛數和駛入路網車輛數相等的平衡點，即曲線隨著時間的增加會使式(5)～(6)計算結果趨向于0.這說明，如果兩城區的車輛累積坐標恰好處在這個特定區域內，那么交通路網及其管理系統有能力使駛離路網車輛數和駛入路網車輛數趨于平衡，從而避免發生擁塞現象，此特殊區域命名為吸引區.

圖4中實線圍成的為吸引區，u=0.4時，吸引區落在X軸(保護區域)的邊界坐標為(4 060，0)，落在Y軸(外圍區域)的邊界坐標為(0，3 798)；u=0.7時，吸引區落在X軸(保護區域)的邊界坐標為(3 938，0)，落在Y軸(外圍區域)的邊界坐標為(0，4 946).

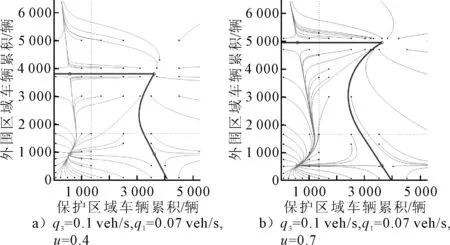
圖4 轉移流量q3對于兩區域車輛累積的影響及吸引區變化

在整理趨向于平衡點的車輛累積變化曲線并繪制吸引區邊界的過程中，在邊界管理u=0.7的情況下，吸引區的面積對比于在邊界管理u=0.4的情況下有明顯的增加，尤其是對于外圍區域的車輛累積有更大的寬容.這說明當實施更加嚴格的邊界控制管理時，交通路網系統對于兩城區車輛累積的處理能力有了明顯的提升，即路網系統允許更大容量的來自外圍區域的轉移流量進入保護區域內，并且路網系統不至于達到不可挽回的擁塞狀態.

為了進一步了解研究兩城區路網的車輛累積曲線及其吸引區的變化性質，在圖5中的模擬圖像中引入了更大的轉移流量和更加激進的邊界控制管理，其輸入數據見表1(轉移流量q3增加到0.3 veh/s，邊界控制管理分別為0.7和0.9).其中u=0.7時，吸引區落在X軸(保護區域)的邊界坐標為(2 842，0)，落在Y軸(外圍區域)的邊界坐標為(0，1 884)；u=0.9時，吸引區落在X軸(保護區域)的邊界坐標為(2 690，0)，落在Y軸(外圍區域)的邊界坐標為(0，2 659).

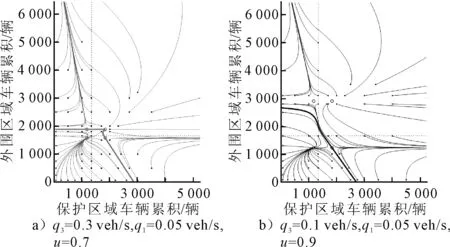
圖5 轉移流量q3增大對于兩區域車輛累積的影響及吸引區變化

通過模擬數值實驗發現，對于轉移流量的增大，導致交通路網系統的吸引區面積明顯減小，即路網系統對于逐漸增大的轉移流量的處理能力越來越弱.雖然施加更為激進的邊界控制管理u=0.9改進了路網系統對于轉移流量的處理能力，但是其吸引區形狀與算法卻完全不同與圖4和圖5a)的結構.

因此根據圖4和圖5得到的模擬結果.在圖6的模擬中引入了更廣的邊界控制管理數值范圍，以此得到吸引區在不同邊界控制管理下的變化規律.在邊界控制管理數值不斷增大的過程中，吸引區的范圍也在不斷增大，這說明有效率的邊界控制使得交通路網系統有能力處理和接納不斷增加的來自外圍區域的車輛累積.然而來自外圍區域的車輛累積擠壓了對于保護區域自身的內部流量累積，使得在吸引區在保護區域車輛累積上的坐標數值越來越小.需要注意的是由于圖6b)引入的轉移流量較大，因此u=0.7～0.9幾乎就是其可以施加的最小和最大邊界控制管理的范圍，這也可以說明轉移流量越大，可施加的邊界控制管理u的范圍越小.

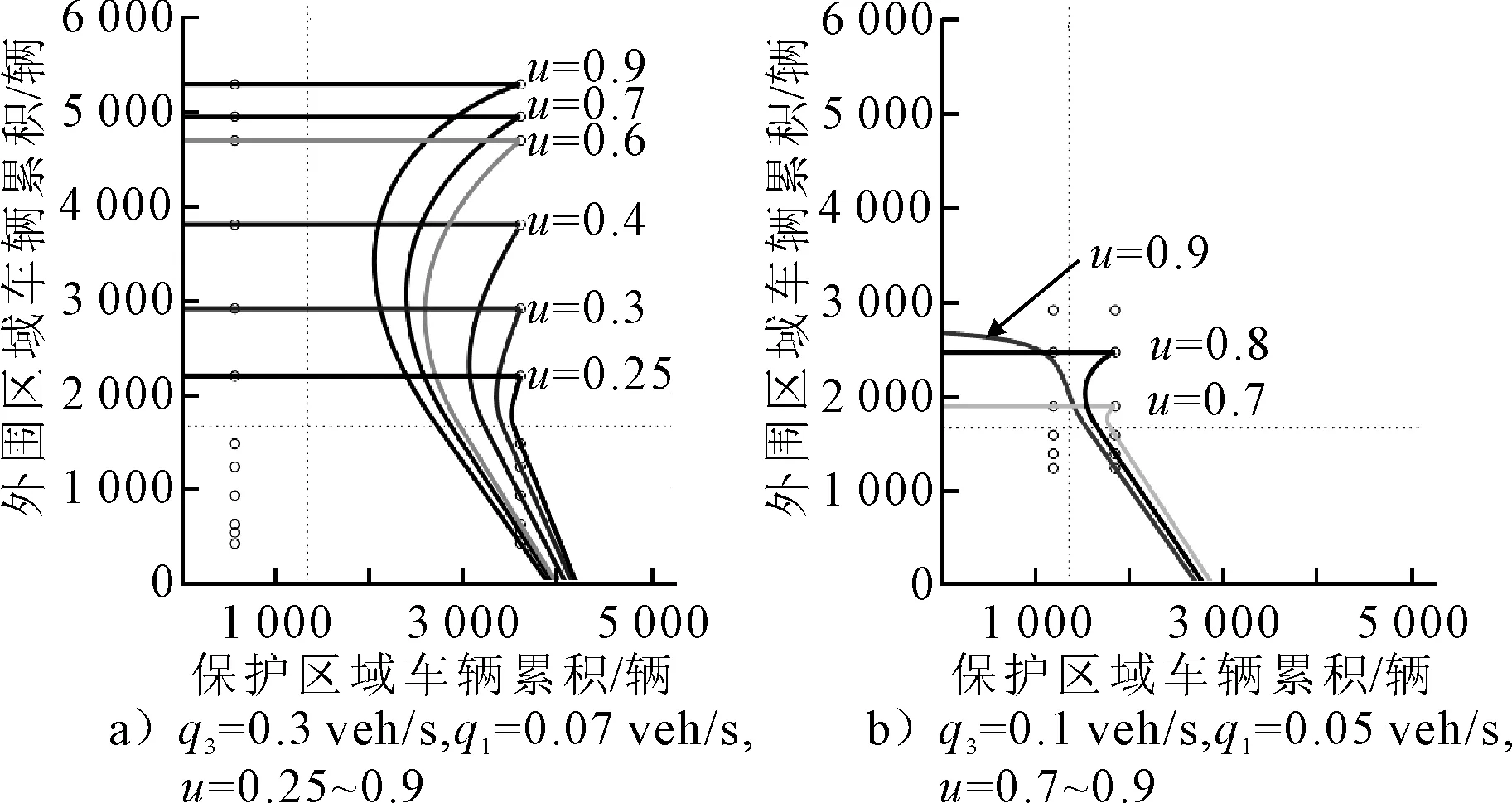
圖6 在不同轉移流量q3下邊界控制u對于吸引區變化的影響

3 區域內部流量和轉移流量對交通流狀態的影響

分析主要由轉移流量對城市路網區域交通流狀態帶來的影響時，尚可以在二維平面坐標系描述其車輛累積和吸引區面積的變化趨勢.當考慮區域內部流量時，就需要引入更加復雜的三維分析算法結合數值實驗模擬來解決此類問題.

轉移流量q3所產生的轉移車輛累積n3也是整個外圍區域所產生的車輛累積的一部分，即外圍區域內部流量q2所產生的車輛累積n2與轉移車輛累積n3一起構成并推導出了外圍區域MFD的旅行效率.

為了使交通流狀態分析算法模型更具有一般性，圖7為在邊界控制管理u的數值上取中間值u=0.4，轉移流量為0.1 veh/s和保護區域內部流量為0.07 veh/s的兩城區吸引區變化規律.對于模擬結果得到的吸引區，其外圍區域車輛累積n2采用的數值實驗模擬輸入數據分別為(從下至上)n2=0 ，500，1 000，1 500，2 300 veh.隨著外圍區域的內部車輛累積n2的取值逐漸增大到500 veh時，吸引區的面積卻比只考慮轉移流量對其帶來的吸引區還要更大，這是由于內部流量產生的車輛累積占據了一部分外圍區域的車輛累積，從而導致了轉移流量的相對比例減小.圖8為圖7的俯視圖，更直觀的表達出用實線繪制的吸引區Ab1比當n2=0 veh時繪制的吸引區面積更大.然而當增加轉移車輛累積n3占整體外圍區域所產生的車輛累積(n2+n3)的比例時，其產生的吸引區Ab2比實線繪制的吸引區Ab1面積要大.這是由于該比例改變了轉移臨界車輛累積、轉移旅行效率等參數，從而改變了轉移流量的MFD所導致的結果(Ab1的比例因子為7/8，Ab2為11/12).此外，在考慮區域內部流量和轉移流量的三維坐標系中，其車輛累積變化趨勢曲線(見圖7～8的累積走勢曲線)仍然遵循二維坐標系中的變化規律.

外圍區域的內部車輛累積n2的取值逐漸增大到1 000 veh時，吸引區的面積開始比只考慮轉移流量對其帶來的吸引區更小，這是由于內部流量產生的車輛累積隨著時間的推移造成了外圍區域加速擁擠，導致擁堵外溢對保護區域造成了影響所致.同理可以觀察到，隨著外圍區域的內部車輛累積n2的進一步加大(n2為1 500，2 300 veh)，所對應的吸引區越來越小.然而與Ab1和Ab2相同的原因，不同的轉移車輛累積n3占整體外圍區域所產生的車輛累積(n2+n3)的比例，也造成了吸引區Am1和Am2的不同.

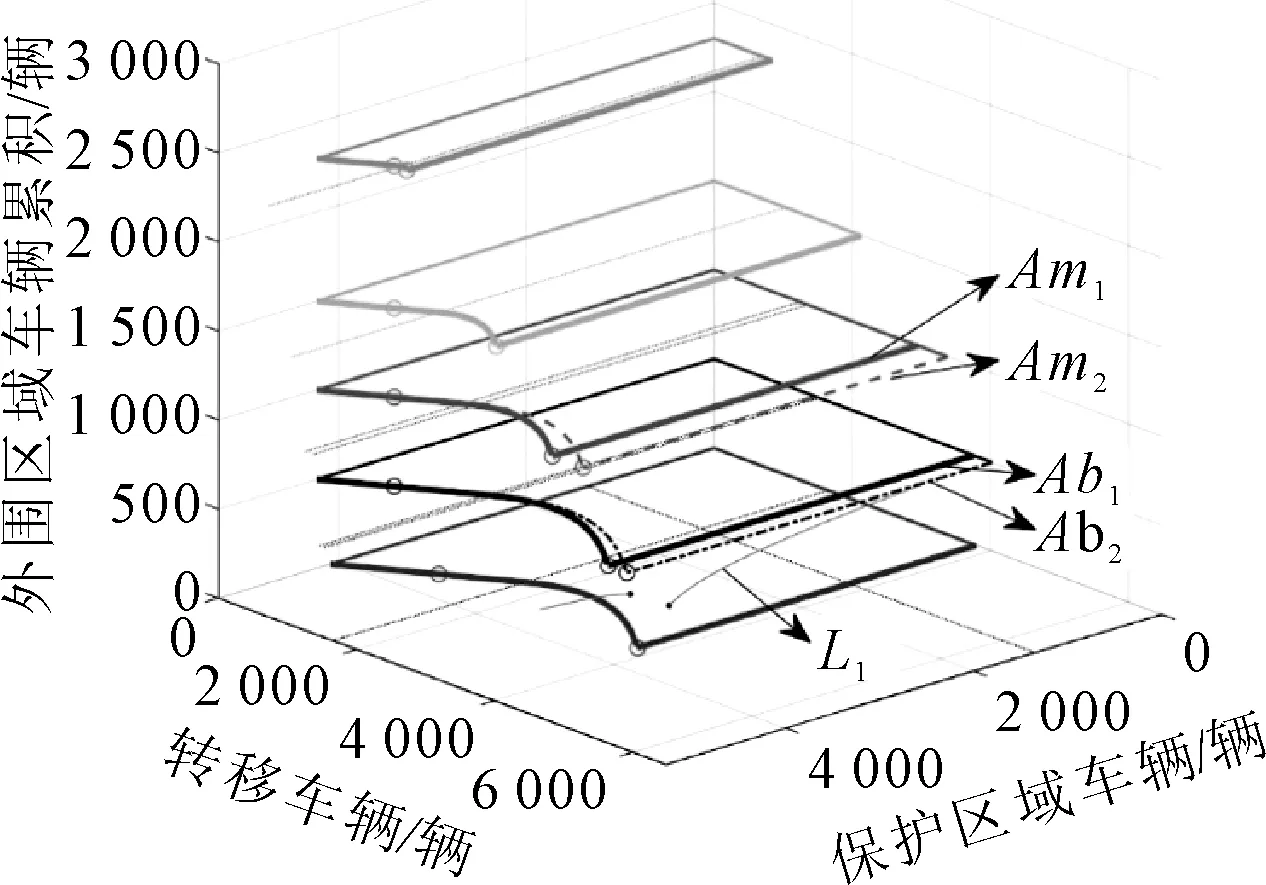
圖7 考慮不同外圍內部流量q1的吸引區變化規律(q3=0.1 veh/s，q1=0.07 veh/s，u=0.4)

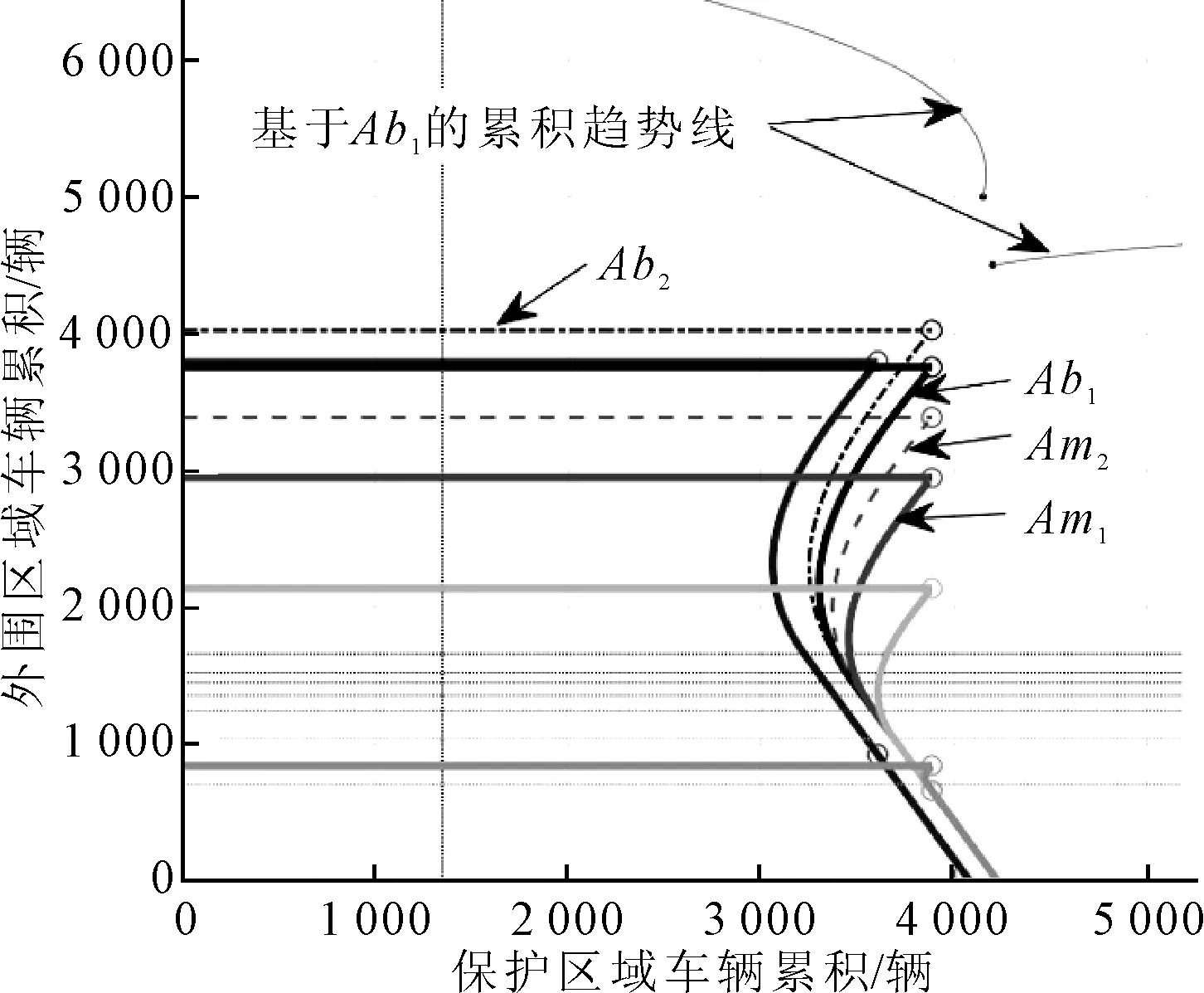
圖8 吸引區變化規律圖7的俯視圖

4 結 束 語

本文引用了新的MFD參數“旅行效率”，結合頓河畔羅斯托夫長度為39 km的實際路網數據構建了兩城區城市路網交通流狀態分析算法模型.在此算法模型基礎之上，通過數學模擬得到了在二維坐標系內表示的主要由轉移流量對于兩城區車輛累積的影響及其交通流吸引區變化趨勢.為了擴大分析算法的適用性，進一步考慮內部流量對路網系統的影響，提出了在三維坐標系內表示的兩城區車輛累積的交通流吸引區變化趨勢.

本文驗證了參數“旅行效率”在參與交通流狀態分析時與MFD經典參數效用相同，揭示了兩城區內部流量和轉移流量以及邊界控制管理對于兩城區城市路網車輛累積變化的關系.說明了在兩城區交通流管理優化過程中，管理區域內部流量及其產生的車輛累積與合理調節邊界控制一樣重要，為接下來精準的交通流管理奠定了理論分析基礎.

下一步的研究重心是結合該多變量三維坐標交通流狀態分析方法進行多范圍的邊界控制管理數值模擬，進而提升制定針對雙城區城市路網交通流狀態的動態邊界管控策略的能力.