多風向角側風下動車組明線運行的氣動特性

王東屏, 趙潔,羅煥,劉超

(1.大連交通大學 機械工程學院,遼寧 大連 116028;2.大連交通大學 機車車輛工程學院,遼寧 大連 116028)①

列車速度的提高使得列車與空氣的相互作用變得更加強烈[1].在實際的車輛運行過程中，隨著側風風向角的增大，列車空氣動力性能逐漸惡化，列車各項氣動力迅速增大，影響了列車的橫向穩定性[2].傾覆力矩的增大導致列車失穩而脫軌和傾覆[3]，行車的阻力增大，使得運營能耗增大，同時對列車高速運行的安全性、穩定性也帶來重大影響[4].因此，為了使列車安全通過風區，必須開展側風環境下的列車空氣動力特性研究.

目前，許多學者都對高速列車側風下運行進行了大量研究，李西安等[5]研究了在列車明線運行時，不同網格劃分對計算結果的影響，并與風洞試驗數據進行比較.同時研究了橫風作用下、不同車速和風速下列車的氣動性能變化規律.郗艷紅等[6]研究了單列高速列車在明線橫風環境中運行時的氣動特性，將來流速度為60 m/s，風向角為3°和6°時列車模型氣動力系數與風洞試驗的數據進行對比，得出了橫風風速和風向角及車速對列車氣動特性的影響規律.高廣軍[7]研究了在強側風作用時，車—路耦合條件下車輛的氣動性能，在風向角為90°時，車輛受到的氣動力最大，并且氣動力隨著車速和風速的增大而增大.

雖然上述文章對高速列車側風明線運行的氣動特性進行了大量的計算分析，但多為改變車速和風速來對列車氣動特性進行分析，對于變角度的研究較少，且與試驗數據的對比驗證較少，所以仍然需要對多個風向角下列車的空氣流場進行數值分析.

本文應用Fluent流體分析軟件，在多風向角側風環境下，對動車組三車編組的空氣動力流場進行數值仿真，將表面測點的壓力系數結果與風洞試驗結果進行對比，研究不同風向角下列車的表面壓力系數規律、流場速度及各項氣動參數，為動車組側風環境下安全運行指標的確定提供技術支持.

1 計算模型

1.1 幾何模型

列車計算模型取三車編組，即：動力車+拖車+動力車，車輛之間以風擋連接.對列車某些局部結構進行簡化處理，最大限度地呈現列車外形原貌.動車組整車計算模型見圖1.

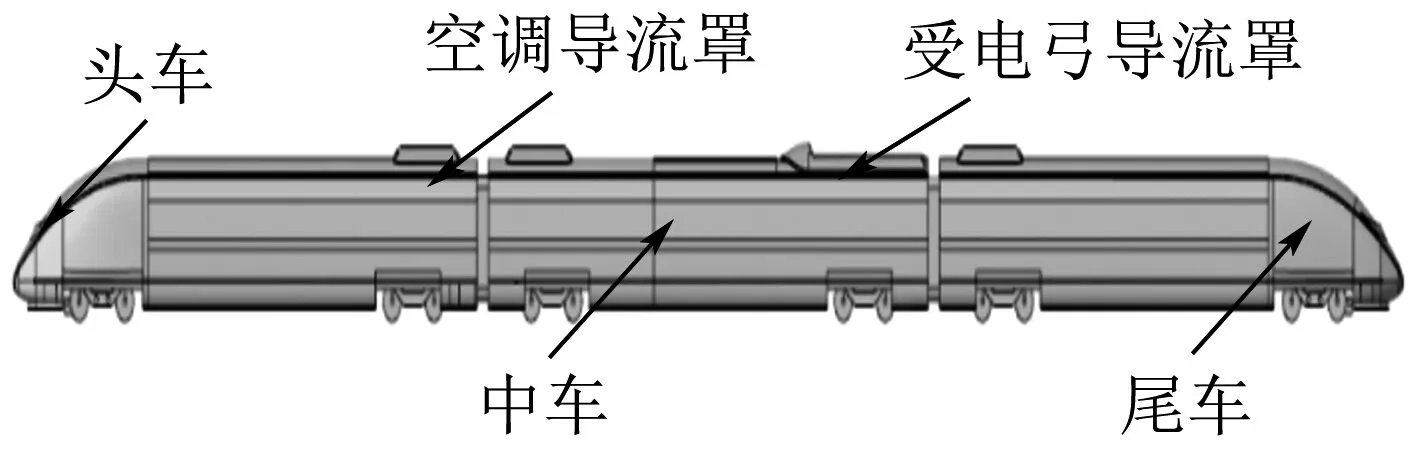
圖1 動車組整車計算模型

為避免列車在尾部產生繞流，從而影響計算精度，設列車前端流場區域的縱向長度為25倍的列車高度，列車尾流區域的縱向長度至少大于2倍的列車總長度，計算域高度約為20倍的列車高度[8].考慮到側風問題，擴大流域兩側面的區域，設側方流場區域為2倍的列車總長度，最終確定整個計算區域為368 m×280 m×90 m.

1.2 網格劃分

列車表面采用三角形網格劃分，四周的矩形區域內部均采用幾何適應性強的四面體非結構化網格，按照距離壁面的遠近在車體周圍劃分三層區域：流域一、流域二和流域三，且網格大小依次減小.網格總數約為1 400萬，整體流域的網格劃分見圖2.

圖2 整體流域的網格劃分

根據列車結構的不同，對其進行不同程度的網格劃分， 研究車身特殊部位時需要對網格進一步加密，如列車頭部、 空調導流罩、 受電弓導流罩及與車身連接處的細小結構，車頭剖面網格劃分見圖3.

圖3 車頭剖面網格劃分

1.3 計算方法

運用有限體積法對高速列車三維外流場進行數值模擬.列車周圍流場為不可壓縮、定常、黏性流體流動，故采用RANS方法[9]和RNGκ-ε雙方程湍流模型對其空氣流場進行仿真計算.計算方法使用SIMPLE來耦合壓力—速度流場，對流項使用二階迎風格式進行離散，黏性項為中心差分格式.

2 計算條件

2.1 邊界條件

本文模擬列車在風洞中吹風試驗的方式，給定邊界條件，風速采用合成風[10].入口和迎風面設定為速度入口，風速為60 m/s；出口和背風面設定為壓力出口，靜壓為0.根據列車與周圍空氣的相對運動，列車整體設置為無滑移壁面，地面設置為滑移壁面，滑移壁面的速度與車速大小相等、方向相反，以體現其與列車之間的相對運動.

側風是風向與列車運行方向呈一定角度的環境風[10].列車側風風向角示意圖見圖4，假定風向角為0°時以速度v吹向列車，設定方向為西北角度的側風角度為負，西南方向的側風角度為正.對風速為60 m/s、側風風向角為-24°～+24°(間隔為3°)的17個計算工況進行了數值模擬.邊界條件定義見表1.

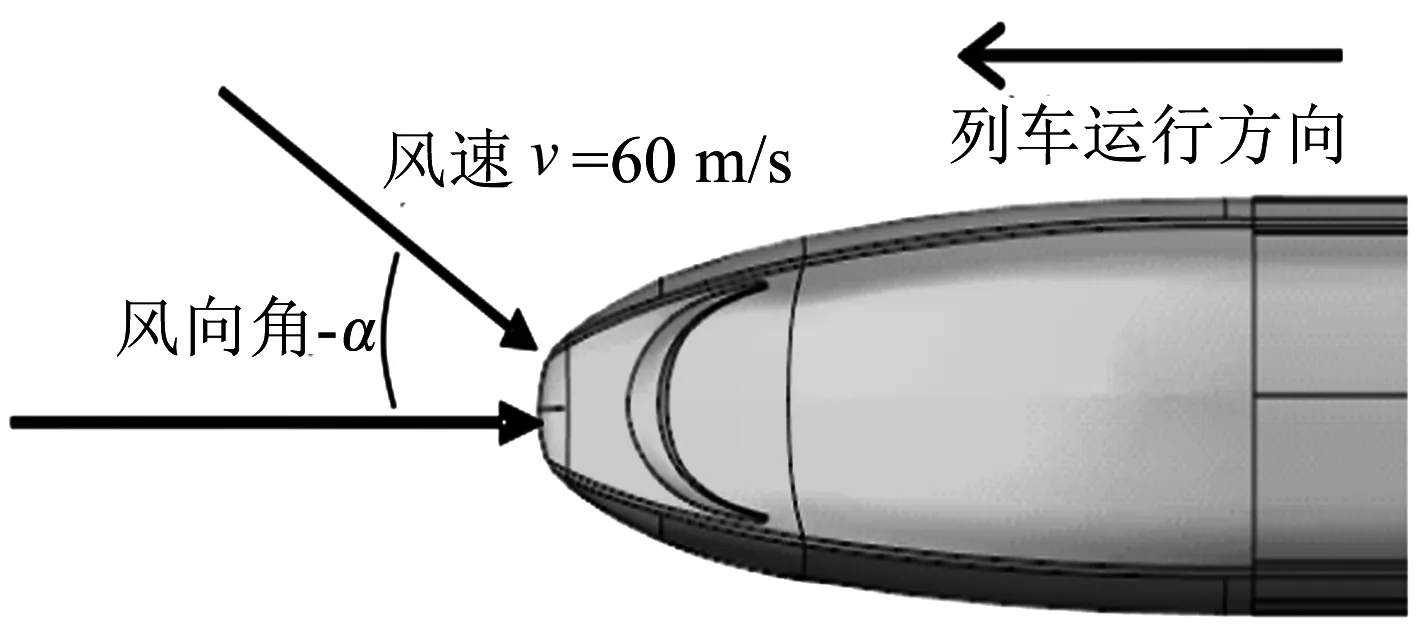
圖4 列車側風風向角示意圖

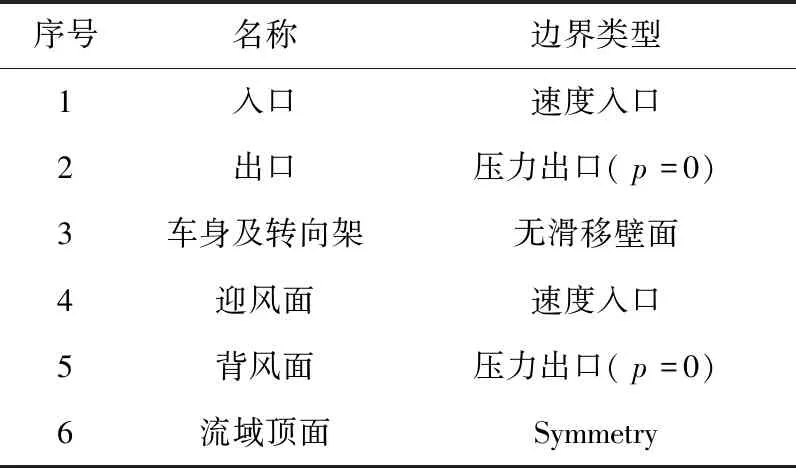
表1 邊界條件定義

2.2 車身表面測點的建立

在風洞實驗室中對動車組1/8 原型車進行了吹風試驗[11].為了獲得列車的表面壓力系數，風洞試驗中在列車車頭和空調導流罩表面共計布置了若干個測壓點，數值模擬中為保證建立模型測點的準確性和方便性，降低與風洞試驗中列車車身測點表面壓力系數對比的誤差，因此在建立模型時設置與風洞試驗相同位置的測點，測點通過在車身表面選取面單元方式創建.

3 結果分析

3.1 測點壓力曲線結果對比

按照風洞試驗報告內容選取的測點位置分別為頭車鼻端前緣處和空調導流罩上表面中點處，將數值模擬得到相應的表面壓力系數與風洞試驗數據進行對比，圖5為兩個測點壓力系數隨風向角變化的曲線對比，風洞試驗數據來源于參考文獻[11].

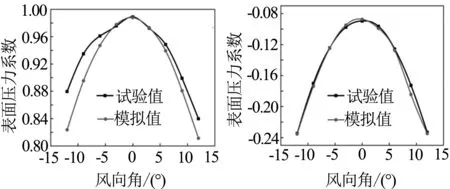
(a) 鼻端前緣處 (b) 空調導流罩上表面中點處

圖5表明車身測點表面壓力系數的數值計算結果與風洞試驗的壓力系數曲線變化趨勢一致，但數值計算略小于風洞試驗值.其表面壓力對比的具體誤差見表2.

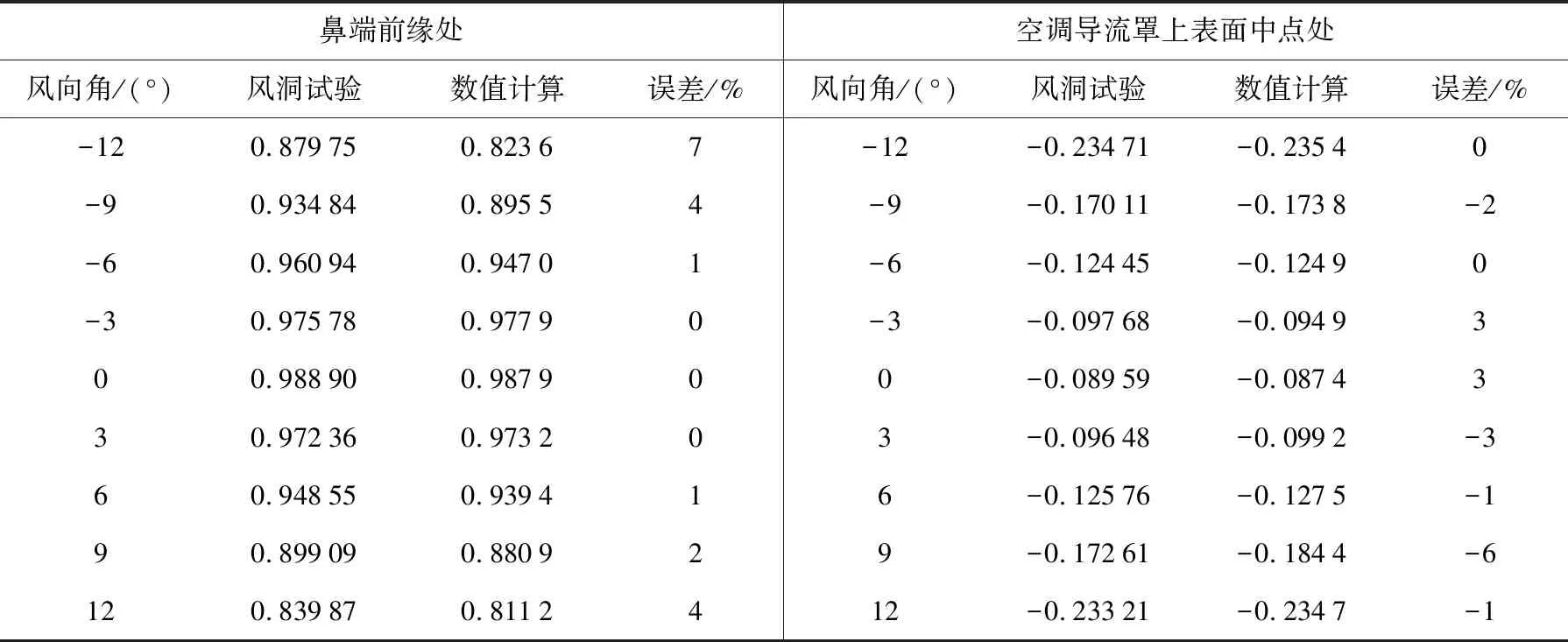
表2 風洞試驗與數值計算表面壓力系數的比較

由表2可知，數值模擬與風洞試驗的測點表面壓力系數誤差為10%左右，存在誤差的原因主要有:數值模擬的幾何模型與列車模型之間存在幾何誤差；數值模擬的送風方式為均勻風，而風洞試驗的風場設定未完全按照均勻風送風；數值模擬的計算環境與風洞試驗的試驗環境無法保持完全一致.

可見，風洞試驗與數值模擬結果之間存在合理誤差，這驗證了測點建立的準確性及模型計算方法的可行性，說明數值計算結果具有一定的參考價值.

3.2 側風工況計算結果分析

3.2.1 車體表面壓力分布

當列車在側風環境中運行時，列車空氣動力性能進一步惡化.表面壓力分布規律不同于明線運行時的壓力分布規律，不同風向角下車體表面壓力云圖見圖6.

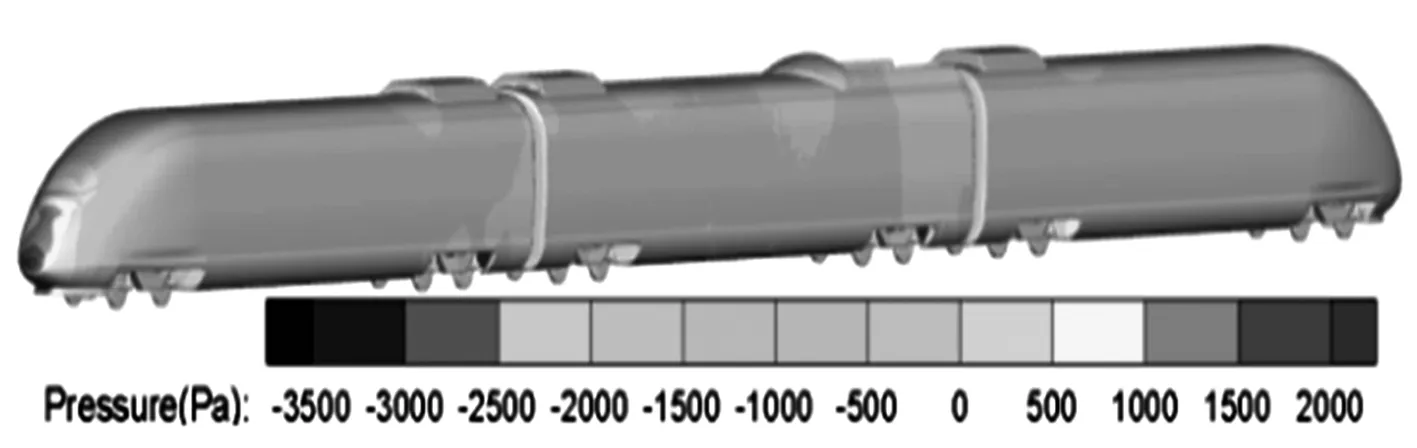
(a) 0°迎風側列車表面壓力云圖

(c) -9°迎風側列車表面壓力云圖

從圖中可知，無側風時列車車體表面壓力分布的變化范圍較小，迎風側和背風側負壓范圍較多，表面壓力最大值位于頭車鼻尖前緣點，此時車身表面最大壓力為2 199 Pa，最小壓力為-3 813 Pa.當風向角增大到-9°時，列車迎風側大部分為正壓區，背風側均為負壓區，頭部的壓力滯止點偏離列車前緣鼻端處，出現在車頭鼻尖迎風側處,此時最大壓力為2 300 Pa，最小壓力為-5 169 Pa，較無風時最小壓力減小了36%.風向角進一步增大到-24°時，列車迎風面處于較大正壓狀態，由于兩側面的壓差較大，有大量的漩渦產生和脫落，使得背風面處于高負壓狀態.空調導流罩和受電弓導流罩與車體相接處均呈現較大的正壓，在拐角處產生較高負壓，由此造成列車前后壓差使列車承受的阻力增大；隨著風向角的增大，空調導流罩和受電弓導流罩所受到的側向力也逐步增大.

3.2.2 風向角為-24°時的速度矢量分布

列車頭部在距地面1.8 m的水平橫斷面上的速度矢量分布見圖7，列車尾部橫剖面外輪廓周圍速度矢量分布見圖8.

圖7表明，由于風向角的增大，造成列車表面壓力、速度分布的不對稱性.當氣流經過鼻端繼續沿車體流動時，車身表面的壓力開始下降，表面壓力最大處為迎風側速度來流處.

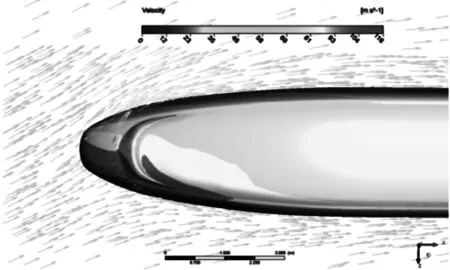
圖7 列車頭部周圍速度矢量分布

圖8表明，列車在側風環境下運行時，在列車背風側，空氣流動產生旋渦，故背風側空氣速度明顯小于迎風側速度.列車周圍最大速度為114.11 m/s.由于轉向架與車體之間空間較小，導致氣流流動空間變小，氣流方向發生改變，其中一部分氣流進入車身下方轉向架區域內，由于此處車體端墻區域周圍相對封閉，導致轉向架周圍的氣流無法及時導出，因此在轉向架周圍氣流速度較小.

圖8 列車尾部橫剖面外輪廓周圍速度矢量分布

3.2.3 風向角對氣動性能的影響

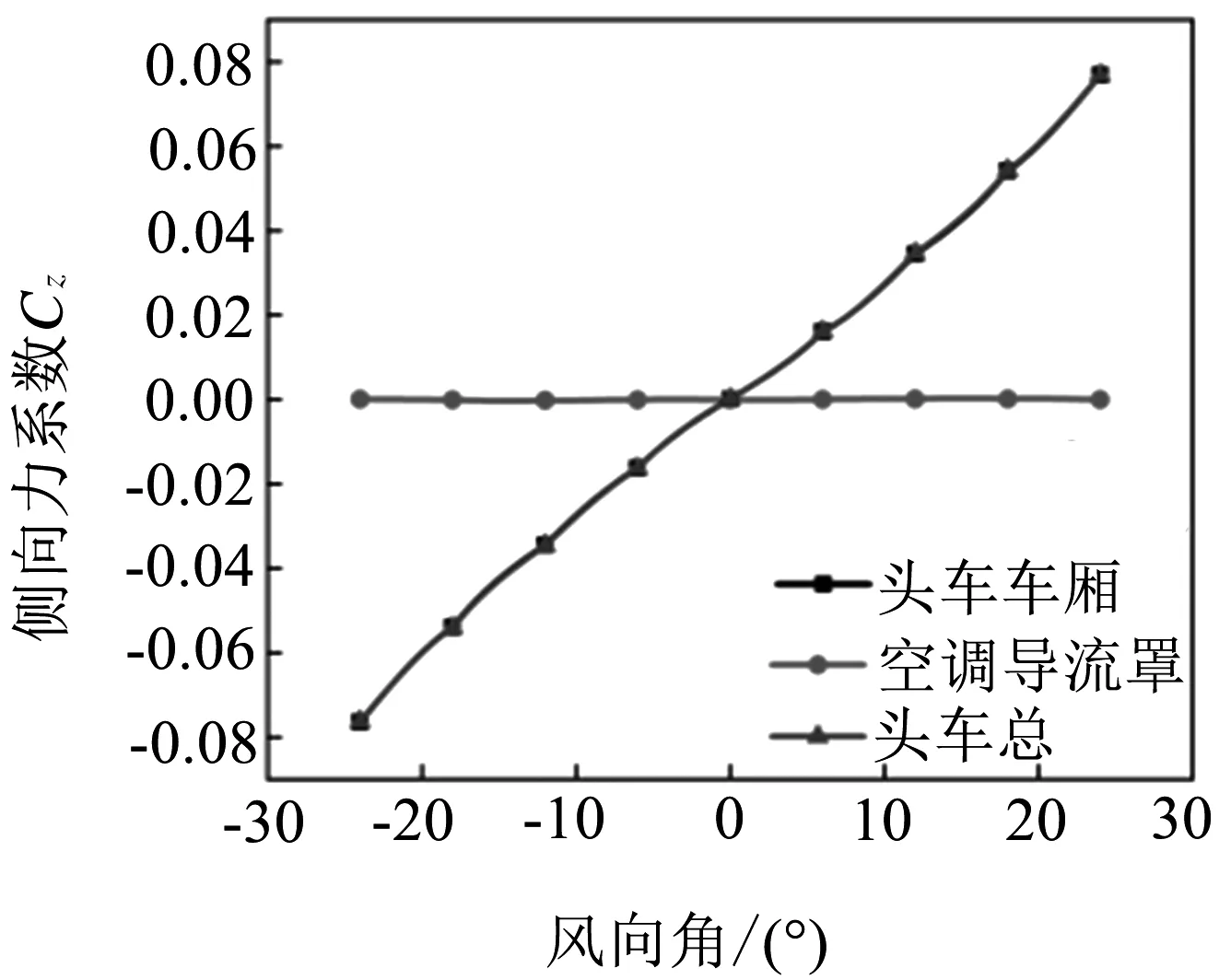
高速列車在側風環境中運行時，隨著側風風向角的變化，列車承受的阻力、側向力均在不斷變化.動車組在側風環境中運行時，風速設定為60 m/s，列車各部分阻力系數和側向力系數隨風向角變化曲線見圖9、圖10.

圖9(a)表明，隨風向角的增大，頭車所受阻力系數先增大后減小，這是由于車頭形狀為曲面，風向角為0°時，來流速度垂直于車頭，有風向角時，來流速度并非完全垂直于車頭，車頭曲面處受到的力被分解為垂直來流速度方向的切向力和垂直車頭曲面切線的力.隨角度的增大，阻力逐漸增大，當角度增大到10°時，頭車阻力系數達到最大，此時空調導流罩所受阻力占總頭車阻力的3%，隨著角度進一步增大，阻力逐漸減小.圖9(b)表明，在-24°～24°范圍內，中車的阻力系數隨風向角增大逐漸增大，空調導流罩阻力系數曲線呈現先增大后減小的趨勢，其阻力在無風環境下占據總的中車的4%，受電弓導流罩阻力系數曲線在此范圍內呈現先減小后增大的趨勢，在24°時占據總的中車阻力的14%，可看出在列車運行過程中，受電弓導流罩對列車中車所受阻力的影響較大.圖9(c)表明，尾車的阻力系數曲線變化趨勢與中車的變化趨勢相同， 空調導流罩阻 力 系數曲線在-24°～24°范圍內基本也成呈現先增大后減小的趨勢，當阻力系數達到最大時，所受阻力占總的尾車阻力的2%.圖9(d)表明，中車所受阻力最大，且由圖9(b)可看出因受電弓導流罩的存在，導致中車承受的阻力較大，其阻力系數比風向角為0°時增大了97%，頭車的阻力系數變化范圍明顯小于尾車，整車的阻力系數在方向角為12°時增大了68%，24°時增大了103%.

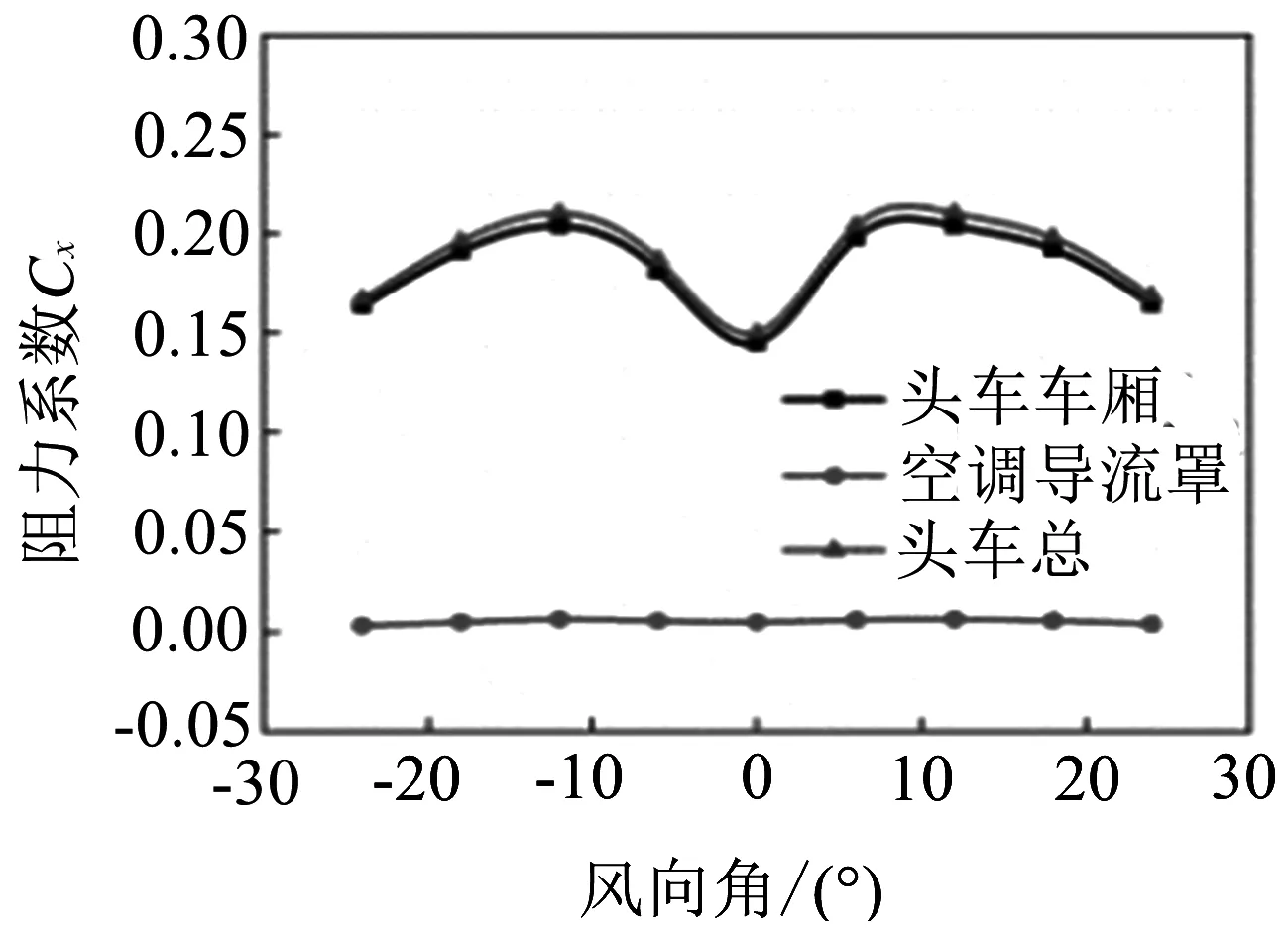
(a) 頭車

(a) 頭車

根據數據分析，對側風風向角與列車氣動阻力系數進行高斯曲線擬合，整車阻力系數的擬合曲線相關系數范圍為0.974 29～0.983 93，高斯曲線表達式為：

Cx=C0+Ae(-0.5((x-xc)/w)2)

(1)

式中:C0=0.862 76；A=-0.408 54；xc=0.115 14；w=8.338 69;e取2.718 28.可計算出列車在不同風向角下的氣動阻力系數.

圖10(a)、10(b)表明，在0°～±24°范圍內，頭車和中車側向力系數絕對值均隨風向角的增大而逐步增大，受電弓導流罩所受側向力的絕對值隨風向角增大而增大；風向角從0°變化為24°時，側向力系數從6.24×10-5變化為0.001 6，增大了24倍；當風向角到達24°時其側向力系數占總中車的4%，車頂空調導流罩受到的側向力占總側向力的3%.圖10(c)表明，尾車的側向力系數曲線走勢呈波動狀，原因為尾流區氣流的不穩定性較大，隨著角度的增大，迎風側與背風側的壓差也在增大，尾流出現較多分離渦，導致尾車側向力系數波動無規律.圖10(d)表明，在0°～±24°范圍內，頭車所受到的側向力最大，中車次之，尾車所受到的側向力最小，且尾車側向力系數受風向角變化的影響最小.風向角從0°變化為24°時，頭車所受側向力系數由9.4×10-5變化為0.076 9，增大了800倍，風向角為12°時整車側向力系數增大了224倍，24°時增大了500倍.根據曲線走勢，側向力系數有持續增大的趨勢，角度越大，列車越容易發生傾覆.而尾車在角度從0°變成24°時側向力系數增大的幅值為4，數值較頭車和中車而言始終最小，故尾車相對安全.

根據數據分析，對側風風向角與列車側向力系數進行三次函數曲線擬合，整車側向力系數的擬合曲線相關系數范圍為0.997 26～0.998 29，三次函數曲線表達式為：

Cz=A+Bx+Cx2+Dx3

(2)

式中：A=-0.001 37；B=0.003 83；C=4.632 24×10-6；D=2.202 78×10-6；x為側風風向角.可計算出列車在不同風向角下的側向力系數.

4 結論

(1)風向角在-12°～+12°范圍內，車身部分測點表面壓力系數的數值模擬結果和風洞試驗結果誤差范圍控制在10%以內，因此驗證了計算模型與計算方法的可行性.

(2)列車表面壓力最大處為迎風側速度來流處，且氣流通過車頭沿著車體表面向車身流動時，由于氣流方向和速度的改變，在車頭與車身連接處出現負壓區；隨風向角的增加，車頭與車身連接處的負壓程度增強，且列車表面壓力、速度分布的不對稱性增大，在列車迎風側出現大面積正壓區,背風面一側的空氣流動產生旋渦，出現較多的負壓區，車體周圍的速度也在逐漸增大；風向角從0°增大到9°，進一步增大到24°時，車體表面最大負壓值從-3 500 Pa增大到-5 169 Pa，最后增大為-9 100 Pa.

(3) 整車阻力系數與風向角的關系曲線擬合方程滿足高斯方程Cx=C0+Ae(-0.5((x-xc)/w)2)，整車阻力系數且隨著風向角的增加而相應增大，受電弓導流罩使得中車承受更大的阻力系數，故中車所受到的氣動阻力最大，尾車、頭車次之，整車的阻力系數在方向角為12°時增加了68%，24°時增大了103%.

(4) 整車側向力系數與風向角的關系曲線擬合方程滿足三次函數方程Cz=A+Bx+Cx2+Dx3，整車側向力系數的其絕對值隨風向角的增大相應增大，頭車所受到的側向力系數最大，中車和尾車次之，風向角為12°時整車側向力系數增大了224倍，風向角為24°時的整車側向力系數為0.12，增大了500倍，因此在大風向角的環境中列車有更明顯脫軌和傾覆的趨勢，應多開展列車在大風向角側風環境中的研究.