“一點”的新定義：從“數”的關聯，到“形”的變構
——2022年南通市中考新定義壓軸題的命制與再思考*

徐 強

(江蘇省南通市海門區中小學教師研修中心 226100)

2022年南通市中考數學試卷在保留南通市歷年中考數學命題“立足基礎，注重能力，注重對數學的本質和學生的數學核心素養的考查”等特色的同時，又按照教育部、江蘇省的評估報告提出的意見和近期頒發的教改、課改文件的新要求進行了優化，降低絕對難度，提高相對難度，創新相應核心知識的考查方式，充分體現“兩考合一”的功能，嚴格落實“雙減”要求，對初中數學教學起到了很好的導向作用．現將該卷中一道“一點”的代數新定義壓軸題的命制過程與反思拓展整理成文，與同行分享．

1 命制過程

1.1 立足“原則”，確定方向

按照“在傳承中求創新，在穩定中求發展”的壓軸題命題原則，繼續構建“一點”的代數新定義壓軸題，形成一道對函數單元整體考查、適度兼顧幾何知識的函數綜合題，但適當降低“概念理解”等絕對難度，難度系數為0.35～0.45．

(1)考查的內容領域與試題背景

全卷最后一題的內容領域為綜合與實踐，試題背景為“一點”新定義的數學情境，其情境表述方向為“函數圖象上點的特征”的描述．

(2)考查的主干知識與能力維度

考查的主干知識為一次函數、二次函數、反比例函數的圖象與性質，能力維度為理解概念、問題解決．

(3)考查的思想方法與核心素養

著重考查分類討論思想、方程與函數思想、數形結合思想，突出考查數學抽象、數學建模、數學運算等核心素養．

1.2 研透“傳承”，分析遷移

(1)分析特點

命題組從2019年、2021年南通市中考第26題代數新定義出發，分析其定義的特點．

(2019年南通中考第26題)定義：若實數x，y滿足x2=2y+t，y2=2x+t，且x≠y，則稱點M(x，y)為“線點”．例如，點(0，-2)和(-2，0)是“線點”．

已知：在直角坐標系xOy中，點P(m，n)．

(1)P1(3，1)和P2(-3，1)兩點中，點是“線點”；

(2)若點P是“線點”，用含t的代數式表示mn，并求t的取值范圍；

(3)若點Q(n，m)是“線點”，直線PQ分別交x軸、y軸于點A，B，當|∠POQ-∠AOB|=30°時，直接寫出t的值．

試題解讀 這道“一點”的代數新定義題聚焦一點中橫、縱坐標“數”的關聯，強化了代數推理變形的水平，從命題的角度來說是一種創新，從“新定義”的提出到“問題的設置”的命制過程凝聚了命題組全體成員的集體智慧，清晰呈現了“閱讀—理解—轉化”的模式，充分體現了“式”中思法、“圖”中求道的味道，是一道很好的考查“綜合與實踐”領域的創新試題[1]．

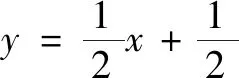
(1)分別判斷函數y=x+2，y=x2-x的圖象上是否存在“等值點”？如果存在，求出“等值點”的坐標；如果不存在，說明理由.

(3)若函數y=x2-2(x≥m)的圖象記為W1，將其沿直線x=m翻折后的圖象記為W2．當W1，W2兩部分組成的圖象上恰有2個“等值點”時，直接寫出m的取值范圍．

試題解讀 這道“一點”的代數新定義題仍體現一點中橫、縱坐標“數”的關聯，一方面盡管弱化了關系，使橫、縱坐標間的“數”的關聯更為簡潔，但整合考查了三大函數圖象及性質，從命題的角度來說又是一種創新；另一方面盡管新定義的表述很容易理解，并不在概念的理解上“為難”學生，但問題設置有著很好的區分選拔功能，同時也承載著明確的教學導向，如最后一問借助數形結合分析拋物線與直線的位置關系，需要精確畫圖、臨界分析，解題教學時教師可帶領學生全面分析出新函數圖象上“等值點”的個數．

基于以上“傳承”的思考，命題組對定義內容與方式進行了歸納，不難發現：兩年的側重點盡管有所差異，但均是“定義一個點的橫、縱坐標數量關系”，即“數”的關聯．

(2)遷移構思

基于命題方向的要求，今年仍保持從“函數圖象上點的特征”描述定義，為此，命題組從函數圖象上點的“數”的關聯出發，構思定義：函數圖象上的點到橫軸的距離等于1；函數圖象上的點到橫軸的距離不大于1；函數圖象上的點到兩坐標軸的距離同時等于1；函數圖象上的點到兩坐標軸的距離同時不大于1；……

(3)形成初稿

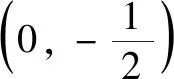
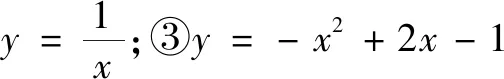
(ii)若一次函數y=mx-3m+2的圖象上存在唯一一個“近軸點”，求m的值.

(iii)若二次函數y=-(x-n)2+3n2-6n+2的圖象上存在“近軸點”，結合圖象求n的取值范圍．

分析 第1稿是在“傳承”中順勢而為，保留了2021年的定義方式，聚焦“定義”改變了設問方式．有利于考查學生對“新定義”的概念、性質、關系、規律的理解、表達與應用，注重考查學生的思維過程，避免死記硬背、機械刷題[2]．并列式三小問，難度遞增，以結構化數學知識函數(反比例、一次函數、二次函數的圖象與性質)主題為載體，分別考查了抽象能力、推理能力、運算能力、幾何直觀和空間觀念等，總體符合命題方向．

1.3 尋求“創新”，變構試題

“一點”的新定義創新點在哪兒？

(1)從“數”的關聯，到“形”的變構

在對第一稿的打磨中發現定義中的“近軸點”所屬區域相對固定，即在以原點為中心，邊長為1，且邊平行于坐標軸的正方形的區域內．學生只需找出函數與正方形的位置即可順利求解．作為全卷最后一題的壓軸題，應承載著區分選拔功能．顯然，本題的難度不足以承載選拔功能，起不到把關作用，不能讓優秀學生脫穎而出．

新定義中關鍵的是“正方形”，“形”的變構的方向一是改變“形”的形狀，即改變“到兩坐標軸的距離”的大小，如函數的圖象上的一點到橫軸的距離不大于1，同時該點到縱軸的距離不大于2，此時“形”變為“矩形”；“形”的變構的方向二是改變“形”的大小，即改變數值“1”的大小，如“1”可以變為“2”“3”“4”……

基于以上思考，命題組在初稿的基礎上，把“到兩坐標軸的距離同時小于或等于1”變成“到兩坐標軸的距離都不大于n”，讓正方形的邊長從定量到變量，增加試題區分度和難度．第2稿如下：

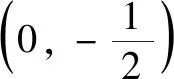
分析 此稿在初稿的基礎上，內涵更為豐富，但發現此時命名為“近軸點”不太合適，基于形的變化特點，于是將之改名為“n階方點”．試題第3稿如下：

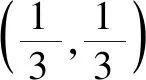
分析 定稿語言更為簡潔，“n階方點”與舉例更具啟發性，很好地滲透了特殊與一般的關系，也給人耳目一新之感！

(2)從“形”的變化，到再構試題“問題”

以上定義中關鍵的是“正方形區域的大小”隨n(n≥0)大小的變化而變化，基于此變化，命題組再構求解的“問題”，第(1)問通過“1階方點”考查反比例函數；第(2)問通過“2階方點”考查一次函數；第(3)問通過“n階方點”考查二次函數，結果如下：

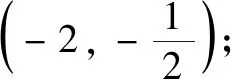
(2)若關于x的一次函數y=ax-3a+1圖象的“2階方點”有且只有一個，求a的值；

(3)若關于x的二次函數y=-(x-n)2- 2n+1圖象的“n階方點”一定存在，請直接寫出n的取值范圍．

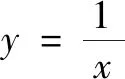
2 反思拓展

2.1 導向：教學無需大量機械訓練

作為全卷最后一題(也稱壓軸題)，仍聚焦新定義的理解與問題解決，仍以三大函數圖象及性質的內容考查為主，適當兼顧幾何知識，不僅很好地傳承了南通市“新定義”的命題風格，又在原有基礎上進行了較好的創新．這種“順勢而為”的命題方法，對落實“雙減”要求有著較好的教學導向，不給通過大量機械訓練或參加校外培訓的考生提供任何答題的便利，學生只要在課內學好學足即可．更多需要教師重視日常的解題教學，要“以題理法”，強化“新定義”的思維方式，從“數”的關聯，到“形”的變構，“以不變應萬變”.如本題定義理解教學時，要引導學生從特殊的“數”聯想特殊的“形”，從特殊的“形”聯想特殊的“數”，從而數形結合，從特殊到一般理清“定義”的本質；問題解決教學時，要引導學生畫圖，借助數形結合分析函數圖象與正方形區域的位置關系，帶領學生在變化中尋求不變，臨界分析出函數圖象上“n階方點”的個數及存在的條件．

2.2 破解：教學要從一題到一類

函數圖象上“一點”的新定義是有規律可循的，筆者以為教學時適度滲透“如何構想的方法”，不斷強化多題歸一、舉一反三，培養思維的深刻性和靈活性，這樣才能使學生從“機械操作”走向“理性思維”，從而有效突破“一遇陌生問題就一籌莫展”的軟肋．“一點”的新定義，基本類型有：

類型1 若一個函數圖象上存在橫、縱坐標的比等于n(n≥0)的點，則稱該點為這個函數圖象的“n倍點”(如2021南通市中考第26題，即n=1)．

類型2 在平面直角坐標系xOy中，若一個函數圖象上的點P(x，y)滿足x=ky+m，y=kx+m，且k≠0，x≠y，則稱點P為這個函數圖象的“線點”(如2019南通中考第26題)．

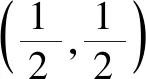
(1)下列三個函數中，圖象的“1段點”存在的有.(填序號)

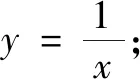
(2)若關于x的一次函數y=mx+3m+3圖象的“2段點”有且只有一個，求m的值.

(3)若關于x的二次函數y=-(x-a+1)2-2a+2圖象的“a段點”一定存在，請直接寫出a的取值范圍．

顯然，函數圖象上“一點”的新定義盡管類型有所不同，但其命題的手法一般都是構建橫、縱坐標之間的關系，“形”的變構是關鍵，如點M(x，y)—定義x，y之間的數量關系—定“形”．其考查的核心知識為數式變形，函數與方程及特殊的三角形、四邊形的性質．其注重考查的核心素養是代數推理素養——先思后變，運算推理，把握規律，關注數學知識的聯系與轉化，考查函數眼光；幾何直觀素養——先畫后算，數形結合，生成方法，關注學生思維的層次與遷移，考查建模能力[1]．

2.3 拓展：再構可從“靜態”到“動態”

“一點”新定義的再構可以從“靜態”一個點橫、縱坐標存在關聯定義，走向“動態”關于一點的變換的定義．

拓展1：平面直角坐標系xOy中，若一個函數圖象上的點P(x，y)繞點O順時針旋轉90°得點Q恰好也落在該函數圖象上，則稱點P(x，y)為該函數圖象的“內旋點”.

(1)下列函數中，存在“自對映點”的函數是.(填寫序號)

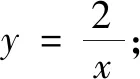
(2)函數y=2x2+3x-6的圖象上是否存在“自對映點”，若存在，求“自對映點”坐標；若不存在，說明理由.

變式1 將上題橫線處改為“關于(1，1)對稱的點”；

變式2 將上題橫線處改為“關于y=x對稱的點”．

通過“拓展”可見，命題并不神秘，關鍵還是要在研究中抓住變中不變的構題要素，如拓展的本質是“函數圖象上關于原點對稱、關于(1，1)對稱、關于y=x對稱的兩個點”，基于此可以歸于一類“函數圖象上關于某某對稱的兩個點”，如此，對試題命制角度的再思考，在重構中呈現“結構化”思維，在遷移運用中讓學生不斷增進思維的靈活性，教學也就從簡單的“模仿”走向了本質的“思考”，必將提高教學的針對性和效益．

3 結束語

“雙減”政策下用好試題資源，解讀試題“來路、思路與去路”的命制過程，研究試題命制的“有章有法”“有形有路”是“減負增效”的路徑之一，也是提高作業質效管理的需要．這不僅可以加速提升教師解題、研題、命題、教題的水平與能力，優化解題教學，而且可以大大增強日常教學教考銜接度，提高選題的精準性、作業的針對性，助推教學達成的效果．