高柔塔風電機組塔筒振源特性分析

魏煜鋒， 何維令， 蔣祥增， 何宇翔

(明陽智慧能源集團股份公司 風能研究院，廣東 中山 528437)

風力發電機組工作環境極為復雜，運行狀態下會同時受到風、大地脈動、地震等外部環境載荷以及風輪旋轉、偏航、電磁激勵等內部運行載荷的聯合激勵作用，從而導致機組的振動特性變得復雜。塔筒結構作為機組主要的支撐部件，具有輕質、高聳、低阻尼等特點，使得其對各種激勵的動力響應更為激烈，過大的振動不僅會對自身產生破壞作用，還會對機組的安全穩定性造成影響。因此，為保證機組能夠正常運行，開展塔筒在各種載荷激勵下的動力學研究具有重要意義。

目前，國內外對風電機組動力學的研究主要通過數值模擬[1-2]和模態參數識別[3-5]來實現，而對引起結構振動的誘因以及能量分布特性的研究較少。因此，為探究誘發風機結構振動的振源特性和各振源能量分布的變化規律，本文以某140 m級高柔塔風電機組塔筒為研究對象，測量其不同高度處的振動響應信號，利用譜峭度法識別誘發塔筒振動的主要振源類型及其特性，采用小波包分解和小波包能量計算原理對實測信號進行分解得到表征各振源特性的頻域分量和能量占比，最后通過對不同工況和不同測點位置的振源特性及其能量占比進行統計，得到了機組在不同工況下各測點的振源及其能量分布規律，該研究成果對機組的健康監測、安全評估以及塔架設計具有較高的實際運用和參考價值。

1 理論基礎

1.1 譜峭度

設x(n)是一組實測離散時域隨機序列，X(m)是其離散傅里葉變換。一般的，X(m)為復數序列，其二階累積量和四階累積量以共軛對形式可以定義為

k2(m)=cum[X(m),X*(m)]

(1)

k4(m)=cum[X(m),X*(m),X(m),X*(m)]

(2)

如果信號屬于穩定信號，運用復隨機變量的簡單變換得到

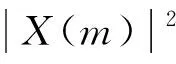
(3)

(4)

因此，頻譜的峭度值可以定義為[6]

(5)

將時間序列分為M段，并對每段分別做傅里葉變換得Xi(m),(i=1,2,…,M)，得到譜峭度的無偏估計式

(6)

線性系統的響應不會改變輸入信號的屬性。設混合信號x(n)由高斯信號和周期信號組成，即：

x(n)=b(n)+s(n)

(7)

式中：n=1,2,…,N；b(n)為高斯信號序列；s(n)為周期信號序列。b(n)經離散傅里葉變換后為B(n)，由式(6)計算出譜峭度值為

(8)

設頻率為m0的周期信號為

(9)

經離散傅里葉變換后為S(m)=Aδ(m0)ejφ，其中，δ(m0)為狄拉克函數。由式(6)可計算在m0頻率處的譜峭度值為

(10)

根據傅里葉變換的線性性質，混合信號的傅里葉變換結果為X(m)=B(m)+S(m)，得到混合信號的譜峭度值為

(11)

譜峭度法最重要的用途之一是檢驗信號中不同頻分振動的屬性，即判斷信號是具有周期屬性或隨機屬性[7]，如果信號中主要成分頻率對應的譜峭度值在-1附近波動，那么該信號整體具有周期性質，如果信號中主要成分頻率對應的譜峭度值在0附近波動，那么該信號具有隨機性質。因此，本文采用譜峭度法來檢驗塔筒振動響應信號中主要成分頻率對應的峭度值來判斷引起結構振動的主要振源類型及其頻域特性。

1.2 小波包分解和小波包能量計算

小波包分解是基于小波變換的一種信號分解精細算法，能實現對振動響應頻帶內的多層次均勻劃分，不僅具有小波變換的信號低頻部分精確分解的優點，還能同時對高頻部分進行精確分解[8]。信號通過小波包分解后，信號的全部特征信息均得以保留，從而能大大提高信號分解的完整性[9]。

假定振動信號x(t)的最高頻率為fmax，經過小波包的j層分解，可以得到2j個小波包系數[10]，其表達式如下

(12)

與這2j個小波包系數相對應的頻帶為[11]

(13)

將每個小波包系數進行重構可以得到對應的原始信號的小波包分量

(14)

因此，原始信號可以分解為2j個小波包分量的和

(15)

對于原始響應信號x(t)，j層小波包分解下的總能量Ex為[12]

(16)

利用小波包分解的正交性條件可得各個頻段總能量為

(17)

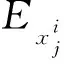
(18)

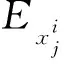
(19)

2 工程背景及實施方案

2.1 試驗機組概況

試驗機組位于河南省信陽市固始縣境內，該地區屬于平坦地形，風切變及湍流強度較小，適合高柔塔機組的穩定運行。試驗機組為半直驅式風電機組，額定功率為3.0 MW，額定轉速為11.1 r/min，切入、切出風速分別為2.5 m/s和20 m/s；機組葉輪直徑156 m，輪轂中心高度140 m，塔筒為鋼制錐筒結構，分為六節，每相鄰兩節之間通過高強度螺栓連接，從下到上各節的高度分別為17 m，17.5 m，22.5 m，25 m，27.5 m，27.42 m，塔筒總質量約為450 t，設計使用壽命為20年。

2.2 試驗系統

硬件數據采集系統采用北京東方振動和噪聲研究所研制的INV3068-S2數據采集儀以及中國地震局工程力學研究所研制的941B低頻速度拾振器；試驗數據的分析基于某開源平臺開發的分析程序。

2.3 試驗方案

整機塔筒由六節組成，在每節塔筒頂部法蘭處各設置一個測點，同時在各個測點的徑向和法向各安裝一個941B拾振器，共設置6個測點、安裝12個拾振器。將各層的傳感器通過屏蔽線纜連接到塔基的采集器上進行數據的收集，其測點布置示意圖如圖1所示。由于機組屬于高柔、低頻結構，因此將采樣頻率設置為12.8 Hz，采樣時間設置為10 min/組。

圖1 測點布置示意圖Fig.1 Schematic diagram of measuring point layout

2.4 試驗分析流程

本文根據譜峭度法與小波包分解和小波能量理論進行塔筒結構在運行狀態下的振源識別和特性分析，其流程如下：

(1)對可能引起柔塔機組振動的各類振源類型及頻率進行分析；

(2)選取三種典型工況下的塔筒振動響應數據，通過頻域分析與譜峭度法確定機組結構振動響應的主要頻率特性和主振源的屬性；

(3)對原始信號進行小波包分解，將分解的各子信號中的主頻與機組振源激勵頻率進行一一對應，確定原始信號中存在的主要振源類型；

(4)運用小波包能量原理對分解的各子信號進行能量計算，確定各類振源在振動信號中所占有的能量比重；

(5)對不同運行工況下各振源能量占比進行統計，歸納總結誘發機組振動的主要振源及其能量隨機組運行工況的變化規律。

3 振源類型及頻率分析

引起柔塔機組塔筒振動的振源類型主要分為三類，即：環境載荷激勵引起的塔筒振動、機組運行時風輪旋轉激勵引起的塔筒振動以及發電機等電磁激勵引起塔筒的振動[13]。其中，在運行狀態下對風機塔筒振動影響最為關鍵的振源是以風載荷、大地脈動為主的環境激勵以及機組運行的葉輪轉頻激勵。前者引起結構按照固有模態成分進行自激振動，后者則使風機產生周期性的受迫振動。在采集的塔筒振動響應信號中，前者體現的頻分主要為機組自身結構的低階模態——葉片、塔筒低階固有頻率，后者則體現為機組葉輪的轉頻及其倍頻成分[14-15]。

圖2(a)為利用錘擊法將葉片固定在試驗臺上測量其激勵和響應的頻響函數后通過最小二乘復頻域法(PloyLSCF)模態參數識別算法得到的柔塔葉片模態穩定圖；圖2(b)為利用塔筒振動響應數據通過隨機子空間(stochastic subspace identification,SSI)運行模態參數識別方法識別的塔筒模態穩定圖。表1給出柔塔機組運行工況下引起塔筒振動的各類振源及其頻率。

圖2 柔塔葉片及塔筒模態穩定圖Fig.2 Blade and tower modal stability diagram

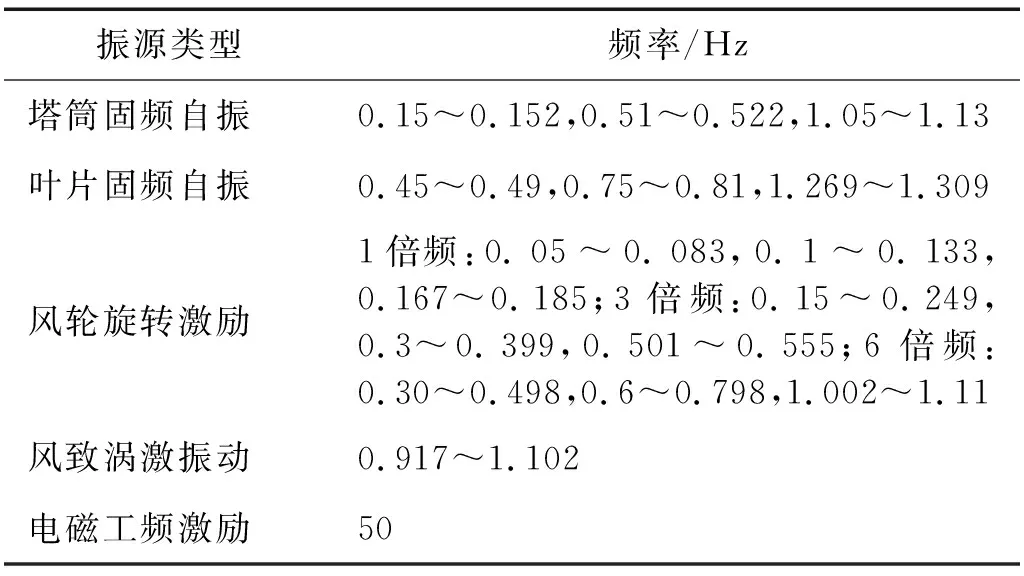
表1 振源類型及頻率表Tab.1 Vibration source types and frequencies

4 主振源識別及能量計算

4.1 譜峭度分析

表2和圖3分別給出停機、低功率、額定功率三種典型工況下機組運行參數以及對應的塔筒振動響應信號譜峭度圖。從圖3(a)中可以看出，靜止工況下，塔筒振動響應信號中的優勢頻率為0.15 Hz，體現為塔筒的1階自振頻率，對應的譜峭度值在-1附近，表明在靜止工況下，塔筒振動表現為以1階自振頻率的周期性振動；從圖3(b)中可以看出，工況2下，塔筒振動響應信號中的優勢頻率為0.095 Hz，0.15 Hz，分別體現為風輪轉頻和塔筒1階自振頻率，對應的譜峭度值都在-1附近，表明在該工況下，塔筒振動表現為以風輪轉頻以及1階自振頻率的多諧波耦合周期性振動；反觀圖3(c)中，工況3下，塔筒振動響應信號的優勢頻率為0.185 Hz，對應的譜峭度值在-1附近，表明在該工況下，塔筒振動表現為以風輪轉頻的周期性振動。

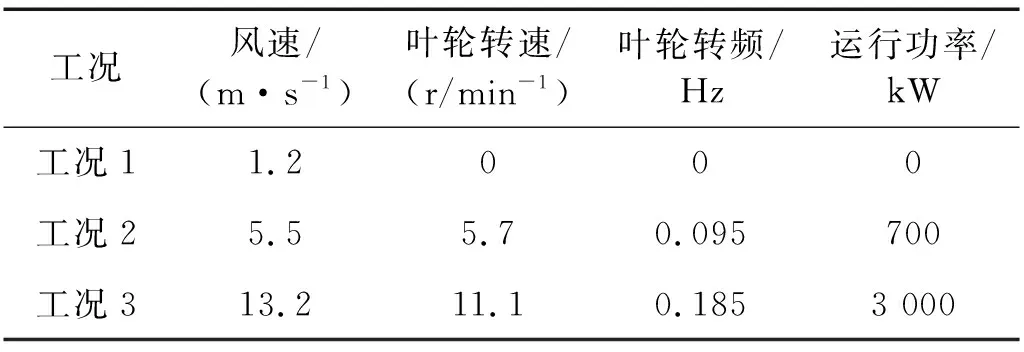
表2 三種工況參數表Tab.2 Parameter table of three working conditions

圖3 三種工況下塔筒振動響應信號譜峭度圖Fig.3 Kurtosis spectrum of tower vibration response signal under three working conditions

4.2 小波包分解和小波包能量計算

將三種工況數據進行小波包分解，由于塔筒振動響應信號具有周期性，因此小波函數為sym5[16]，分解層數為6，共分解成64個子頻帶，塔筒振動響應信號的采樣頻率為12.8 Hz，根據采樣定理[17]，fmax=6.4 Hz，每個子頻帶的帶寬為0.1 Hz。表4給出了三種工況振動響應信號小波分解和小波包能量計算后各頻帶主頻以及能量占比的統計數據，可以發現三種工況的能量主要集中在前面32個子頻帶中，達到99%以上。其中：工況1時，振動能量主要分布在的第2子頻帶中，主頻為0.15 Hz，體現為塔筒1階自振頻率，能量占比達到93.392%；工況2時，振動能量主要分別分布在第1和第2子頻帶中，對應主頻分別為0.095 Hz，0.150 Hz，體現為風輪轉頻和塔筒1階自振頻率，能量占比分別達到18.056%，64.912%；工況3時，振動能量主要分布在第2、第6、第10子頻帶中，對應主頻分別為0.185 Hz，0.556 Hz，1.109 Hz，體現為風輪1倍轉頻、3倍轉頻以及6倍轉頻，能量占比分別達到了71.016%，7.838%，18.606%。結合表2給出的風機振源類型及其對應的頻率可以看出：在工況1下，塔筒主要受自身1階自振激勵發生周期性的自激振動；工況2下，塔筒主要受自身1階自振和風輪旋轉聯合激勵發生周期性的自激、強迫耦合振動；工況3下，塔筒主要受風輪旋轉激勵發生周期性的強迫振動。

由以上分析可以得到，風機塔筒結構在三種工況下的主振源分別為塔筒1階自振激勵、1階自振和風輪旋轉聯合激勵以及風輪旋轉激勵，其中1階自振激勵頻率體現為塔筒的1階固頻，風輪旋轉激勵頻率體現為風輪的轉頻及其倍頻。

5 振源特性分析

5.1 不同工況主振源變化規律

圖4給出峭度值為-1的塔筒響應頻率隨功率、轉速變化的散點圖，從圖4(a)中可以發現：在功率約300 kW以下時譜峭度值為-1對應的頻率為0.15 Hz，體現為塔筒1階自振頻率；300～750 kW譜峭度值為-1的頻率體現為塔筒1階自振頻率以及風輪轉頻；在750 kW以上時，譜峭度值為-1對應的頻率為風輪轉頻，同時可以發現當功率達到2 000 kW以上時，譜峭度值為-1的頻率隨功率的上升不再增加，由于這時風輪達到額定轉速。從圖4(b)中可以發現同樣的規律：低轉速區(<5.5 r/min)塔筒振動響應譜峭度值為-1的頻率體現為機組塔筒的1階自振頻率；中轉速區(5.5～7.5 r/min)塔筒振動響應譜峭度值為-1的頻率體現為塔筒1階自振頻率和風輪轉頻；高轉速區(>7.5 r/min)塔筒振動響應譜峭度值為-1的頻率體現為風輪轉頻，同時可以發現在8.5～10 r/min機組設置了禁止轉速區，使風輪轉頻有效的避開了塔筒1階自振頻率。

圖4 譜峭度值為-1的頻率隨功率、轉速變化散點圖Fig.4 Scatter plot of frequency with spectral kurtosis value of -1 as a function of power and speed

圖5給出了柔塔機組在不同轉速工況下各測點主頻率的分布圖。由圖5(a)可知，在低轉速工況下，塔筒各個測點的振動主頻率分布在0.15～0.152 Hz內，表現為塔筒的1階自振頻率；隨著轉速的增大，如圖5(b)所示，各個測點振動主頻率主要分布在0.1～0.133 Hz，0.15～0.152 Hz，0.3～0.4 Hz內，分別表現為風輪1倍轉頻、塔筒1階自振頻率以及風輪3倍轉頻，同時在1.0～1.2 Hz內也有少量分布，體現為塔筒的2階自振頻率；在高轉速區,如圖5(c)，各個測點振動響應主頻率集中在0.167～0.183 Hz，0.5～0.6 Hz，1.0～1.2 Hz三個頻率范圍內，分別表現為風輪1倍轉頻、3倍轉頻、6倍轉頻，而在其他頻率區分布較少。

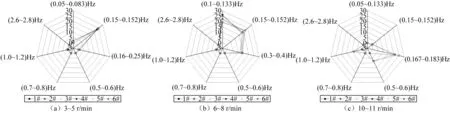
圖5 不同轉速工況下各測點響應主頻分布統計圖Fig.5 The main frequency distribution statistics diagram of the response of each measuring point under different speed conditions

根據以上分析，可知引起塔筒結構振動的主要激勵源在不同工況下表現不同，其中，在低轉速工況下，塔筒1階自振激勵為主振源；中轉速工況下，塔筒1階自振和風輪旋轉聯合激勵為主振源；在高轉速工況下，風輪旋轉的轉頻激勵為主振源，同時發現在高轉速區風輪3倍頻和6倍頻和塔筒的固有模態頻率重合，可能引起機組的共振，從表3工況3的能量分布也可看出，在3倍頻和6倍頻處對應的能量占比較大。

表3 三種工況小波包分解子帶主頻與能量占比統計表Tab.3 Three working conditions wavelet packet decomposition sub-band dominant frequency and energy ratio statistics table

5.2 不同測點各振源能量變化規律

圖6給出轉速為8 r/min、功率750 kW工況下1#、3#、5#測點振動響應信號主要振源及能量占比圖。該工況下塔筒受機組自振與風輪旋轉聯合激勵作用，圖中可以看出，風輪轉頻及倍頻、塔筒固頻自振能量占總能量的90%以上，這兩種激勵源為誘發塔筒振動的強振源。隨著塔筒位置的變化兩種強振源能量分布有所不同，隨著測點位置的降低，風輪轉頻及倍頻激勵引起塔筒振動的能量在降低，塔筒自激引起塔筒振動的能量在增加。以上表明，在該工況下，風輪旋轉激勵對塔筒上部振動影響大，機組自振激勵對塔筒下部振動影響大。

圖6 不同測點各振源能量占比圖Fig.6 Energy ratio diagram of each vibration source at different measuring points

5.3 不同工況主振源能量變化規律

圖7給出機組塔筒1#、3#、5#測點處塔筒1階自振激勵與風輪旋轉激勵的能量占比隨功率變化趨勢圖。從圖中可以看出各測點兩種主要振源能量占比隨功率變化趨勢一致，隨著機組功率的增加，塔筒1階自振激勵能量占比逐漸減少，風輪旋轉激勵能量逐漸增加。在400 kW以下時，各測點塔筒1階自振激勵能量占比高達75%以上，占據主導作用；隨著機組功率升高，在600～800 kW時，塔筒振動既受1階自振激勵影響也受風輪旋轉激勵影響，兩者對塔筒振動的貢獻相當，能量占比在30%～60%；當機組功率達到1 000 kW以上時，風輪旋轉激勵能量達到70%以上，占主導作用，并且在機組功率達到1 600 kW以上時，風輪旋轉激勵能量占比達90%以上，誘發塔筒振動的貢獻幾乎來自風輪旋轉激勵，塔筒1階自振激勵影響作用幾乎可以忽略不計。

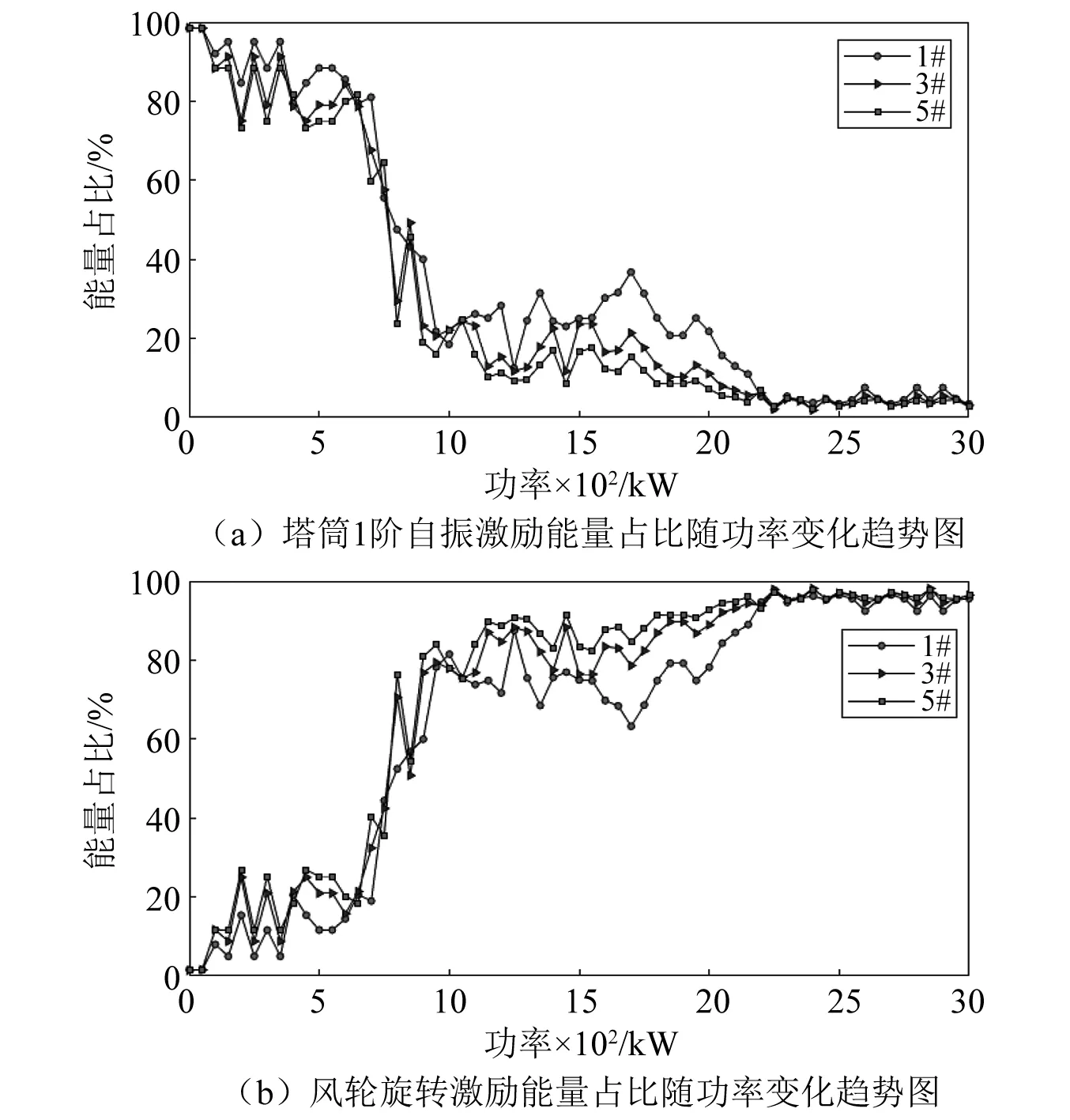
圖7 不同測點各主振源能量占比隨功率變化趨勢圖Fig.7 Trend graph of the energy ratio of each main vibration source at different measuring points vs. power

5.4 中高功率區轉頻與倍頻能量對比

圖8給出1 000 kW以上功率區各個測點轉頻激勵及倍頻激勵能量占比圖，由圖中可以看出，當功率達到1 000 kW以上時，風輪的轉頻及倍頻激勵能量占比達70%以上，由此可知中高功率區誘發塔筒振動的主要振源來自風輪旋轉激勵。其中，塔筒上部測點主要受風輪轉頻激勵作用，1倍頻激勵能量占比達60%以上，下部測點主要受6倍頻激勵作用，能量占比基本在40%～70%，遠超過1倍頻激、3倍頻勵能量占比，通過分析這一區間風輪轉速，在該功率區間，風輪轉速維持在10～11 r/min，對應的6倍轉頻為1～1.1 Hz，剛好和塔筒的2階彎曲模態頻率接近，從而引起塔筒共振，導致下部測點的振動響應在6倍頻附近能量占比很大。針對機組的安全評估，機組雖然設置了共振穿越控制程序，但主要考慮的是避免風輪轉頻(1P)和塔筒1階自振頻率重合，但實際運行中，風輪的諧波激勵對機組振動影響也較大，在高轉速區，風輪3倍頻、6倍頻與塔筒的扭轉和二階固有頻率接近，容易引發機組的共振。

圖8 中、高功率區各測點轉頻與倍頻激勵能量占比圖Fig.8 Frequency conversion and frequency doubling excitation energy proportion diagram of each measuring point in the middle and high power areas

6 結 論

高柔塔機組具有輕質、高聳、低柔等特性，使得塔筒結構對各種激勵的動力反應更為敏感。本文通過測量塔筒不同高度處的振動響應信號，基于譜峭度法和小波包分解以及小波包能量理論分析方法，從頻域和能量的角度來分析運行狀態下引起機組振動的主要振源類型及其能量變化規律，主要得到以下結論：

(1)運行狀態下機組結構振動主要受到塔筒低階自振激勵和風輪旋轉激勵影響，這兩種激勵是誘發塔筒振動的主要振源，前者頻率體現為塔筒的1階自振頻 率，后者頻率體現為風輪轉頻及倍頻。通過譜峭度分析，兩者頻率對應的峭度值都在-1附近，說明高柔塔機組塔筒在整個生命周期內始終都受到周期性的強振源激勵作用。

(2)在不同運行工況下，兩種主振源貢獻不同：在低功率、低轉速工況下，塔筒1階自振激勵為主要振源，起主導作用，風輪旋轉激勵作用影響較小；中功率、中轉速工況下，兩者貢獻相當，機組同時受到塔 筒 自振激勵和風輪旋轉激勵影響；在高功率、高轉速工況下，風輪旋轉激勵為主要振源，起主導作用，塔筒自振激勵影響較小。

(3)不同高度位置處兩種振源能量占比不同，其中，上部位置風輪旋轉激勵能量占比較大，下部位置塔筒自振激勵能量占比大。

(4)機組雖然設置了共振穿越控制程序，但主要考慮的是避免風輪轉頻(1P)和塔筒1階自振頻率重合，但實際運行中，風輪的諧波激勵對機組振動影響也較大，在高轉速區，風輪3倍頻、6倍頻與塔筒的固有頻率接近，容易引起機組的共振，影響機組的安全穩定性，因此在機組的塔筒設計時還應考慮風輪轉動倍頻與其固有頻率間的關系，適當加大塔筒結構固有頻率與風輪3倍頻和6倍頻之間的安全裕量以保障機組運行時的安全穩定性。