基于DEM與GACOS的InSAR同震形變場大氣誤差校正

白希選 張兵強 徐 昊 湛舒文 嚴 翼

1 武漢工程大學土木工程與建筑學院，武漢市雄楚大道693號，430074 2 中國科學院精密測量科學與技術創新研究院，武漢市徐東大街340號，430077 3 中國科學院大學地球與行星科學學院，北京市玉泉路19號甲，100049 4 中南民族大學資源與環境學院，武漢市民族大道182號，430074

合成孔徑雷達差分干涉測量(D-InSAR)技術是目前地表形變監測的重要手段，但雷達信號在大氣中傳播時會受到空氣中各類介質的影響，導致相位延遲或提前。對流層和電離層是大氣中造成信號延遲的主要介質層，其中對流層延遲是D-InSAR 形變測量最主要的誤差源[1-3]。D-InSAR對流層校正方法可分為兩大類，一類是通過GPS、MERIS、MODIS等外部數據建立大氣誤差模型[4-6]，如GACOS(generic atmospheric correction online service for InSAR)系統[7-9]；另一類是利用InSAR對流層延遲在時空上的統計特性，基于統計學方法來削弱其影響[10]，即擬合研究區LOS向形變相位與數字高程模型(digital elevation model，DEM)[11-13]進行誤差校正。

目前已有學者對GACOS與DEM數據在時序InSAR形變監測中大氣校正效果進行研究[10]，但是未考慮大氣噪聲與地形(相位-高程)函數中形變信號對擬合函數的影響，且不適用于同震形變觀測。施賀青等[13]基于DEM擬合相位-高程函數并降低大氣誤差，但是未考慮選擇不同擬合區域對擬合函數與校正精度的影響。本文從地震活動頻發地區選取震級MS5.4～7.0事件。首先以精河地震為例，通過研究區數據分析得到基于外部DEM進行大氣誤差校正時擬合區域的選取方法，然后以外部DEM數據分別擬合與地形相關的大氣誤差模型和GACOS數據建立的大氣誤差模型進行誤差校正；最后依據實驗結果分析兩種大氣校正方法的適用性和校正精度。

1 數據源與誤差分析

1.1 數據源

Sentinel-1A/B為C波段SAR衛星，在高緯度地區的重訪周期最短可以達到1 d[14]。本文選取10對覆蓋地震影響區域的Sentinel-1A/B衛星干涉寬幅模式(IW)雷達影像(表1)，基于GMTSAR軟件，采用兩軌法處理SAR數據。

表1 SAR數據基本信息

1.2 大氣誤差分析

大氣延遲誤差主要來源于電離層和對流層， C波段SAR衛星受電離層干擾較小，且兩次成像期間電離層延遲效應變化較小，可在數據處理過程中抵消大部分延遲信號。對流層約包含75%的大氣質量和幾乎全部的大氣水汽，天頂對流層總延遲(ZTD)可以表示為[15]:

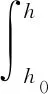
(1)

式中，Rd為干空氣氣體常數，ρ為干空氣總質量密度，Zw為可壓縮系數，Pw為水汽局部氣壓，T為大氣溫度，k1、k2、k3為大氣折射常數，h0與h分別為測站與對流層頂部對應的高程。式(1)右邊第1項為天頂靜力學延遲(ZHD)，第2項為天頂濕延遲(ZWD)，SAR影像中大氣延遲主要由對流層中濕延遲造成，引起的相位誤差可表示為：

Δφ=φ1-φ2=

(2)

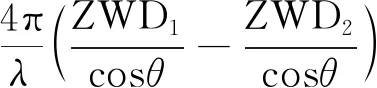
2 基于DEM數據擬合大氣誤差模型

現有研究結果表明，大氣延遲與地形具有相關性[2,10,16]。基于InSAR技術提取形變場時，通過擬合高程與形變場大氣噪聲可得到噪聲隨高程變化的函數模型，然后扣除與地形變化相關的大氣延遲信號。雖然同震形變信號遠小于高程，但一般強于大氣噪聲，擬合大氣誤差函數時若未扣除形變區域，擬合函數將受到真實形變信號的顯著影響。Albino等[16]基于DEM對形變場進行大氣誤差校正，但在擬合相位-高程函數時未分離形變信號與大氣噪聲，導致函數模型中包含真實形變信號的影響。

2.1 不同擬合區域參數分析

為避免同震形變對擬合相位-高程函數產生影響，在擬合大氣延遲信號時扣除干涉圖中有明顯同震形變條紋的區域，剩余相位解纏后的區域用于擬合兩次SAR成像期間大氣延遲信號。相位解纏共選擇13個區域，其形變邊界逐步擴大，如圖1(a)所示，其中黑色矩形表示選擇的所有實驗區相位解纏窗口，紅色矩形為擬合函數時扣除的區域，面積為1 020 km2。圖1(b)為擬合區面積與相位-高程相關系數，其中橫坐標表示擬合區面積。從圖中可以看出，精河地震區域形變信號受大氣噪聲影響較大，包含大氣噪聲的形變信號與高程具有強相關性，相關系數絕對值最低為0.839 1，最高為0.915 7，擬合區域面積為2 760 km2時達到最大值，之后緩慢下降。為避免形變信號對標準差的影響，圖1(c)、1(d)、1(e)為去除同震影響區域的大氣校正前后標準差及其差值，其中橫坐標為扣除同震影響區域后的面積。從圖中可以看出，大氣校正前后標準差隨擬合區面積增加表現出明顯的變化趨勢，擬合面積為2 350～2 760 km2時，校正后標準差降到最小值且校正前后標準差變化量趨近最大值，即此時校正效果最優。同時，從圖1(g) 、1(h)可以看出，研究區域總面積小于3 800 km2時，大氣校正后均方根下降速度較快，隨后降速變緩。

2.2 擬合區域范圍

通過§2.1分析可知，基于DEM數據擬合大氣誤差函數進行同震形變場大氣校正時，其結果主要受擬合區域影響。相位-高程函數可通過同震影響區域以外的數據擬合得到，擬合大氣誤差時在較小范圍內擴大或縮小扣除的同震影響區域(圖1(a)紅色矩形區域)對誤差函數模型與校正結果基本無影響。因此，擬合相位-高程函數時扣除的同震影響區域只需觀察干涉圖條紋進行選擇。

根據均方根、標準差及大氣校正前后同震形變對比等綜合分析可知，擬合區域面積選擇在2 300～2 800 km2時，大氣校正前后LOS向形變值與標準差、均方根變化均較為穩定，相關系數也接近幅值，可取得較好的大氣校正效果。大氣分布具有時空差異，擬合區面積大且與形變區域較遠時，大氣延遲隨高程的變化關系與形變場中心大氣分布差異性越大；擬合區面積小則相關系數低，無法準確擬合高程與形變之間的變化關系，校正后噪聲同樣較大。因此，根據校正前后均方根、標準差變化值及LOS向形變場綜合分析可知，精河地震同震形變場擬合區域面積為2 300 ～2 800km2時噪聲相對較小且變化穩定。圖2為擬合區域面積為2 350 km2和2 760 km2時大氣校正前后形變場，從圖中可以看出，LOS向最大形變量穩定在7.0～7.5 cm之間。

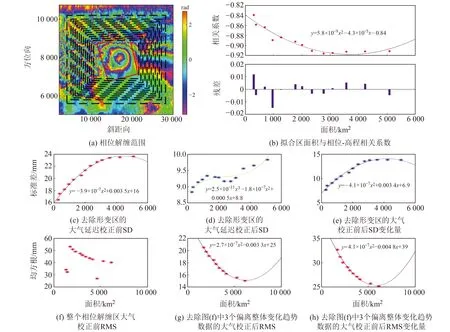
圖1 研究區與相關參數Fig.1 Study area and related parameters

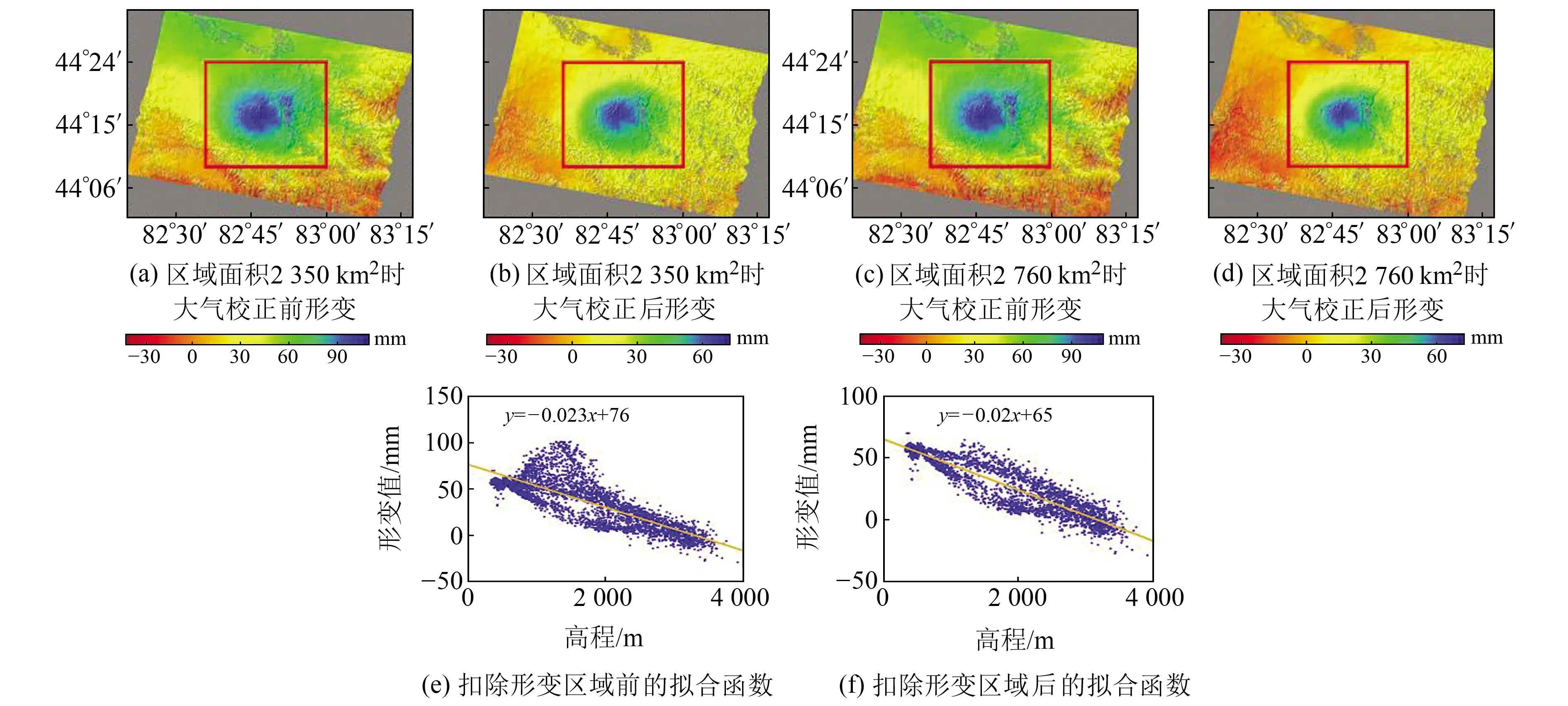
紅色矩形為擬合相位-高程相關模型時去除的區域，紅色矩形之外為擬合區域圖2 不同擬合區校正結果Fig.2 Correction results of different fitting areas

3 誤差校正分析

Albino等[16]基于GACOS與DEM數據對2017年印尼火山噴發前后形變進行大氣校正，Bekaert等[10]通過冪律函數對大氣噪聲進行校正，但上述方法均未分析研究區形變在擬合誤差函數時的影響。考慮到上述因素以及不同區域的地形差異，在對其余研究案例進行大氣校正時，以精河地震誤差函數模型的擬合區為參考，根據同震影響范圍選擇擬合區域。從數據處理結果可知，利用GACOS數據校正后的形變場可能會存在顯著趨勢，本文分別在是否設置參考點的情況下利用GACOS進行誤差校正。此外，為考慮軌道誤差造成的影響[17]，通過上述兩種方法進行大氣誤差校正后擬合并去除形變場趨勢。

3.1 基于DEM的大氣誤差校正

圖3為校正前后的形變場、誤差模型與相位-高程線性函數。表2為每個地震事件對應的相位-高程相關系數、標準差、均方根等參數。圖3(a)為拜城地震，對比校正前后的形變場可以看出，校正后幅值下降約3 cm，均方根下降2.6 cm。圖3(d)中大氣校正之前很難分辨其形變信號，然而LOS向形變與DEM相關系數達0.8，校正后噪聲大幅減小，形變量約為5 cm。圖3(e)中校正后均方根下降3.3 cm。圖3(g)中校正前斷層兩盤沿LOS向形變幅值為6 cm和-9 cm，校正后形變量為8 cm和-7 cm，噪聲下降約2 cm，比張克亮等[18]的GNSS研究結果以及楊九元等[19]的InSAR研究結果更具可靠性。圖3(i)為近海地區，與地形無關的對流層延遲信號一般較為顯著，基于DEM數據進行校正后噪聲下降相對較小。圖3中其他事件的大氣噪聲與高程相關系數較低，基于DEM進行校正后整體均方根與標準差變化微弱。

3.2 基于GACOS數據的大氣誤差校正

基于GACOS數據的校正結果如圖3中a5～j5所示，均方根及標準差等參數見表2。為提高數據處理精度，將GACOS大氣延遲信號逐像素投影至LOS向，然后分別在未設置和設置參考點的情況下進行大氣校正。未設置參考點時部分研究案例校正后噪聲反而增加，均方根增加值最大可達9 cm左右，校正后形變值可靠性低。根據形變場均值設置參考點或擬合趨勢，校正后的形變值與現有較為可靠的研究結果相近[13,18-19]。

3.3 誤差校正結果分析與討論

綜合圖3中形變場以及圖4中校正前后參數變化趨勢可知，相關系數0.45以上的地震事件基于DEM函數模型可取得較好的校正效果，均方根降幅在1～4 cm之間；相關系數大于0.8時，基于DEM數據的校正效果整體優于GACOS。由表2和圖4可知，在相位-高程相關系數低于0.4時，DEM無法擬合可靠函數模型，而利用GACOS數據進行誤差校正，均方根與標準差均下降，從形變場也可觀察到噪聲顯著下降。相關系數為0.4～0.8時，使用GACOS校正也可達到與DEM校正相近的結果，可以使用兩種方法相互驗證。因此，基于兩類數據進行大氣誤差校正時可以互補，噪聲與高程相關性越強，說明地形越復雜且存在顯著大氣噪聲，此時GACOS數據受GNSS站密度與ECMWF(European centre for medium-range weather forecasts)等數據源精度影響，校正精度相對較低；而相關性越強，說明噪聲分布更依賴于高程，只使用DEM擬合大氣誤差函數可獲得更為精確的結果。

4 結 語

本文以大氣噪聲顯著的精河地震為例，建立基于DEM進行大氣誤差校正時擬合區的選取方法；然后分別基于DEM和GACOS建立的誤差模型對不同地區與震級事件的LOS向形變數據進行校正，并分析校正精度和不同方法的適用性，得到以下結果：

表2 研究區大氣校正前后相關參數

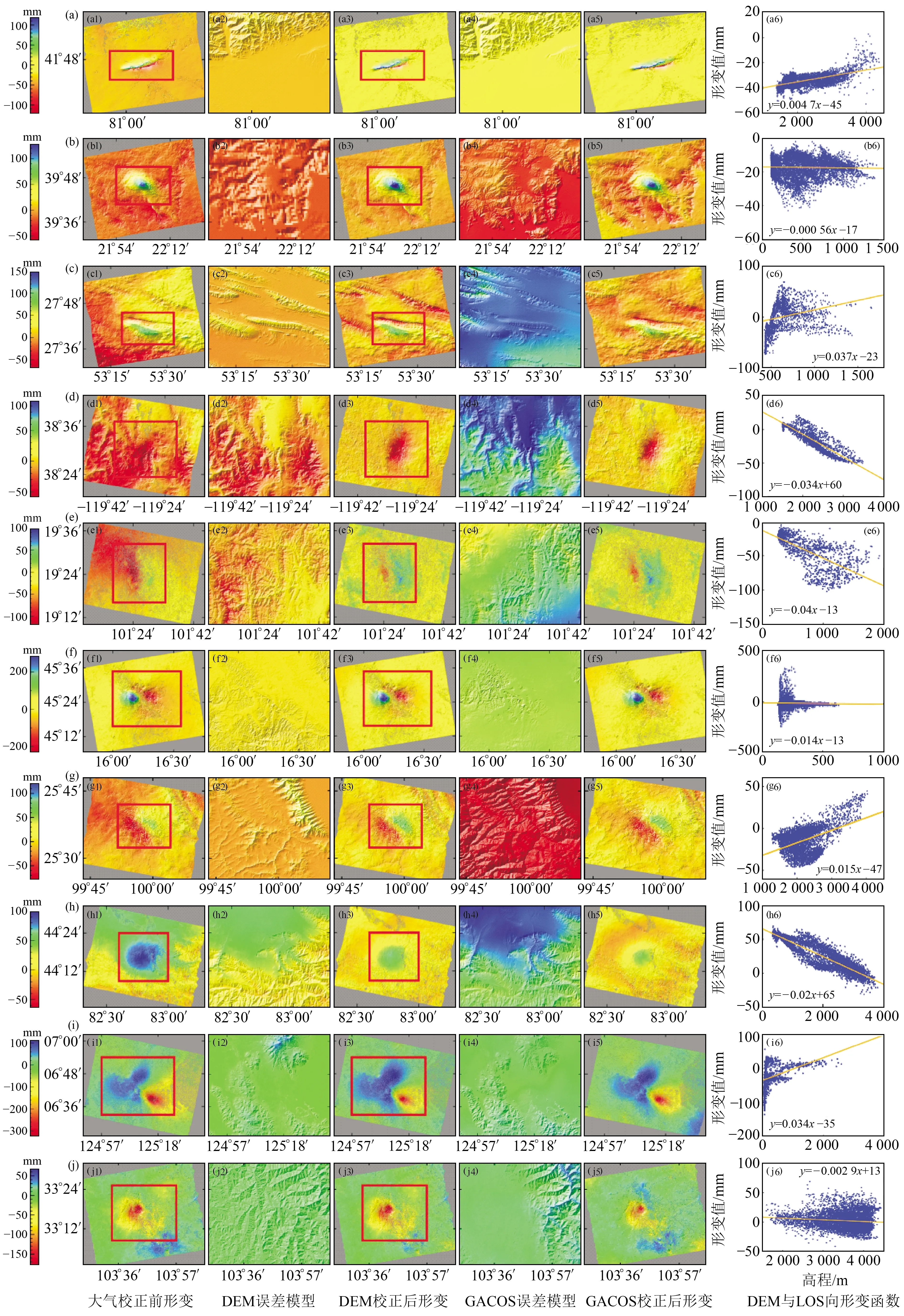
圖中a～j依次為表1中序號1～10對應的地震事件；圖中紅色矩形為擬合相位-高程函數時扣除的主要同震影響區域，矩形以外為擬合區圖3 基于DEM和GACOS數據大氣延遲校正Fig.3 Atmospheric delay correction based on DEM and GACOS data

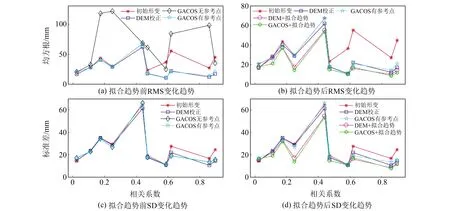
(c)中有無參考點對應的標準差一致，因此只體現出3組數據圖4 大氣校正前后參數隨相關性變化趨勢Fig.4 Variation trend of parameters with correlation before and after atmospheric correction

1)考慮到不同發震區域地形差異以及擬合區與形變區大氣延遲的空間差異性，基于DEM擬合大氣誤差模型時，最佳擬合區并非固定值，在一定范圍內均可取得較好的大氣校正結果。以精河地震為例，相位-高程相關系數絕對值臨近最大值且擬合區域面積在2 300～2 800 km2范圍內時，校正效果整體較好。因此，本文未給出通過多次實驗確定擬合面積的計算方程，而是給出相關性與校正精度隨擬合區面積的變化趨勢，以供擬合誤差函數時參考。

2)相位-高程相關系數絕對值大于0.4時，必須考慮大氣誤差對形變值的影響；相關系數小于0.4時，噪聲受高程影響較小，可基于GACOS進行誤差校正；相關系數為0.4～0.8時，可使用兩種校正方法相互驗證；相關系數大于0.8時，基于DEM校正后的均方根與標準差均低于GACOS，強相關性也表明形變場噪聲分布顯著依賴于高程，可單獨基于DEM擬合噪聲分布模型。

3)在本文所有研究案例中，基于上述兩種方法校正的數據結果在消除趨勢后均方根與標準差整體下降，因此，大氣校正后可通過對形變場進行多項式擬合以消除部分趨勢。