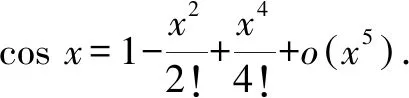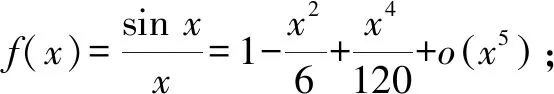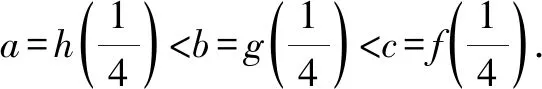借助思維導圖將思維“可視化”,解決壓軸題
——以2022全國甲卷第12題為例
楊 東 李洪全 姜遠航
成都七中 石室天府中學
學生在面對思維需求量較大的題目時,往往具有一定的困難.而借助思維導圖將思考過程可視化,可以幫助他們更好地呈現思維過程,厘清邏輯的基本關系.這里,筆者以2022年全國甲卷第12題為例,來探索思維如何在清晰的流程中得以更好地展示出來.
1 題目呈現
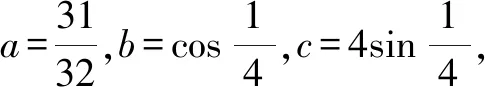
A.c>b>aB.b>a>c
C.a>b>cD.a>c>b
本題為2022年全國高考理科甲卷第12題(選擇題最后一題),是一個典型的比較大小的問題,這類問題不僅充分考查學生對知識的綜合應用,而且對數學方法的選取也會顯得多種多樣.下面提供幾種解法,供大家討論.
2 解法分析及詳解
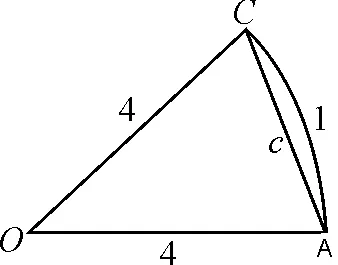
2.1 b與c的大小比較
首先我們注意到b,c兩個數中,有非常顯眼的數字“4”,因此可通過構造函數將這個固定的“4”變為一個變量,這是構造函數中非常典型的一種處理方式.另一方面,如果挖掘三角函數的特性,也可以考慮將角的三角函數,用幾何方法構建出來.試著解決這個比較大小問題.我們通過思維導圖,將下列三種解法呈現出來.
下面分別通過代數思路分析方式和幾何思路分析方式來呈現幾種解法,以期望能夠更好更清晰地表達出解決問題的突破口和思考方式.
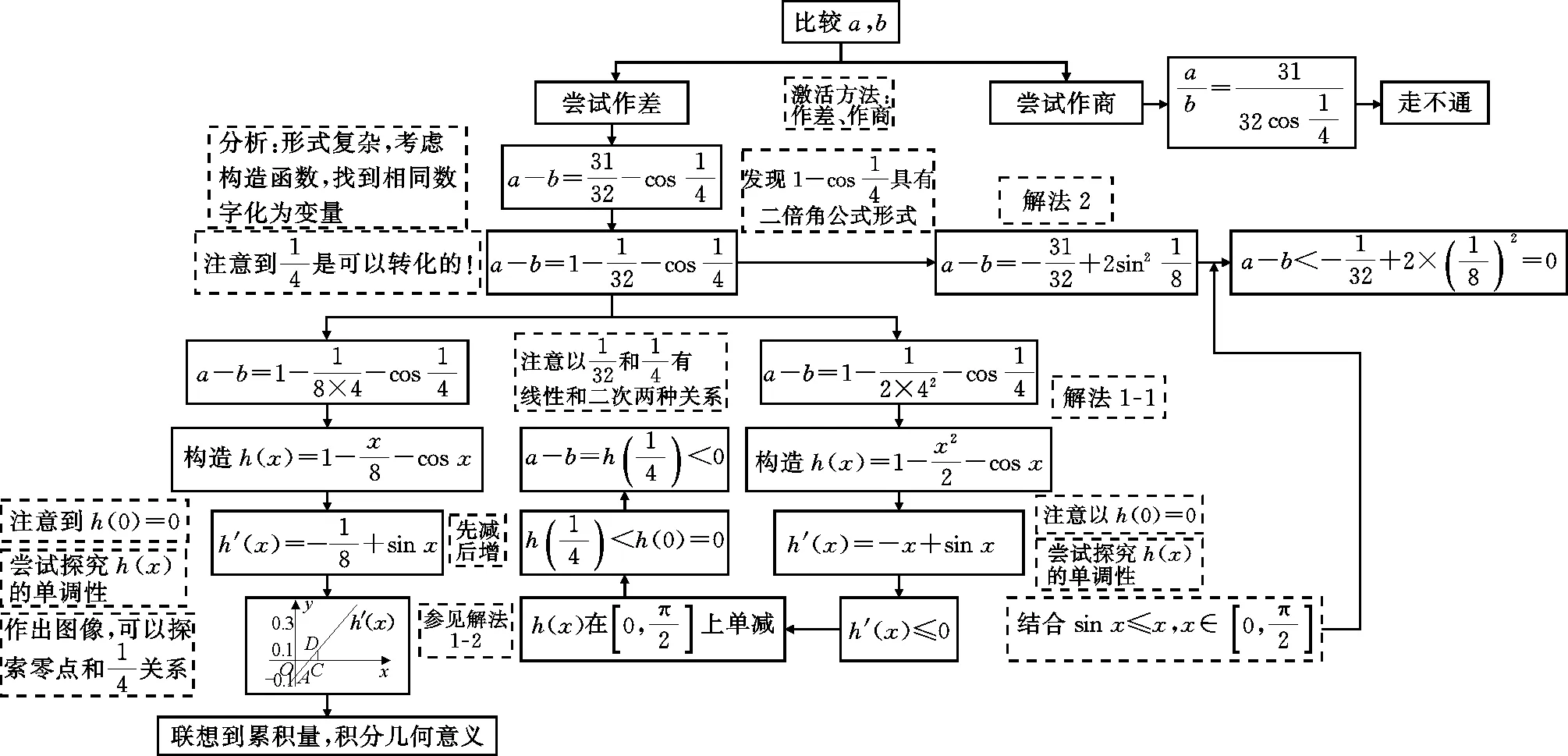
代數思路思維導圖,如圖1所示:
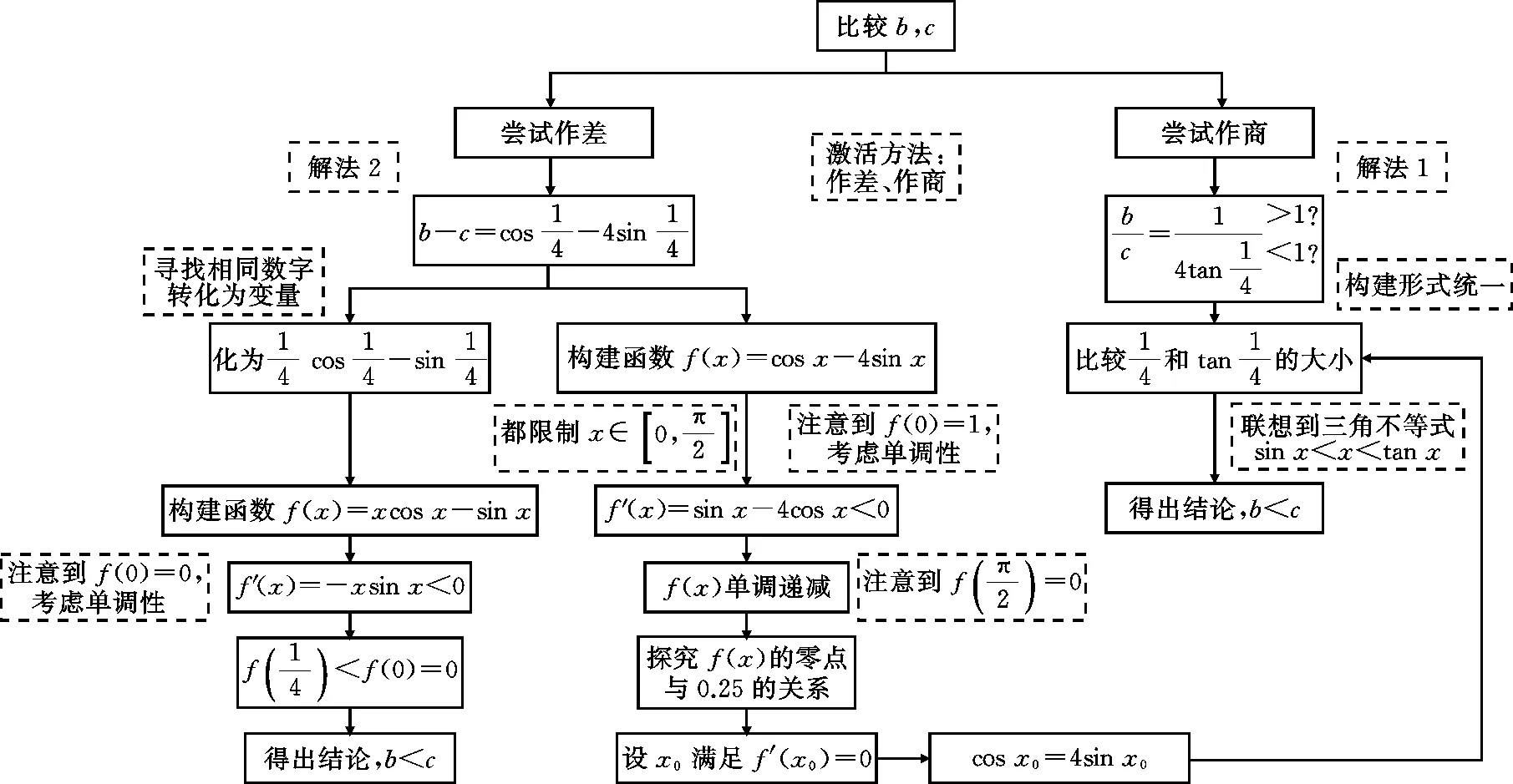
圖1
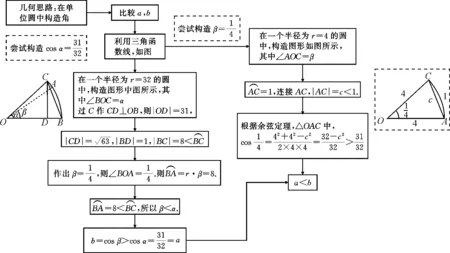
幾何思路思維導圖,如圖2所示:
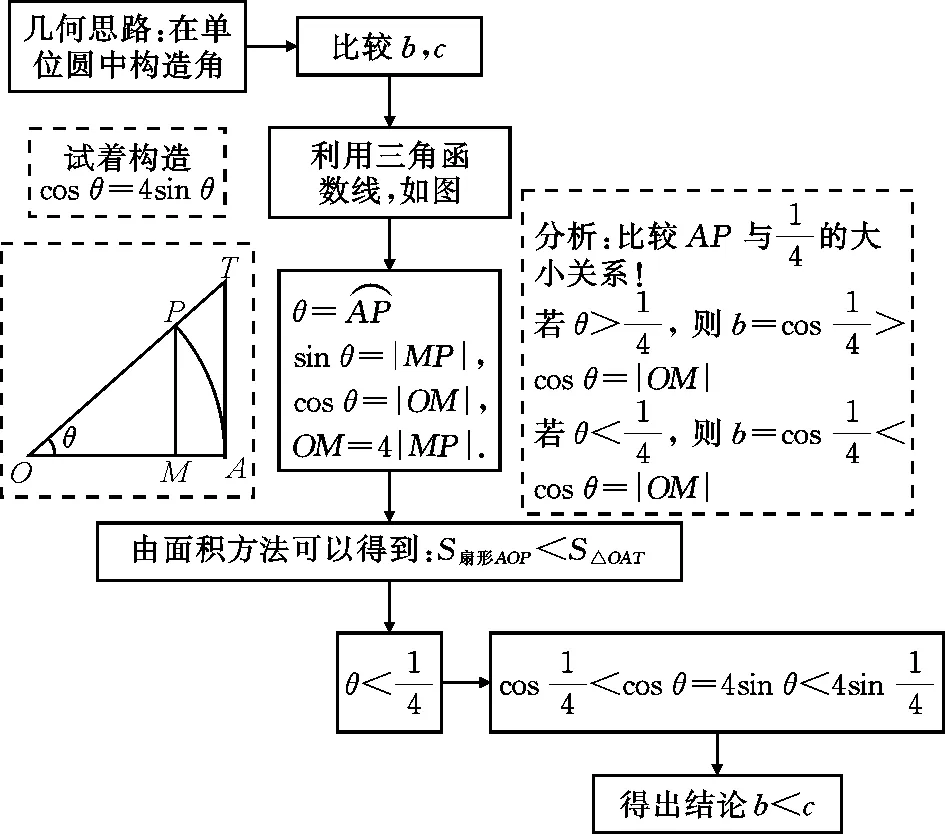
圖2
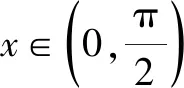
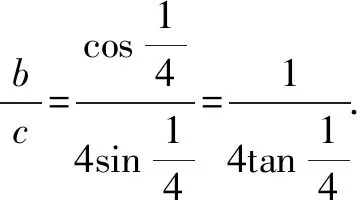
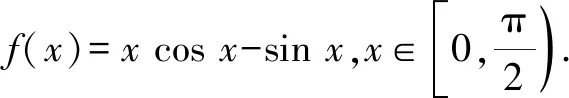
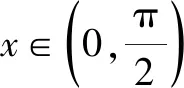
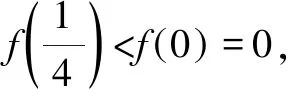
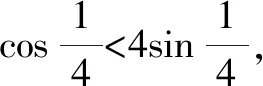
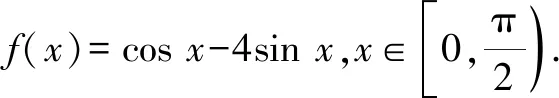
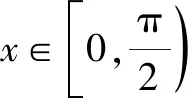
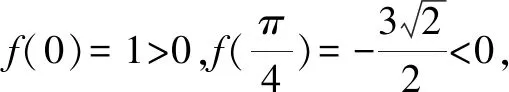
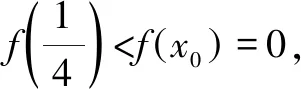
所以b 圖3 以上三種解法中,解法1是常規的通過兩式比值與1的大小來判斷,具有普遍性,是我們首先可以想到的方法. 第二種解法是構造函數,也是對不同式子中的相同量加以抽象把握得到的函數模型.而解法2中提到的兩種函數構造方法,其實告訴我們即使不是一次性就選出最優的函數模型(實際問題中也往往不可能一眼就選出最優解),通過合理的分析也能夠找到解決問題的途徑. 下面利用思維導圖將思維過程可視化.如圖4所示: 圖4 同樣地,通過回歸教材,利用幾何方法加以思考,可以得到如圖5所示的思維導圖: 圖5 解法1-1:構造二次函數. 而對于構造一次函數形式,將通過后面的解法1-2進行更深入的介紹. 解法2:發現二倍角關系. 解法3-1:利用單位圓將特殊值三角函數化. 圖6 圖7 故a 圖8 通過進一步挖掘試題背景,發現這個題目中有很明顯的多項式與三角函數的替代關系.如果具備一定的級數知識基礎,那么很快會發現,此題目其實具有麥克勞林級數的特點,只需要把sinx和cosx在原點處展開,可以瞬間解決這個問題.過程如下. 已知以下麥克勞林展開式: 故a
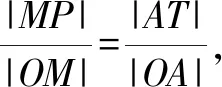
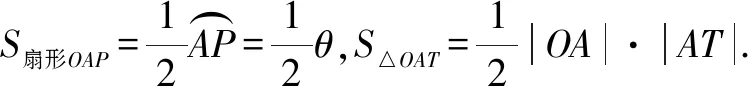
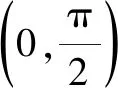
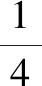
2.2 a與b的大小比較
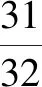
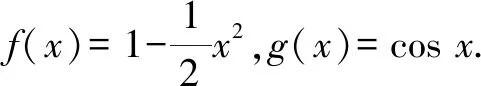
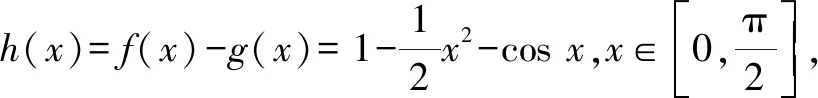
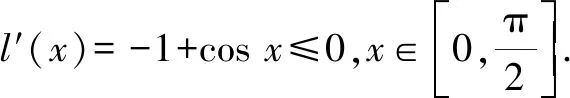
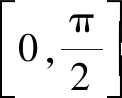
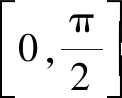

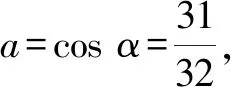
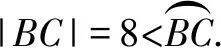
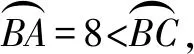
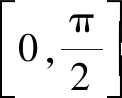
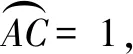
3 深挖題目背景,借助大學先修知識來解決問題
3.1 利用積分處理a,b的一次函數構造比較
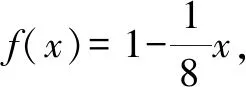
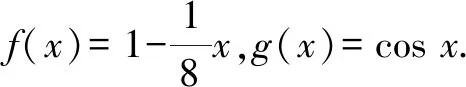
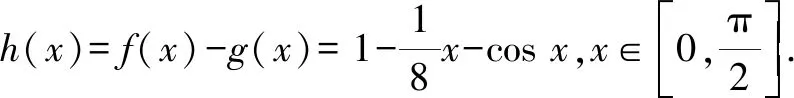
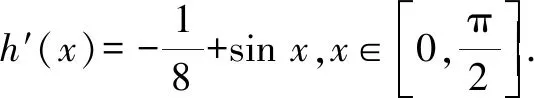
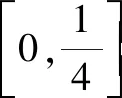
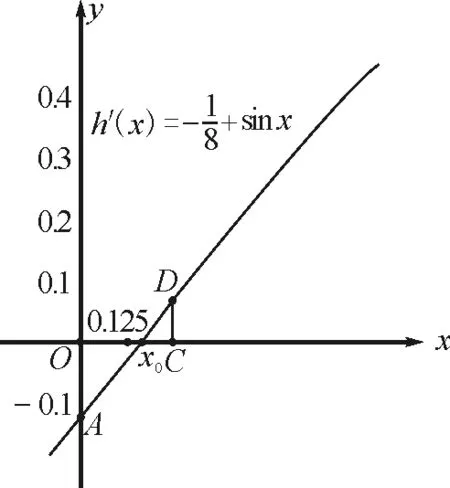
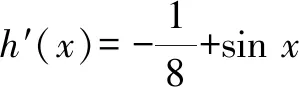
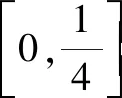
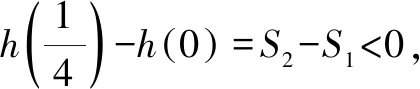
3.2 利用泰勒展開式對a,b,c的大小判斷一步到位