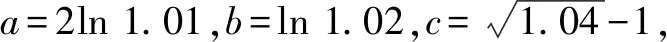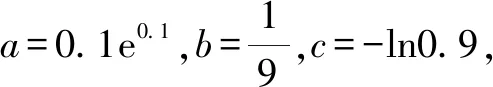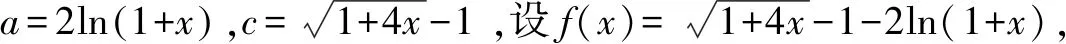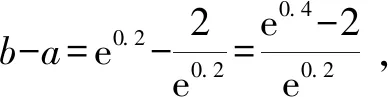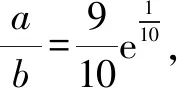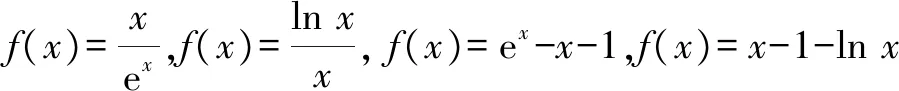指對冪數大小比較的解題策略
宋凱東
江蘇省啟東市第一中學
新高考數學重視對學生基本數學素養、思想方法與能力的考查,關注學生應用意識與創新意識.指對冪數式大小的比較常運用到邏輯推理、數學建模、數學運算等核心能力.從題目的難度上看有基本題也有壓軸題,從解題技巧上分析有常見的方法也有一些創新的方法,所以一方面需要學生掌握一些常規技巧,另一方面又需要打破常規思路,發散性地思考問題,提升解決問題的能力.
1 應用橋梁法比較大小
應用策略:先將各數化成同底數或同指數形式,再確定所要考查的指對冪函數類型,根據底數或同冪情況判斷已確定函數的單調性,從而得出大小關系.
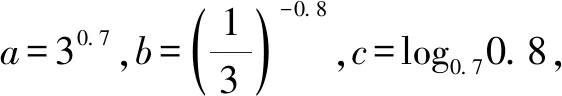
A.a C.b A.c C.a 上述例1中,a與b兩個數可以化為同底數3,利用冪函數的單調性可以直接比較,得1 評注:能使用橋梁法比較大小的,一般難度不會太大.當其中兩個數式直接比較大小困難時,我們可以嘗試利用一個中間量介入,起一個橋梁作用.這個中間量選取要根據具體題目的需要,有些題中已提供,而沒有提供的,一般先考慮最常見的0或1.當然一些較難的題目,可能選取的中間量過程也比較復雜,要多觀察題目中數式的大致特點,經過適當的轉化,以選取到合適的數式. 應用策略:作差、作商法一般適用于當底數與指數都不相同時,選取適當的媒介數,首先考慮化為同底數,求同存異.作差法是將要比較的兩個數作差,再根據差值與0的大小作比較;作商法是將兩值作商,根據其值與1的大小關系,從而確定所比值的大小. 例3設x,y,z為正數,且2x=3y=5z,則( )[1]. A.2x<3y<5zB.5z<2x<3y C.3y<5z<2xD.3y<2x<5z 例4(2020全國Ⅲ,理12)已知55<84,134<85.設a=log53,b=log85,c=log138,則( ). A.a C.b 因為ln 3+ln 8=ln 24<2ln 5 ,所以a 評注:作差、作商法比較兩個數式大小,在初中數學教材中就已出現,是比較兩個數大小最常見的方法.在高中數學中使用此方法時,還須加入式子的變形與轉化這一步驟,而恰恰這一步也是學生感覺最難處理的一步.因此在平時的訓練中應加強對不同底或不同指數化成相同數的訓練,常用的方法是使用換底公式和等式兩邊取同底對數. 應用策略:在構造函數時要根據題目條件的特點進行猜想,在構造時多進行試驗與數式的調整.根據構造出的函數求出其單調性,有時還需利用函數的對稱性、奇偶性、周期性把幾個數式化到同一單調區間[2]. 例5(2020全國II卷,11)若2x-2y<3-x-3-y,則( ). A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0 A.a C.a 例5中,將條件中的不等式變形成2x-3-x<2y-3-y,很明顯可構造出函數f(x)=2x-3-x,則f(x) A.a C.b 例8設a=2e-0.2,b=e0.2,c=1.2,則( ). A.a C.b A.a C.c 例9非常難,小題不小,不亞于函導數的一道大題.關鍵在兩處地方,變形后構造了兩個不同的函數和兩次求導,并且綜合使用了比差法與比商法. 隨著新課程改革的不斷深入,高考數學試題的內容及呈現形式也在不斷發生變化.高考題目不斷翻新且難度加大,并且考查的能力要求不斷加強.總體來看,高考命題向寬角度、多視點、多層次的趨勢發展,注重“雙基”考查的同時,對學生運用知識的靈活性及推理與運算能力提出了較高的要求.縱觀近幾年高考數學,比較指對冪數大小的題目類型千變萬化,惟有與時俱進地加強分析研究,在平時的教學中不斷深化教法、學法,強化數學基本思維,幫助學生學會思考學會類比,才能以不變應萬變,提高解題能力.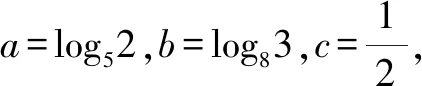
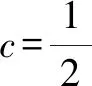
2 應用作差及作商法
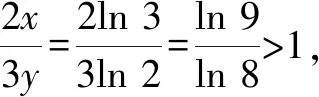
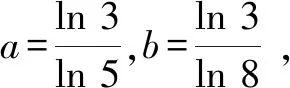
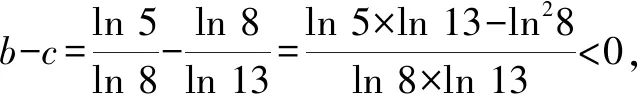
3 應用建構函數法
3.1 構造同一函數
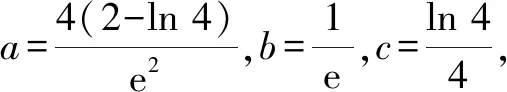
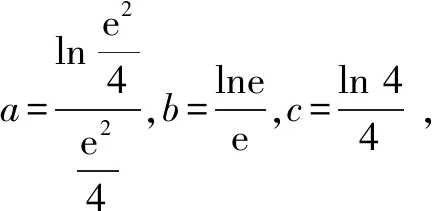
3.2 構造不同函數