創新解題方法 培養創新能力
——以一道比較大小的選擇壓軸題為例
操厚亮
湖北隨州二中
《普通高中數學課程標準(2017年版)》提出“四能”,即發現問題、提出問題、分析問題、解決問題的能力的總目標.數學中的創新往往始于問題,發現問題是創新的基礎.數學家們常說:發現問題往往比結論更重要.因此,教師應適時、適度引導學生發現、提出一些數學問題,進而分析和解決問題,培養學生的數學學科核心素養和創新能力.
1 試題呈現
A.a C.a 觀察四個數,不難發現0.1這個數高頻出現,可以嘗試構造函數,自變量x在包含0.1的一個區間內,如果這些函數在該區間內大小關系確定,那么在x=0.1處的函數值大小關系也確定.這體現了數學中的一種共性與個性的關系,一般與特殊的數學思想方法. 解法一:構造函數+放縮法. 故d(0.1)-b(0.1)>d(0)-b(0)=0,即d>b. f′(x)=ex(cos2x-sin 2x) =ex(-sin2x-sin 2x+1). 設g(x)=x-sinx,則g′(x)=1-cosx≥0,從而g(x)=x-sinx為增函數. 所以x∈[0,0.1]時,g(x)≥g(0)=0,即x≥sinx. 故f′(x)≥ex(-x2-2x+1)=ex[-(x+1)2+2],當x∈[0,0.1]時f′(x)>0,f(x)=excos2x-1為增函數,有f(x)≥excos20-1=0,從而當x∈[0,0.1]時,y=b(x)-c(x)為增函數. 故b(0.1)-c(0.1)>b(0)-c(0)=0,即b>c. 綜上,d>b>c>a. 由解法一不難發現,上述構造的這些函數是常見的函數,借助圖象,觀察圖象的上下關系進而比較數值間的大小關系,優化解法一則得下面的解法二. 解法二:圖象+構造函數+放縮法. 圖1 設f(x)=sinx-(ex-1)cosx,則 f(0)=0,f′(x)=(ex-1)(sinx-cosx). 于是tanx 故a 由解法二不難發現,這些構造的函數圖象比較相似,接近冪函數在區間(0,1)上的圖象,由此聯想泰勒展公式的功能,可以借助泰勒展開式來估算. 推薦理由:本書輯錄了著名經濟學家厲以寧從中國改革開放至今的40篇代表性論文,篇目由厲以寧先生親自審定。內容主要涉及中國經濟體制改革,中國在經濟發展過程中的探索與創新,中國經濟的機遇與挑戰,中國的農業、工業改革,以及與經濟發展密切相關的教育、管理等方面的見解。這些文章都是厲以寧對中國經濟發展時期的精辟論斷,是他對中國經濟自改革開放以來40年的不間斷思考與研究精華,對中國今后的經濟改革與發展具有重要的啟示意義。 評:本題還可以用[2,2]階帕德逼近來比較大小,但帕德逼近相對泰勒展開式來講是一種精度更高的分式函數逼近,此處略去.有興趣的讀者可自行研究. 繼續觀察構造的這些函數的圖象,不難發現,這些函數在0處的函數值均相同,不同的是其增長速度快慢有別.那么通過增長速度的快慢比較大小是一種創新的解法,到此完美突破難點. 解法四:研究函數在x=0處的增長速度,通過增長速度快慢比大小. 設g(x)=ex-1,則b=g(0.1). 設h(x)=tanx,則c=h(0.1). 又f(0)=g(0)=h(0)=k(0), 所以d最大. 又f″(0)≤h″(0)≤g″(0),所以a 綜上可知,d>b>c>a. A.a C.c A.a C.c C.x>yD.2ex>y 答案:(1)C; (2)B; (3)D. 眾所周知,比較大小的試題每年高考都有出現,尤其是近兩年,精度越來越高,難度越來越大,方法越來越靈活多樣.作差、作商、插值,以及簡單的構造函數利用單調性比較已經不能解決變化著的新問題.如何快速突破此類問題刻不容緩,必備基本功除了不等式的性質、基本不等式,還需要熟悉常見的不等式,如,糖水不等式、對數糖水不等式、泰勒展開式(函數不等式:切線放縮、曲線放縮等),了解帕德逼近等知識.對本道題而言,容易想到的方法是構造函數作差求最值比較大小,體現了一般到特殊的思想方法,對用導數的方法研究最值和計算求解能力要求較高,而用泰勒展開式和帕德逼近來估算的話,思維降維了,但站位較高,這些都是高等數學里的知識.但通過函數在某點處的增長速度來比較大小確實是一種創新解法,學生易接受. 在函數與導數教學與學習的過程中,對一些難題,應微專題分析,引導學生觀察發現問題,不斷創新解題方法,進而培養學生的探究與創新精神.Z2 觀察發現問題,不斷創新解法,培養創新能力
2.1 觀察發現1
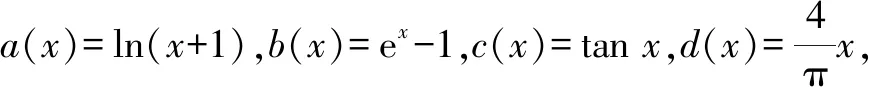
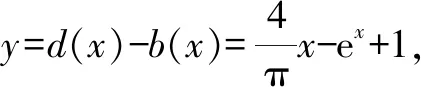

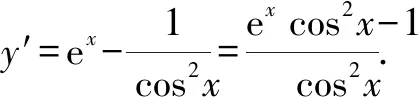
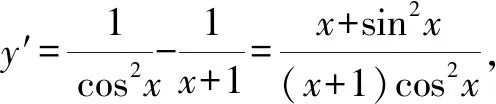
2.2 觀察發現2
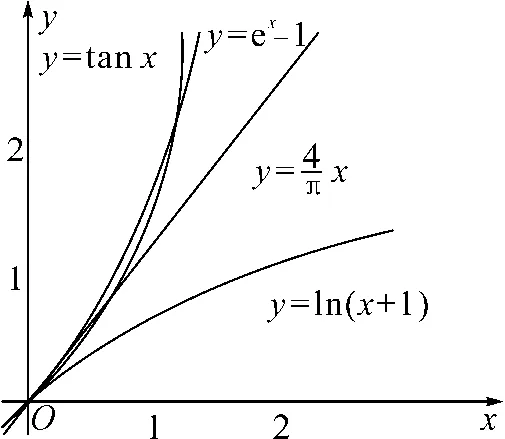
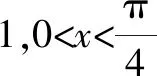
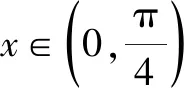
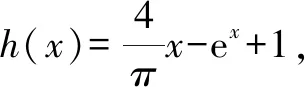
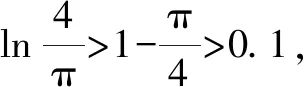
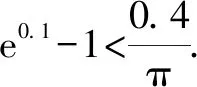
2.3 觀察發現3
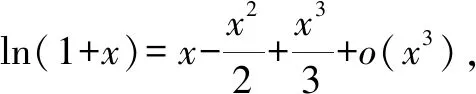
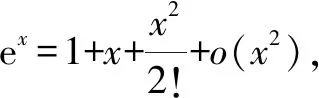
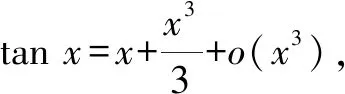
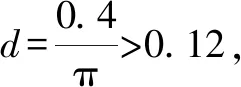
2.4 觀察發現4
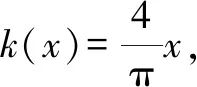
3 鞏固提高
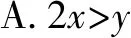
4 結束語

