巧構函數 妙判大小
——2021年高考數學乙卷理科第12題的評析
崔 娟 李象林 張春寧
山東省淄博實驗中學
代數式的大小比較問題,合理融合并交匯了函數的圖象與性質、不等式的基本性質等內容,充分落實新課標中“在知識交匯點處命題”的指導思想,是近年高考數學命題中的一大基本考點,常考常新,形式多樣,變化多端.下面結合2021年高考數學乙卷理科第12題這道代數式的大小比較判斷來分析.
1 真題呈現
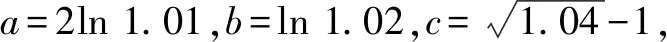
A.a C.b 該高考試題一改常態,無法直接結合題目中對應的代數式來明確構造對應的函數,需結合相應的代數運算與恒等變形,借助所構造函數的圖象與性質及一些基本比較方法來分析與處理. 通過分析,尋找1.01,1.02,1.04之間的規律,可以轉化為1+0.01,1+0.02,1+0.04,建立參數1+x,1+2x,1+4x,通過作差比較法,合理構造復合型函數,利用求導判斷函數的單調性來分析與處理. 該題創新新穎,難度較大.從部分考生的反映來看,錯誤率非常高.大部分考生無法判斷,任意作出一個選擇.下面就該代數式的大小比較加以合理精彩解析,展開一幅美麗的畫卷. 方法1:構造函數法. 則有a=2ln 1.01=ln 1.012=ln 1.020 1>ln 1.02=b,即a>b. 所以f(x)>0,即a>c. 所以h(x)<0,即c>b. 綜上分析,可得a>c>b. 故選擇答案:B. 點評:要判別三個代數式之間的大小關系,要進行三次比較,在比較a與b的大小關系中,可以利用對數函數的基本性質來判斷;而比較a與c,b與c的大小關系中,分別通過不同函數的構造,利用換元方法,并結合求導處理,利用導函數在給定區間上的正負取值判斷單調性,進而確定給定區間上的函數的正負取值,得以判斷對應的代數式大小關系.無法直接利用不等式的性質來比較大小時,經常借助函數的構造來巧妙處理. 方法2:構造函數法的改進版. 那么,函數f(x)在區間[0,2)上單調遞增,則有f(0.01)>f(0)=0. 則有a>c,可以排除選項C. 綜上分析,可知b 故選擇答案:B. 點評:利用對數函數的基本性質來判斷a與b的大小關系后,可以根據選項的排除與分析,只要再比較a與c的大小關系即可得以正確判斷.在判斷a與c的大小關系時,通過構造函數,利用導函數在給定區間上的正負取值判斷單調性,結合單調性的應用,得以判斷a與c所對應的代數式大小關系.合理借助選項之間的關系,邊判別邊優化,節約時間,提升解題效率. 方法3:導數對應的增長速度判別法. 顯然有f(0)=g(0)=h(0)=0,且a=f(0.01),b=g(0.01),c=h(0.01). 所以g′(x) g(0.01) 所以b 故選擇答案:B. 點評:利用三個代數式之間的關系構造與之對應的函數,通過求導,進而判斷在對應的區間上導函數之間的大小關系,結合導函數的幾何意義所對應的函數的增長速度,得以判斷對應的代數式大小關系.利用導數對應的增長速度判別法來處理,關鍵是要熟悉導數的幾何意義,技巧性強,能力要求高. 方法4:泰勒公式法. 解析:根據泰勒公式,得 由以上a,b,c的展開式可知b 故選擇答案:B. 點評:泰勒公式是高等數學中的相關內容,屬于高中數學的知識拓展與課外提升部分,也是高中數學競賽常備知識點.借助泰勒公式的展開,并結合三個代數式在泰勒公式條件下的進一步轉化,可以很好比較大小.泰勒公式法只是作為參加數學競賽的部分考生的一種快速判斷方法,一般學生有一個大體的了解即可. 涉及代數式的大小比較問題,主要考查基本初等函數的變形與運算,以及對應函數的圖象與性質,經常以冪函數、指數函數或對數函數為主,或單獨一個函數,或多個函數的差(或商).經常利用構造函數法、比較法(作差或作商)、特殊值等常規通技通法來分析與處理. 在代數式的大小比較問題中,經常結合代數式的特征以及代數式的作差(作商)運算等,合理構建冪函數、指數函數或對數函數等基本初等函數.在合理構建函數的基礎上,或直接利用函數的圖象與性質法來處理,形象直觀判定;或通過函數求導,利用函數的單調性等性質來處理.其中要重視運算轉化,導數工具性應用等. 涉及代數式的大小比較問題,能很好承載數學知識、數學思想方法和數學能力等,其比較過程就是一個數學知識、思想方法和能力的交匯與融合的過程,借助這個過程很好滲透特殊值法、特殊判定法、特殊圖象法等方法的應用,以及數學抽象、邏輯推理、數學運算等相關的數學核心素養的培養.Z2 試題分析
3 真題破解
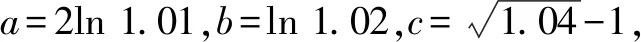
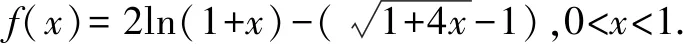
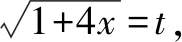
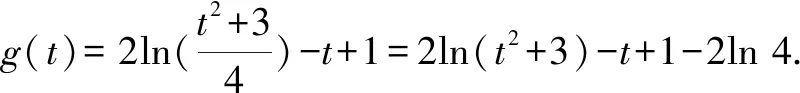
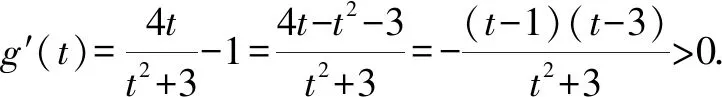
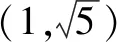
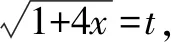
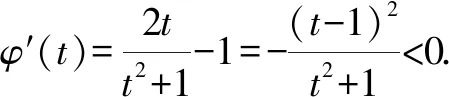
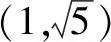

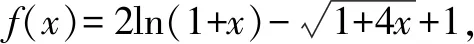
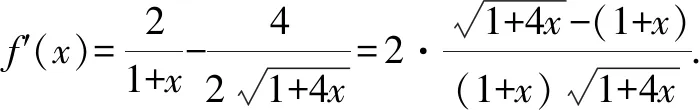
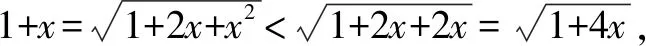
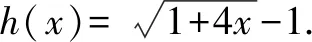
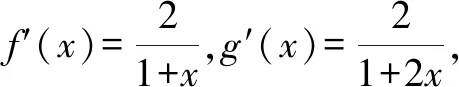
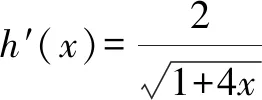
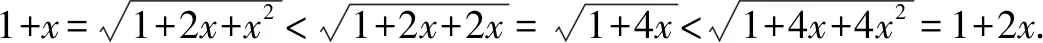
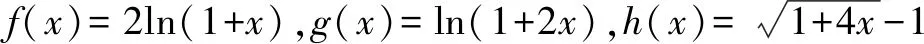
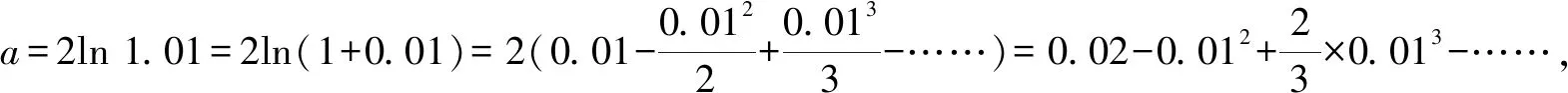
4 教學啟示
4.1 鞏固“三基”訓練,掌握通技通法
4.2 重視“函數”構建并形成方法體系
4.3 體驗過程感悟,培養核心素養

