活用數學教材 挖掘習題特質
——以一道課本習題探究一類指數型分式函數的對稱中心
2023-02-11 03:31:56唐新陽
中學數學雜志 2023年1期
唐新陽
湖南省寧鄉市第一高級中學
1 問題的提出
人教版各版教材的復習參考題中都有一道以下習題:
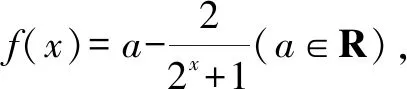
該習題在2019版的人教版教科書必修第一冊第161頁依然編入,可以看出歷任編者對該道習題的情有獨鐘.結合新教材第87頁關于函數對稱中心問題的研究,本文中以該習題為例探究一類指數型分式函數的對稱中心.
2 問題的初探
關于奇偶性的討論,注意到函數定義域為R,可以有較多方式探究.此處僅以奇偶性定義求解.

3 問題的引申與探究
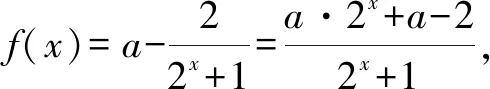
3.1 直接求解
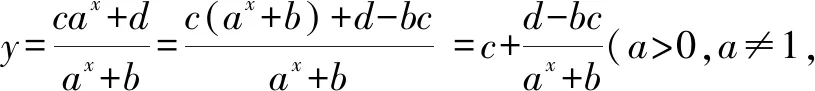
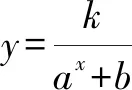
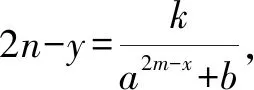
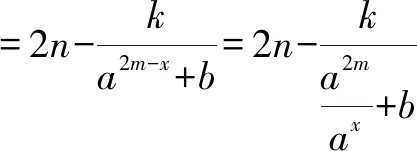
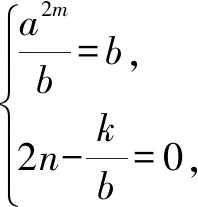
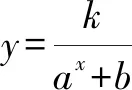
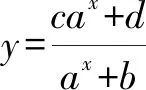
3.2 利用奇偶性的引申結論
人教版教材必修一第87頁有如下結論:函數y=f(x)的圖象關于坐標原點成中心對稱圖形的充要條件是函數y=f(x)為奇函數,可以將其推廣為:函數y=f(x)的圖象關于點P(a,b)成中心對稱圖形的充要條件是函數y=f(x+a)-b為奇函數.
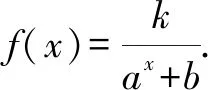
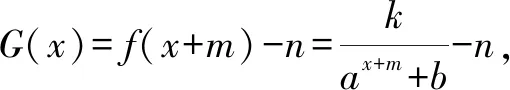
G(-x)=f(-x+m)-n
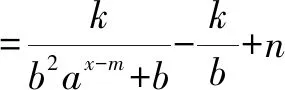
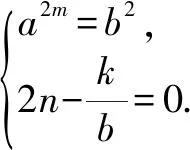
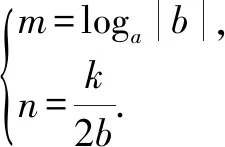
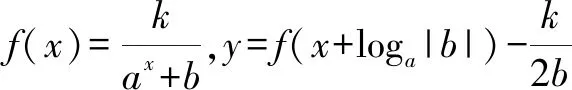
反之亦成立.
3.3 指數型分式函數的圖象特點
(1)b>0
若b>0,則函數y=f(x)的定義域為R,且ax+b>b.
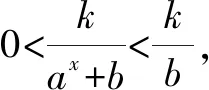
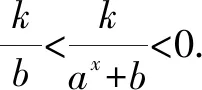
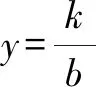
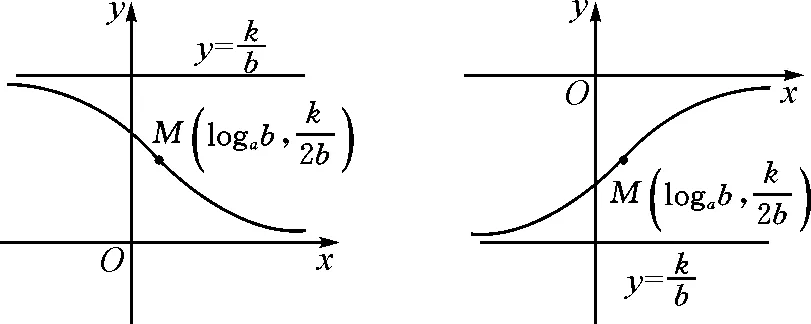
圖1
(2)b<0
若b<0,則函數y=f(x)的定義域為{x|x≠loga|b|},且ax+b≠0.
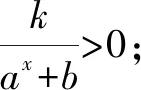
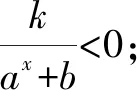
如圖2,f(x)的圖象類似于反比例函數的圖象.
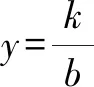
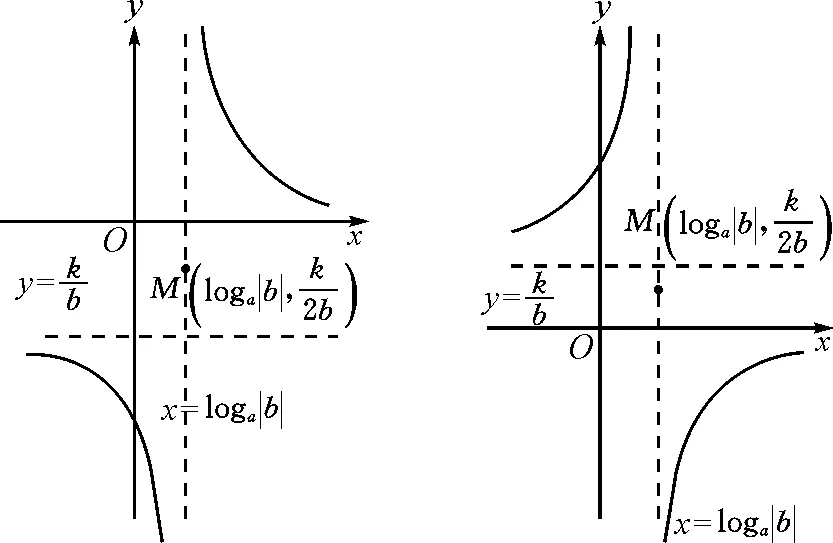
圖2
(3)函數值之間的關系
4 問題的應用
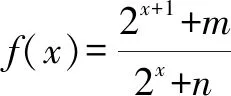
解析:f(x)是奇函數,則圖象關于原點中心對稱.如前所述,log2n=0,得n=1.又f(0)=0,則m=-2.
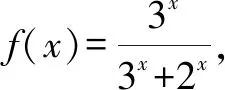
A.(-∞,1) B. (1,+∞)
C.(-∞,1)∪(1,+∞) D.(0,1)
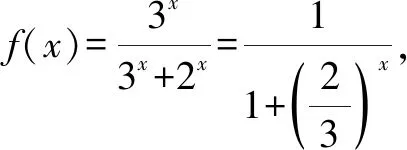
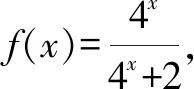
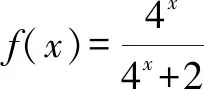
倒序得
兩式相加,得2S=2 020.故S=1 010.
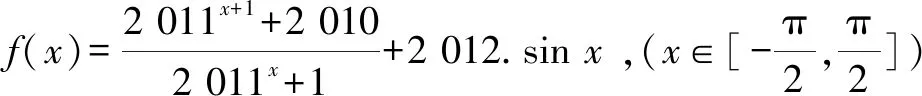
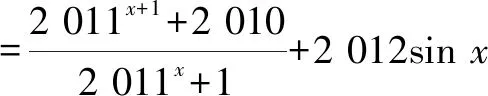
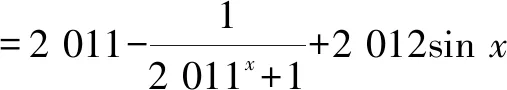
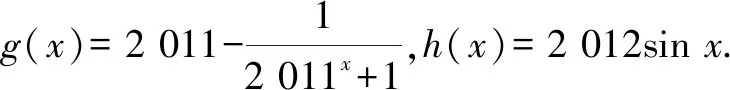
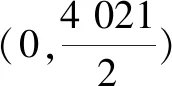
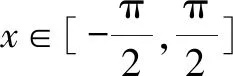
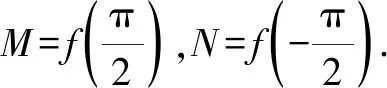
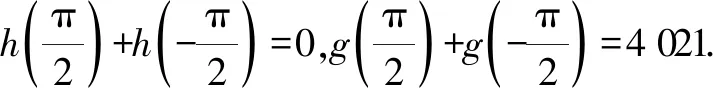
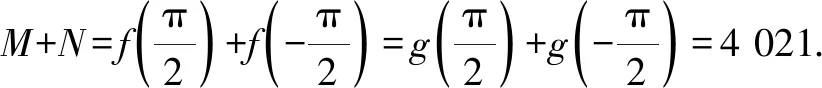
總之,以上內容最大限度地挖掘了教材中函數奇偶性在研究函數圖象對稱性上的應用,并對指數型分式函數模型的圖象特點作了深入全面的研究,挖掘了教材內涵.Z
猜你喜歡
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
新世紀智能(英語備考)(2021年10期)2022-01-18 05:12:14
新世紀智能(英語備考)(2021年9期)2021-12-06 05:22:38
新世紀智能(英語備考)(2021年11期)2021-03-08 01:10:02
中等數學(2021年11期)2021-02-12 05:11:46
新世紀智能(英語備考)(2020年11期)2021-01-04 00:41:50
新世紀智能(英語備考)(2020年6期)2020-08-14 01:06:24
新世紀智能(英語備考)(2020年12期)2020-04-13 00:50:42
今日農業(2019年14期)2019-09-18 01:21:42
快樂語文(2018年13期)2018-06-11 01:18:16

