正四棱錐創設,創新情境應用
——基于一道教材習題的探究
陳瑞霞
中國核工業集團公司二○二廠中學
立體幾何中的邊、角、面積或體積等要素的取值范圍或最值問題,一直是高考中立體幾何部分知識考查的一個熱點與創新點,融入立體幾何中的“動”與“靜”的對立與統一,“數”與“形”的綜合與轉化,數學知識、數學能力與核心素養等方面的考查得以全面兼顧,倍受關注.此類問題經常通過對高中數學教材中的例(習)題進行重新加工,借助問題背景包裝,空間幾何體建立,條件或結論的變換等多種方式,創新應用,看似平常,實則蘊含很多值得好好品味的東西.
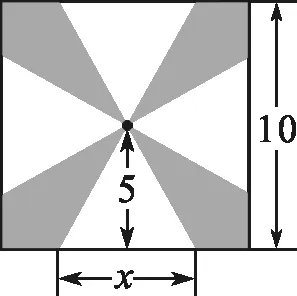
圖1
1 源于教材
習題(人民教育出版社2019年國家教材委員會專家委員會審核通過的《數學(必修第二冊A版)》第八章“立體幾何初步”中復習參考題8第169頁第4題)如圖1,一塊邊長為10 cm的正方形鐵皮上有四塊陰影.將這些陰影部分裁下來,然后用余下的四個全等的等腰三角形加工成一個正四棱錐形容器,把容器的容積V(單位:cm3)表示為x(單位:cm)的函數.
俗話說得好:鐵打的營盤流水的兵.高考中考查不變的是數學知識、數學思想方法與數學技巧等,變化的是問題情境的呈現方式以及問題的結構形式,以及設問的視角等.這就要求我們立足并深耕高中數學教材中的知識與例(習)題,學會突破常規,陳題巧改編,“舊瓶”裝“新酒”.
2 鏈接高考
在強調高考命題改革與創新的背景下,通過對高中數學教材中的例(習)題進行改編、組合、深入、創新等手段來賦予課本例(習)題新的面貌、新的生命,已經成為高考數學命題的一種新趨勢、新風尚.
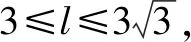
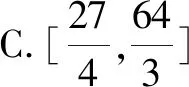
分析:該高考真題以課本例(習)題中的正四棱錐為背景,以及把該正四棱錐的體積表示為某個變量的函數,合理添加四棱錐的外接球這個創新場景,在原課本例(習)題的基礎上,增加難度與廣度,綜合考查空間幾何體之間的位置關系、體積以及導數法或均值不等式等,實現問題的變式、拓展與創新.
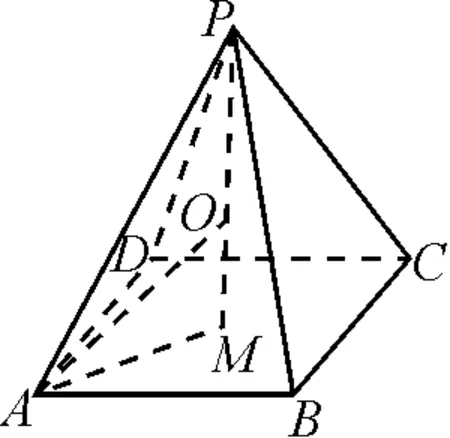
圖2
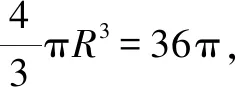
設PM=h,AM=a,則(h-3)2+a2=9,且l2=h2+a2∈[9,27].
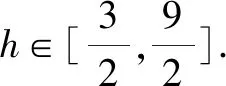
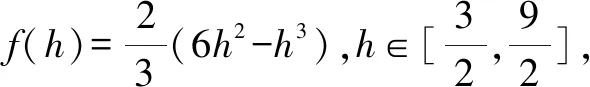
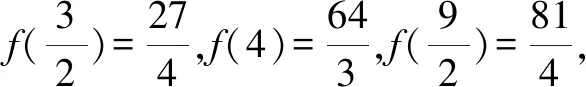
故選擇答案:C.
點評:具體設參時,可以以正四棱錐的高為變量,以正四棱錐的側棱長為變量,或以正四棱錐的側長與高所對應的角為變量,都可以合理構建對應的函數關系式,進而利用導數法或均值不等式法來確定對應的最值問題,實現問題的突破與解決.
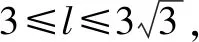
答案:C.
3 場景創新
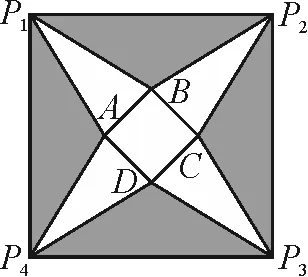
圖3
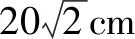
分析:以不同的方式顯現正四棱錐,通過底面正方形邊長的設置,結合正四棱錐的高的求解來確定其參數的取值范圍,進而確定邊長AB的取值范圍;結合正四棱錐的體積的表達式的構建,利用函數的設置與導數來確定其最值,進而得以確定此時邊長AB的值.
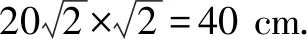
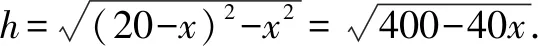
由400-40x>0,解得x<10,所以邊長AB的取值范圍為(0,20).
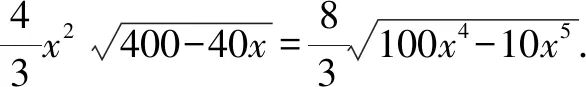
設函數f(x)=100x4-10x5(0 所以當0 所以當x=8時,f(x)取得極大值也為最大值,此時AB=16 (cm). 故填答案:(0,20);16. 點評:通過不同形式的正四棱錐的構建來創設問題場景,結合正四棱錐的體積與對應變量的關系,利用導數法或均值不等式法等來確定對應的最值,以不同的方式、相同的考點巧妙設置. 圖4 例3[2023屆河北省唐山市高三(上)摸底數學試卷]如圖4,一塊邊長為8的正方形鐵片上有四塊全等的陰影部分.將空白部分剪掉,對余下陰影部分按下面工序加工成一個正四棱錐:將四塊陰影部分分別沿虛線折疊,以其中等腰直角三角形組成棱錐的底面,余下為棱錐的側面.則所得正四棱錐的外接球表面積是( ). 分析:以不同的方式顯現正四棱錐,利用正四棱錐的確定以及與之對應的外接球的聯系,進而求解對應正四棱錐的外接球的表面積,從另一個視角來探究與應用. 圖5 解析:依題意可得如圖5所示的正四棱錐P-ABCD.設點O為正方形ABCD的中心. 連接PO,則PO⊥平面ABCD. 因為OA?平面ABCD,所以PO⊥OA. 故選擇答案:C. 點評:通過不同形式的正四棱錐的構建來創設問題場景,結合正四棱錐與其外接球的結構特征來構建兩者之間的關系,為相關參數的確定與求解提供條件,從問題場景的設置與空間幾何體的聯系等視角來創新與應用. 近幾年新高考數學中立體幾何試題的命制,呈現越來越靈活多變,形式越來越新穎多樣,但萬變不離其宗,大多數高考試題都可以在教材中追根溯源,尋覓其影蹤,找到其原型.因而,在高考復習備考過程中,全面回歸教材,注意對課本中典型例(習)題的練習與變式訓練,理解其內涵,規范其步驟,把握其實質,掌握其規律,真正做到胸有成竹,“胸中有本”.Z