回歸函數(shù)本質,提升數(shù)學能力
陶虹萍
廣西防城港市高級中學
函數(shù)是高中數(shù)學的重要基礎知識,貫穿于整個高中數(shù)學體系,是歷年高考數(shù)學的一個重要考點.在高考數(shù)學試卷中,涉及函數(shù)的知識往往以“2+1”(兩個小題,一個大題)的形式考查,一般占分為20分及以上,“函(數(shù))”概重點知識,“導(數(shù))”向高考的命題趨勢與考查熱點.破解涉及函數(shù)的高考試題,一定要正確回歸函數(shù)本質,讓學生學會從最基本的函數(shù)概念出發(fā)去理解數(shù)學問題,根據(jù)函數(shù)性質與數(shù)學運算去推理、演算、論證,結合數(shù)學思維去思考與分析問題,借助相應的技巧方法去解決函數(shù)問題,利用相關的數(shù)學知識來綜合與應用.
1 關注函數(shù)概念,回歸數(shù)學本源
函數(shù)概念是函數(shù)的本質屬性,涉及函數(shù)概念的問題也是高考中比較常見的一類題型,其破解的實質就是回歸數(shù)學本源,通過相關函數(shù)概念建立聯(lián)系,構建方程、不等式等來合理解決.
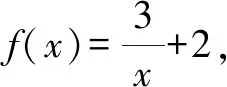
分析:結合題目條件,要求解反函數(shù)中的函數(shù)值問題,利用反函數(shù)的概念,即求解原函數(shù)中對應的函數(shù)值即可.
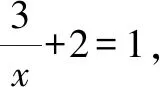
故填答案:-3.
點評:在破解一些函數(shù)的相關問題中,經(jīng)常要合理關注函數(shù)的基本概念,切實回歸數(shù)學基礎,從根源上切入數(shù)學問題的實質,回歸數(shù)學本源,合理建立相應的聯(lián)立,構建對應的方程、關系式等,進而得以合理解決.
2 關注函數(shù)求值,回歸數(shù)學基礎
函數(shù)求值問題往往以形式多樣的題型在高考試卷中出現(xiàn),或分段函數(shù),或實際應用,或融合交匯.剖析函數(shù)問題的本質,結合函數(shù)求值,回歸數(shù)學基礎,合理構建聯(lián)系,巧妙破解涉及函數(shù)求值的數(shù)學問題.
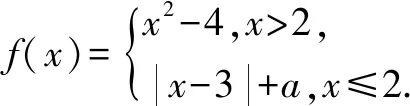
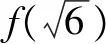
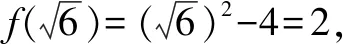
故填答案:2.
點評:對于分段函數(shù)的求值與應用問題,解題的關鍵就是回歸數(shù)學基礎,根據(jù)自變量的值所對應的解析式加以“對號入座”或分類討論,建立相應的聯(lián)系以及對應的關系式,合理構建,巧妙轉化.
3 關注函數(shù)性質,回歸數(shù)學內(nèi)涵
函數(shù)性質是歷年高考數(shù)學試卷中最常見、最基本的考點,通過函數(shù)的單調(diào)性、奇偶性、周期性等基本性質,或顯性表現(xiàn),或隱性包含,充分挖掘與應用函數(shù)的基本性質,回歸數(shù)學內(nèi)涵,巧妙破解數(shù)學問題.
例3(2021年高考數(shù)學新高考Ⅰ卷第13題)已知函數(shù)f(x)=x3(a·2x-2-x)是偶函數(shù),則a=______.
分析:通過函數(shù)基本性質的應用,借助函數(shù)奇偶性的相互轉化,把偶函數(shù)轉化為奇函數(shù),利用奇函數(shù)的性質代入應用,進而確定對應的參數(shù)值.
解析:由于函數(shù)f(x)=x3(a·2x-2-x)是偶函數(shù),而y=x3為R上的奇函數(shù),利用函數(shù)的基本性質,可知y=a·2x-2-x也為R上的奇函數(shù).
借助奇函數(shù)的性質,可得a·20-20=a-1=0,解得a=1.
故填答案:1.
點評:熟練利用函數(shù)的基本性質,巧妙將條件中涉及函數(shù)解析式的問題進行拆分或組合,合理轉化并應用函數(shù)的基本性質,從而達到巧妙解決函數(shù)問題的目的.
4 關注數(shù)學運算,回歸數(shù)學規(guī)則
數(shù)學運算是函數(shù)問題中最基本的數(shù)學規(guī)則,借助冪指數(shù)運算、對數(shù)運算等運算法則與應用,合理“串聯(lián)”起函數(shù)的相關基本知識,或直接利用函數(shù)應用,或交匯融合其他知識,得以合理應用,巧妙破解.

A.-1 B.lg 7
C.1 D.log710
分析:通過剖析題目條件,將給出的指數(shù)式進行對數(shù)化處理,然后合理分離參數(shù),巧妙代入所求的代數(shù)式,結合對數(shù)運算與合理變形來進行有效地化簡與求解.
解析:由條件2a=5b=10,兩邊同時取常用對數(shù),可得alg 2=lg 10=1,blg 5=lg 10=1.
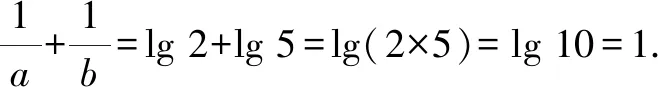
故選擇答案:C.
點評:在函數(shù)問題中,冪指數(shù)、對數(shù)等基本運算是最常見的一些基本數(shù)學運算,破解此類運算問題,巧妙同底化處理,指(數(shù))對(數(shù))互化,冪運算與對數(shù)運算法則等都是必須熟練掌握的基本數(shù)學規(guī)則.
5 關注技巧方法,回歸數(shù)學應用
技巧方法是破解函數(shù)問題比較特殊的一類策略,借助一些函數(shù)問題中的基本技巧方法,可以更加簡單快捷地處理涉及函數(shù)的相關問題.比如,利用特殊值確定函數(shù)的大致圖象,借助特殊函數(shù)的構建來確定函數(shù)的基本性質,等等.
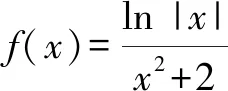
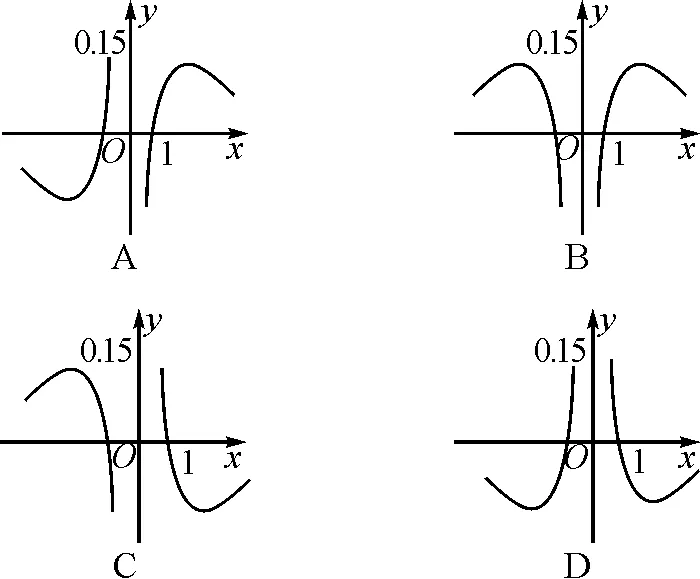
圖1
分析:結合條件中給出的函數(shù)解析式,先通過確定其定義域,結合奇偶性的定義判斷函數(shù)圖象的對稱性,再結合自變量的取值情況加以分類討論確定其函數(shù)值的正負情況,從而得以確定函數(shù)圖象的大致情況.
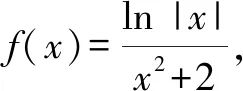
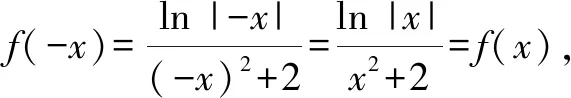
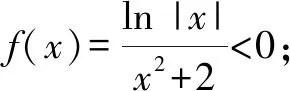
故選擇答案:B.
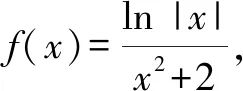
故選擇答案:B.
點評:借助常規(guī)方法,結合函數(shù)解析式,從定義域、函數(shù)性質、函數(shù)值等角度切入,對比分析,合理排除,正確破解.而借助特殊值代入,通過特殊值所對應的函數(shù)值的正負情況,直接加以排除,從而得以巧妙判斷,更快更簡捷.
回歸函數(shù)本質,從函數(shù)概念、函數(shù)性質、數(shù)學運算、技巧方法等思維視角切入,有效培養(yǎng)、形成、發(fā)展和拓展解題思維與方法,形成正確分析問題與解決問題的能力,從而簡捷快速解題,提高解題效率,提升數(shù)學能力,培養(yǎng)數(shù)學核心素養(yǎng).Z

