開展深度學習 提高學習效率

張隆傳

浙江省寧波市姜山中學

在素質教育的影響下，高中數學課堂的教學模式、教學手段、教學評價都發生了重大變革，并取得較好效果.但還存在一些問題，“題海戰術”依然是高三數學復習的主旋律.不可否認，“題海戰術”也能讓學生獲得一些收益，在一定程度上可以提升解題速度和解題信心，但題海無邊，如果不進行反思和總結，每天只是埋頭苦干，不僅學得苦，而且收獲甚微.對于教師亦是如此，課上講，課下批，將大多數的時間和精力都用于評講上，占用了對學生進行個體化分析的時間，為此“因材施教”的教學方針將難以有效實施.可見，這是一種“高耗能”的學習模式，不利于高三復習效率的提高.

那么如何變“高耗能”為“高收益”呢？筆者認為在高中數學教學中，尤其在高三復習階段，要引導學生進行深度學習.所謂深度學習就是打破“就題論題”式的表面化學習狀態，深入問題的本質進行分析，從本質和思想上深層建構，使學生在解決一個問題的基礎上可以理解并掌握解決一類題的思想和方法，進而提升學習效率.為了開展深度學習，教師要從學生的認知出發，精挑細選一些具有代表性和挑戰性的學習主題，讓學生積極參與，并全身心地投入到整個學習過程中.在此過程中通過思考、交流、合作等有意義的學習活動，掌握核心知識，提煉出重要的思想方法，從而在獲得成功體驗的同時，歸納總結出有價值的東西來，以此激發學生的內在學習動機，使學習更具方向性和目的性，讓學生在提升“四基”的基礎上，形成積極的態度和正確的價值觀，進而在提升學習效率的基礎上，培養學生的合作意識和創新精神，讓學習變得既高效又有意義.

那么在高三復習階段應該如何開展深度學習呢？筆者結合教學經驗，下面談幾點培養深度學習的策略，僅供參考！

1 重基礎，通概念

數學概念是數學學習的核心，是對數學對象本質屬性的直接表述，是開展深度學習的基礎.在開展深度學習時必須重視對概念、定理等基礎知識的梳理，這是達成理解的必要條件.但是在高三復習階段，部分教師常忽視基礎知識的再學習和再梳理，將教學的重心放在難題和新題上，片面認為學生只要難題會了，簡單的問題自然就通了.然而學生沒有扎實的基礎，導致難以理解題目的本質，在解題時常生搬硬套，不僅沒有提升解題能力，而且影響了解題信心，得不償失.同時，也有部分教師為了完成教學任務，追求課堂容量，教師主導課堂，學生的主體作用難以發揮，為了追趕教師的節奏，學生忙于解題，對基礎知識的再學習時間很少，為此也不利于“四基”的鞏固，不利于學生認知體系的完善.要知道，一道真正有意義的題目并不是因為它有多難、多新，而是通過這道題可以讓學生認清問題的本質，掌握解決問題的通法；同時，通過挖掘問題的各個方面引導學生建構完善的認知體系，從而通過一道題輻射到一類題，進而達到會一題通一類的效果.這樣可以幫助學生脫離“題海”，避免重復性練習所帶來的思維定式和思維疲勞，讓學生有時間和精力投入到更有意義的學習中去.

例1已知定義在R上的奇函數y=f(x)滿足f(2+x)=f(2-x)，當-2≤x<0時，f(x)=2x，則f(2 013)=.

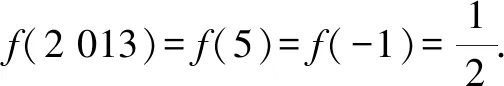
題目講解后，教師發現很多學生仍然露出疑惑的表情，為此決定“小題大做”，對問題進行深入剖析.

師：這是一道典型的考查函數對稱性和周期性的問題，現在一起復習一下與之相關的概念.(在教師的帶領下，學生復習了軸對稱和中心對稱的相關概念，又結合圖象重溫了函數周期性的相關應用.)

師：對于以上求解過程，你們認為哪一步是難點呢？

生1：函數的周期.

師：對于例1，你是如何判斷它的周期的呢？

生2：我是用圖象法.(教師讓學生在黑板上展示了畫圖過程.)

生3：圖象法是很直觀，但是畫圖需要的時間較長，可以直接應用函數的性質進行判定.

師：說說你的想法.

生3：因為y=f(x)為奇函數，所以f(2+x)=f(2-x)=-f(x-2)，由此可得f(x+4)=-f(x)，所以f(x+8)=-f(x+4)=-[-f(x)]=f(x)，由此可知f(x)的周期為8.

師：很好！借助“數”和“形”兩種方法得到了函數的周期，解決了這一難點后，問題也就迎刃而解了.

雖然帶領學生回顧基礎知識占用了較長的時間，但是通過細致的分析和回顧，學生不僅將本題學懂吃透了，而且對函數周期等問題又有了更深層的理解，其影響是深遠的.本題雖然難度不大，但若學生對相關基礎知識掌握不牢，要想順利求解也是較為困難的.所以在高三復習階段不能好高騖遠，要放低起點，通過緩坡讓學生思維螺旋上升，這樣既有助于夯實基礎，又能讓每個學生都有所收獲，讓他們的理解能力梯度上升.

2 重訓練，講方法

學習數學自然離不開解題，尤其學生運算能力的提升更是與平時的訓練息息相關.高考非常重視對學生運算能力的考查，運算能力的強弱很大程度上將直接影響高考的分數.那么運算能力應該如何提升呢？其實，運算能力并不是簡單的計算，其中還涉及觀察能力，總結歸納等綜合能力.為此，培養學生的運算能力時要重視基礎知識的積累，只有準確理解才不會因為理解偏差而出現錯解；同時要善于優化解題方法，進而有效避免復雜的運算過程，降低錯解的風險；另外要重視數學思想方法的科學指導，根據已知尋求更加快捷有效的解題途徑，以此來提升運算效率，提高解題準確率.

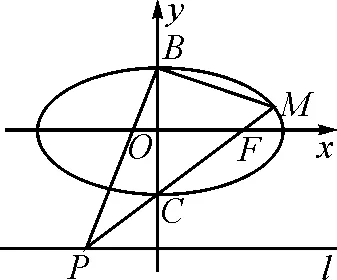
圖1

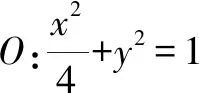
本題是一個綜合性較強的典型的動點問題，解題方案并不唯一.解題方案不同，其運算過程勢必也會不同.教師帶領學生從不同角度進行觀察和分析，尋找不同的解決方案，通過對運算過程及運算繁簡進行深度剖析，最終找到了最優解題方法.

在數學教學中不要急于求成，對于一些典型性問題要重點分析，引導學生通過多角度觀察和多維度探究來豐富解題經驗，同時將不同解題方案進行對比，尋求解決問題的通法和最優解決方案，以此來提升學生解決此類問題的運算能力.

3 重過程，促發展

在日常教學中為了追求效率，常出現“重結論、輕過程”的現象，忽視了對學生思維能力和自主學習能力的培養，使學生的解題思路過于保守和單一.其實，無論在新知授課，還是在例習題的講解中都要重視過程的分析，要充分暴露學生的思維過程，進而對暴露的問題進行引導和矯正，帶領學生走出思維的誤區.同時，只有經歷過程才能發現思維的“閃光點”，進而在鼓勵和引導下，培養學生的獨創力.

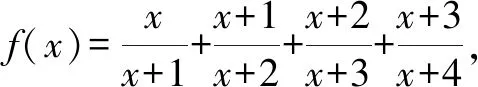
本題雖然有一定難度，但并不是完全不能求解.為此，教學過程中教師堅持“以生為主”，通過合作交流展示學生的思維過程，從而在過程中發現不足，在交流中共同提升.

師：很好，踏實的計算也是優秀的品質，平淡卻不平凡.你們還有其他的解決辦法嗎？

生2：已知條件中的函數表達式是有一定特點的，所求的值也是有規律的，求解時不應該急于代入，應該先找到內在聯系，挖掘內在規律，只是還沒有發現.

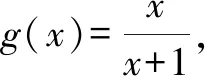
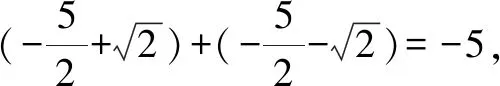
通過過程分析不僅準確地求得了答案，而且通過對特殊的挖掘揭示了問題的真面目，讓學生充分享受數學分析推理的樂趣，學生的分析能力.推理能力、運算能力也得到較大提升.

總之，若要提高高三復習效率，教師在教學中就需要對教學內容進行“深加工”，引導學生回歸問題的本質，通過對重要思想方法的提煉和總結，促進解題能力、思維能力全面提升.Z