多方法破解，多規(guī)律總結，多變式拓展
——對2021年數學新高考Ⅰ卷第5題的探究

鄧 杰

江蘇省海門中學

1 真題呈現

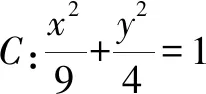
A.13 B.12 C.9 D.6

該題題目簡潔明了，通過橢圓標準方程的給出，進而確定橢圓兩焦半徑積的最大值.題目難度不大，破解思維方式多樣.破解最直接有效的辦法就是應用基本不等式；而采用兩點間距離公式或焦半徑公式也是不錯的方法，結合函數思維來確定最值；針對選擇題的特點，可直接利用極端思維來確定兩焦半徑積的兩個極端取值，進而得以合理判斷.不同的破解方法，展示不同的思維方式.

2 真題破解

方法1：基本不等式法.

解析：由于F1，F2是橢圓C的兩個焦點，則a=3，而點M在C上，利用橢圓的定義可得|MF1|+|MF2|=2a=6.

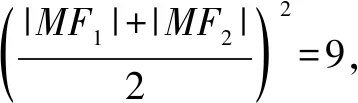
故選擇答案：C.

點評：根據橢圓的標準方程確定相應參數的值，利用橢圓的定義得到兩線段的長度之和，結合基本不等式即可確定兩線段長度積的最大值.結合橢圓的定義，借助基本不等式來確定關系式的最值，是破解此類問題中最常見的一種基本方法，思維直接，簡單快捷.

方法2：距離公式法.

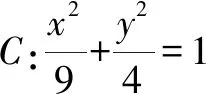
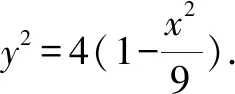
又|MF1|·|MF2|

當且僅當x=0時等號成立.

故選擇答案：C.

點評：根據橢圓的標準方程確定相應參數的值，設出動點M的坐標，利用兩點間的距離公式確定兩線段長度積的關系式，通過消參、等價變換，得到相應的二次函數，利用二次函數的圖象與性質來確定對應的最大值即可.通過距離公式來轉化線段的長度問題進而轉化為函數問題，利用函數的圖象與性質來確定最值,是破解此類平面解析幾何相關問題的常用方法.

方法3：焦半徑公式法.

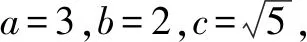
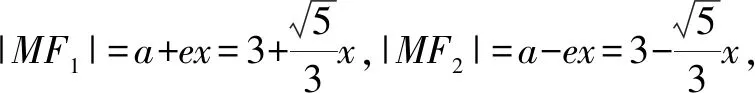
故選:C.

點評：根據橢圓的標準方程確定相應參數的值，并求得橢圓的離心率，設出動點M的坐標，結合橢圓的焦半徑公式分別確定|MF1|與|MF2|的表達式，進而確定兩線段長度的積關系式，得到相應的二次函數，利用二次函數的圖象與性質來確定對應的最大值即可.焦半徑公式是圓錐曲線中的拓展與提升，是破解與焦半徑有關問題的基本方法.

方法4：極端思維法.

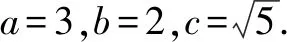
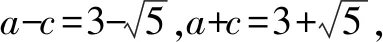
當動點M與短軸的頂點重合時，|MF1|,|MF2|的值均為a=3，此時|MF1|·|MF2|=9.

所以|MF1|·|MF2|的最大值為9.故選C.

點評：根據橢圓的標準方程確定相應參數的值，結合橢圓圖形的對稱性，借助極端思維，利用動點M與橢圓長軸的頂點、短軸的頂點重合時，對應的線段長度以及兩線段長度的積，通過比較來判斷相應的最大值問題.極端思維在解決平面解析幾何中的相關問題時，以極端的特殊思維來解決，極具可行性.

3 規(guī)律總結

根據以上高考真題及其對應的破解過程，特別是方法2～4，除了確定相應的最大值外，還可以確定相應的最小值問題.參照以上破解方法，總結規(guī)律，可以得到以下幾個相應的一般性結論.

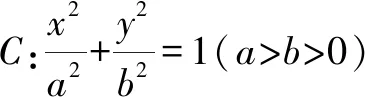
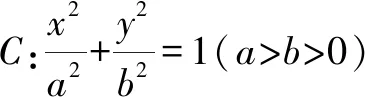
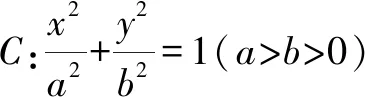
結論的證明，可以直接參照以上高考真題的破解方法2～4中的過程，具體加以實際分析即可，這里不多加贅述.

4 變式拓展

保留題目條件，改變所要求解的關系式，變原來“兩焦半徑的積”為“兩焦半徑的平方和”，可以得到以下兩個對應的變式.

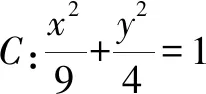
A.28 B.24 C.18 D.12

解析：由于F1，F2是橢圓C的兩個焦點，則a=3.而點M在C上，利用橢圓的定義可得|MF1|+|MF2|=2a=6.

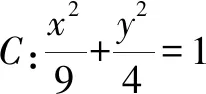
A.28 B.24 C.18 D.12

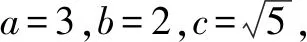
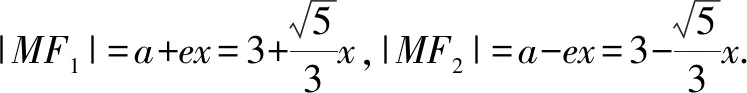
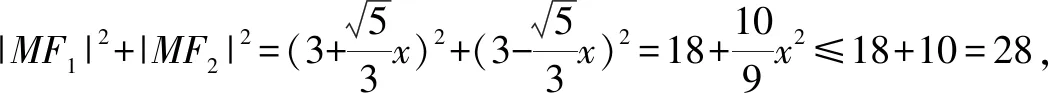
當然，融合變式1與變式2的結論，又可以進一步得到確定橢圓的兩焦半徑的平方和的取值范圍問題，這里就不另展示.

5 教學啟示

(1)研究高考典型真題不能只以難題為標準

歷年高考過后，都會有很多的教師去研究一些高考典型真題，基本上選擇一些選擇題、填空題或解答題的壓軸題之類的難題來研究，這樣固然可以挖掘問題本質，突破問題的難點.但對大部分學生而言，基本題與基本方法才是根本，因而一些簡單題也是研究的一大方向，不能掉以輕心.

(2)研究一題必有所得

深入研究一些基本的高考典型真題，從問題的類型、出題的落腳點、問題的知識點、切入的突破點等方面，都可以得到很好的體會，進而不斷發(fā)展解題思維，展示解題方法，總結解題規(guī)律，探究變式拓展，引領并指導學生跳出題海，提升數學品質，提高數學能力，培養(yǎng)數學核心素養(yǎng).Z