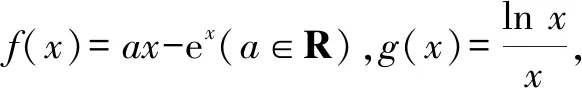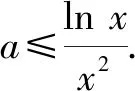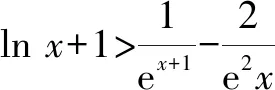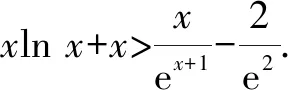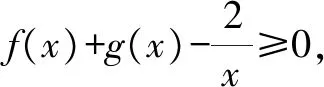淺探“任意性”或“存在性”問題的解法
徐清杰
山東省惠民縣第一中學
近幾年來,高考數(shù)學試題及各省市模擬題中,含邏輯量詞的“任意性”或“存在性”問題多有出現(xiàn),涉及此類問題,學生們多有困惑,現(xiàn)結合個人的教學體會,將其整理歸納為五種情形,與大家共同探討此類問題的解法,以便于今后的學習實踐.
1 一個“任意”、一個“存在”,兩個不同函數(shù)
此類試題的特點是含有一個“任意”和一個“存在”,分屬兩個不同的變量,來自兩個不同的范圍(有時兩個范圍也可以相同),分別針對兩個不同的函數(shù).
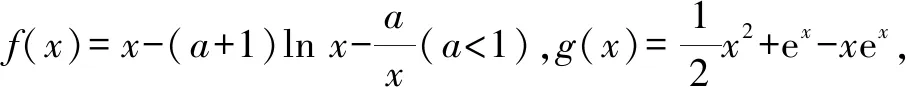
分析:題中的“存在”“任意”等價于:f(x)中至少存在一個x0使得f(x0)小于g(x)值域中的任意一個實數(shù),即f(x)min 歸納:(1)?x1∈D1,?x2∈D2,f(x1)≥g(x2)成立,則f(x)min≥g(x)min.(適用于f(x),g(x)最值存在的情況,以下同.) 剖析:① 若f(x)的最小值不存在,f(x)∈(m,n),則m≥g(x)min;②若g(x)的最小值不存在,g(x)∈(m′,n′),則f(x)min>m′;③若f(x),g(x)的最小值同時不存在,則m>m′.(注:若f(x),g(x)的最小值不存在時,可以用其值域的左端點替代,但需要驗證等號是否能取到.) (2)若?x1∈D1,?x2∈D2,f(x1)≤g(x2)成立,則f(x)max≤g(x)max. 剖析:若f(x),g(x)的最大值不存在時,可以用其值域的右端點替代,同樣需要驗證等號是否能取到,情況與上述剖析類似,不再一一闡述. (3)若?x1∈D1,?x2∈D2,f(x1)=g(x2),則f(x)的值域是g(x)的值域的子集. 此類試題的特點是含有兩個“任意”,分屬兩個不同的變量,來自兩個不同的范圍(有時兩個范圍也可以相同),分別針對兩個不同的函數(shù). 分析:題中兩個“任意”,說明f(x)的值域中任意一個實數(shù)都不小于g(x)值域中任意一個實數(shù),即f(x)min≥g(x)max. 故a的取值范圍為[1,+∞). 歸納:(1)若?x1∈D1,?x2∈D2,f(x1)≥g(x2)成立,則f(x)min≥g(x)max. (2)若?x1∈D1,?x2∈D2,f(x1)≤g(x2)成立,則f(x)max≤g(x)min. 此類試題的特點是含有兩個“存在”,分屬兩個不同的變量,來自兩個不同的范圍(有時兩個范圍也可以相同),分別針對兩個不同的函數(shù). 故a的取值范圍為(-2,0). 歸納:(1)若?x1∈D1,?x2∈D2,f(x1)≥g(x2),則f(x)max≥g(x)min. (2)若?x1∈D1,?x2∈D2,f(x1)≤g(x2),則f(x)min≤g(x)max. (3)若?x1∈D1,當x2∈D2,f(x1)=g(x2),則f(x)的值域與g(x)的值域的交集是非空集. 點評:此類兩個不同的x值,滿足兩個不同函數(shù)的求參數(shù)范圍問題,通常有兩種解法.①求出兩邊各自的最值,再解兩最值的不等式,如例1、例3;②有時一邊的最值不易求出,而另一邊的最值容易求出時,可借助于求出的最值,對不等式進行同解變形,構造一個與背景函數(shù)相關的輔助新函數(shù),再將不等式分離參數(shù),如例2;也可對參數(shù)進行分類討論. 此類試題的特點是含有一個“任意”,連接一個變量,分別針對兩個不同的函數(shù). 例4已知函數(shù)f(x)=ex-1,g(x)=ax2+x,若對任意x∈[0,+∞),f(x)≥g(x)恒成立,求實數(shù)a的取值范圍. 分析:可先考慮分離參數(shù)法;如果參數(shù)不易分離,再考慮構造新函數(shù)法,即?x∈[0,+∞),f(x)-g(x)≥0恒成立,令h(x)=f(x)-g(x),只需h(x)min≥0即可. 歸納:(1)若?x∈D,f(x)≥g(x)恒成立,可先考慮分離參數(shù)法;后考慮構造新函數(shù)法,設h(x)=f(x)-g(x),則h(x)min≥0. (2)若?x∈D,f(x)≤g(x),解法同上(或分離參數(shù)法;或h(x)max≤0). 此類試題的特點是含有一個“存在”,連接一個變量,分別針對兩個不同的函數(shù). 分析:可以先考慮分離參數(shù)法解決問題;如果不易分離參數(shù),可直接轉化為?x∈(0,+∞),f(x)-g(x)+ex≤0成立,令h(x)=f(x)-g(x)+ex,則只需證明h(x)min≤0. 歸納:(1)若?x∈D,f(x)≥g(x)成立,可先考慮分離參數(shù)法;后考慮構造新函數(shù)法,設h(x)=f(x)-g(x),則h(x)max≥0. (2)若?x∈D,f(x)≤g(x),解法同上(或分離參數(shù)法;或h(x)min≤0). 點評:此類一個x值,滿足兩個不同函數(shù)的問題,若條件中含有參數(shù),需要求參數(shù)的取值范圍時,可考慮兩種解法.①若參數(shù)容易分離,可將參數(shù)與其他變量分離,構造一個新函數(shù),轉變?yōu)榍笮潞瘮?shù)的最值,如例5;②若參數(shù)不易分離,可通過不等式的同解變形,構造一個與背景函數(shù)相關的新函數(shù),常需對參數(shù)進行分類討論,如例4.若證明不等式成立時,通常也有兩種證明方法.一是通過不等式的同解變形,將不等式轉化為兩個函數(shù)的最值進行比較,如例6;二是通過不等式的同解變形,構造一個新函數(shù)證明不等式,如例7. 總結:兩個不同的x值x1,x2針對兩個不同的函數(shù)f(x1),g(x2)的“任意性”或“存在性”問題,根據(jù)上述兩個不同x值的不同情況,分別求出f(x),g(x)相應的最值,然后比較大小;有時也會只求一個函數(shù)的最值,重新加以整合,或分離參數(shù)法,或構造一個新函數(shù)進行分類討論.同一個x值針對兩個不同的函數(shù)f(x),g(x)的“任意性”或“存在性”問題,根據(jù)上述同一個x值的不同情況,或分離參數(shù)法,或構造一個關于f(x),g(x)差的新函數(shù),再求相應的最值.Z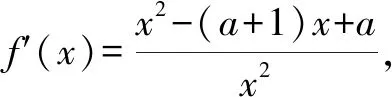
2 兩個“任意”,兩個不同函數(shù)
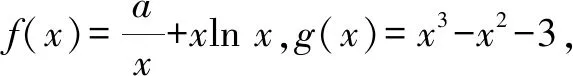
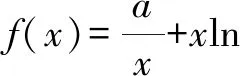
3 兩個“存在”,兩個不同函數(shù)
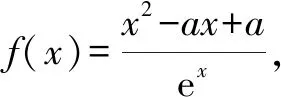
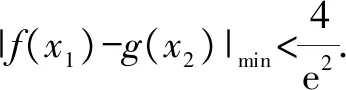
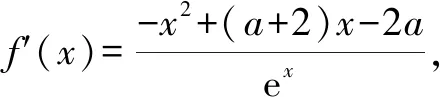
4 一個“任意”,兩個不同函數(shù)
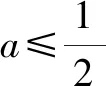
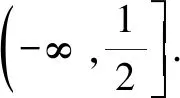
5 一個“存在”,兩個不同函數(shù)