利用均值不等式求函數最值的六種方法
2023-02-11 03:35:20洪家鳳
中學數學雜志 2023年1期
曹 昕 洪家鳳
安徽省渦陽縣第二中學 安徽省渦陽縣第四中學
均值不等式是高中數學的一個重要公式,常出現在填空、選擇題中,結合不等式的性質進行考查,部分大題解答過程中也常用到.下面結合實例給出求函數最值的6種方法.
1 整體代換法
在利用均值不等式求最值時常會遇到一些較復雜的運算,直接運算可能比較復雜甚至無法得出結果,而采用整體代換的方法.有時可以簡化運算.







2 取平方法


解:由2x-1和5-2x的和為定值,得
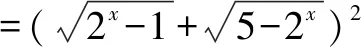
≤4+(2x-1)(5-2x)=8.


3 變量變換法



當t=0時,y=0.

4 湊系數法
湊系數是使用配湊法解題的一個重要思路,常用在形如y=x(a-bx)(a,b為常數)的函數求最值,只需要將x(a-bx)配湊成和為定值的式子,即在x前面配上一個系數b使bx+(a-bx)=a,從而使等式滿足求最值的條件進而解決問題.
例4當0 分析:在利用均值不等式求最值時,目標等式中需要滿足和或者積為一個定值.本題由已知條件0 解:y=x(8-2x) 當且僅當2x=8-2x時,上式等號成立. 即當x=2時,y=x(8-2x)的最大值為8. 解:因為x =-2+3=1, 所以當x=1時,函數f(x)的最大值為1. 所以,所求函數值域為(-∞,1]∪[9,+∞). 總而言之,利用均值不等式求解最值問題時,要熟練掌握變形技巧,積極地為利用均值不等式求解創造條件;要善于總結歸納解題方法,多加練習提高解題能力,提升利用均值不等式求最值問題的解題技巧.5 湊項法




6 分離法





猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
中等數學(2022年2期)2022-06-05 07:10:50
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34

